Mathématiques,
DNB Amérique du nord 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.. |
..
..
......
...
|
Exercice 1. 20 points
1. La moyenne des nombres suivants est :
12 ; 15 ; 10 ; 7 ; 13.
(12+15+10+7+13 ) / 5 =11,4. Affirmation A.
La médiane des prix est : 7 ; 10 ; 12 ; 13 ; 15.
2. Lors d'un entraînement un élève parcourt 20 m en 6 s.
Sa vitesse moyenne est : 20 / 6 ~3,33 m/s ou 3,33 x3,6 = 12 km / h.
3.
Une urne contient 15 boules indiscernables numérotées de 1 à 15.
l'espace sont affectés.
La probabilité de tirer au hasard une boule sur laquelle apparaît un nombre premier est :
Nombres premiers : 2 ; 3 ; 5 ; 7 ; 11 ; 13.
6 / 15.
4. Le triangle A'B'C' est l'image du triangle ABC par l'homothétie de centre O et de rapport (-3).
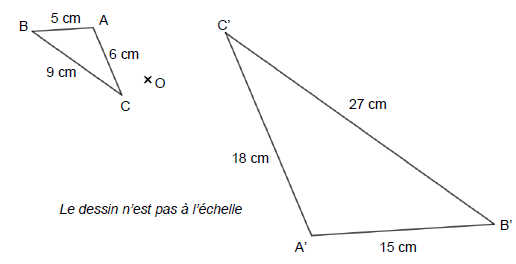
L’aire du triangle A’B’C’ est égale à 9 fois l’aire du triangle ABC.
Aire du triangle ABC = base x hauteur /2 ;
Chaque côté du triangle A'B'C' est égal à 3 fois le côté correspondant du triangle ABC.
Exercice 2. 20 points.
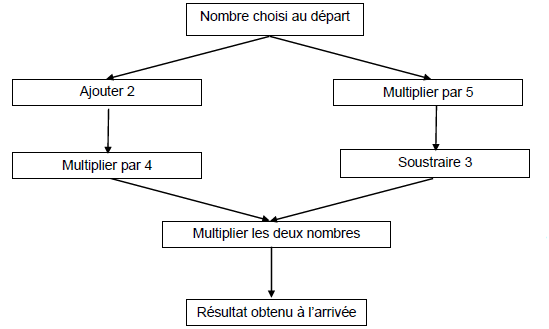
1) Montrer que si on choisit 2 comme nombre de départ, le résultat à l’arrivée est 112.
(2+2) x4 = 16 ; 2 x5-3=7 ; 16 x7 =112.
2) Quel est le résultat obtenu à l’arrivée quand on choisit −3 comme nombre de départ ?
(-3+2) x4 = -4 ; -3 x5-3=-18 ; -4 x(-18)=72.
3) On choisit 𝑥 comme nombre de départ.
Parmi les expressions suivantes, lesquelles permettent d’exprimer le
résultat à l’arrivée de ce programme de calcul. Aucune justification
n’est demandée.
(x+2)*4 et 5x-3 ; 4(x+2)(5x-3 )=4(5x2-3x+10x-6)=20x2+28x-24. Expressions C et D.
4) Trouver les deux nombres de départ qui permettent d’obtenir 0 à l’arrivée. Expliquer la démarche.
4(x+2)(5x-3) =0
x+2 = 0 ; x = -2.
et 5x-3 = 0 ; x = 3 /5.
5) Développer et réduire l’expression (4x+2)(5x-3) =20x2-12x+10x-6 =20x2-2x-6.
Exercice 3 : (20 points)
Un cinéma propose trois tarifs :
Tarif « Classique » : La personne paye chaque entrée 11 €.
Tarif « Essentiel » : La personne paye un abonnement annuel de 50 € puis chaque entrée coûte 5 €.
Tarif « Liberté » : La personne paye un abonnement annuel de 240 € avec un nombre d’entrées illimité.
1) Avec le tarif « Classique », une personne souhaite acheter trois entrées au cinéma. Combien va-t-elle payer ?
11 x3 = 33 €.
2) Avec le tarif « Essentiel », une personne souhaite aller huit fois au cinéma. Montrer qu’elle va payer 90 €.
50 +8 x5 = 90 €.
3) Dans la suite, 𝑥 désigne le nombre d’entrées au cinéma.
On considère les trois fonctions f, g et h suivantes :
Associer, sans justifier, chacune de ces fonctions au tarif correspondant.
f(x)= 50+5x ( tarif essentiel) ; g(x) =240 ( tarif liberté); h(x) =11x ( tarif classique).
Le graphique ci-dessous représente le prix à payer en fonction du nombre d’entrées pour chacun de ces trois tarifs.
La droite (d1) représente la fonction correspondant au tarif « Classique ».
La droite (d2) représente la fonction correspondant au tarif « Essentiel ».
La droite (d3) représente la fonction correspondant au tarif « Liberté ».
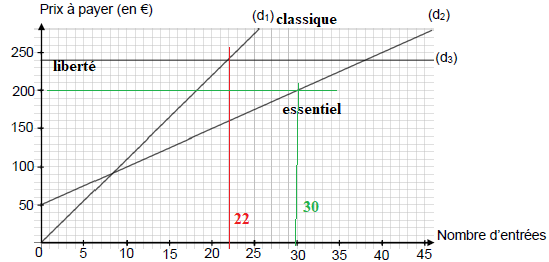
4) Quel tarif propose un prix proportionnel au nombre d’entrées ?
(d1) : tarif classique, droite passant par l'origine.
5) Pour les questions suivantes, aucune justification n’est attendue.
a. Avec 150 €, combien peut-on acheter d’entrées au maximum avec le tarif « Essentiel » ?
50 +5x = 150 ; 5x =100 ; x =20.
b. À partir de combien d’entrées, le tarif « Liberté » devient-il le tarif le plus intéressant ?
50+5x > 240 ; 5x >190 ; x > 38 ; 11 x > 240 ; x >240 / 11 ( environ 22).
c. Si on décide de ne pas dépasser un budget de 200 €, quel est le tarif qui permet d’acheter le plus grand nombre d’entrées
Tarif essentiel : 50 +5x = 200 ; 5x = 150 ; x = 30.
|
...
|
....
|
Exercice 4 : (21 points)
M. et Mme Martin veulent construire une terrasse en béton dans leur
jardin. Ils souhaitent que leur terrasse ait une hauteur de 15 cm. Les
représentations ci-dessous ne sont pas à l’échelle.
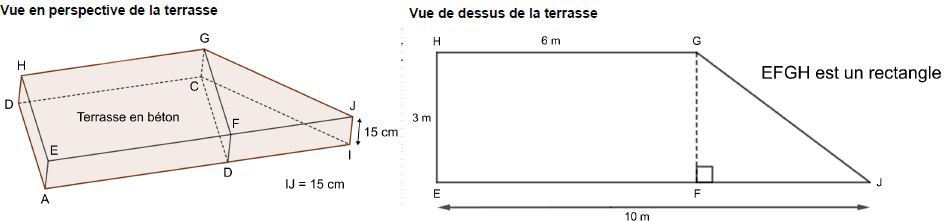
1) Montrer que FJ = 4 m.
EJ - HG = 10-6 = 4 m.
2) Afin de pouvoir couler le béton, M. et Mme Martin doivent délimiter
la terrasse en installant des planches tout autour. Quelle longueur de
planches doivent-ils acheter au minimum ?
Relation de Pythagore dans le triangle FGJ : GJ2 = 32 +42 =25 ; GJ = 5 m.
6 +5+3 +10=24 m.
3) M. et Mme Martin souhaitent réaliser 4 m3 de béton.
a. Montrer que le volume de la terrasse est bien inférieur à 4 m3.
Aire du rectangle 6 x3 = 18 m2 ; aire du triangle : 3 x4 / 2 = 6 m2 ; aire totale : 24 m2.
Volume de bton : 24 x0,15 =3,6 m3.
b. Sachant que pour faire 1 m3 de béton, il faut 250 kg de ciment, quelle masse de ciment (en kg) doivent-ils acheter pour réaliser 4 m3 de béton ?
250 x4 = 1000 kg.
c. Pour faire du béton, on ajoute de l’eau à un mélange de ciment, de gravier et de sable.
Dans ce mélange, les masses de ciment – gravier – sable sont dans le ratio 2 : 7 : 5.
Déterminer (en kg), la masse de gravier et la masse de sable nécessaires pour réaliser les 4 m3 de béton.
Masse de gravier : 1000 x7 / 2 =3500 kg.
Masse de sable : 1000 x5 / 2 =2500 kg.
4) M. et Mme Martin souhaitent peindre la surface supérieure de leur terrasse.
Déterminer le type et le nombre de pots nécessaires pour effectuer ces travaux avec un coût minimum.
Deux couches de peinture sont nécessaires.
1 litre de peinture permet de réaliser une couche de 5 m2.
2 x24 =48 m2 en deux couches soit 10 L de peinture.
Pot B : 129,90 €.
Premier pot A : 79,90 € ; deuxième pot A : 79,90 / 2 =39,95 €. Total :119,95 €.
Exercice 5 : (19 points)
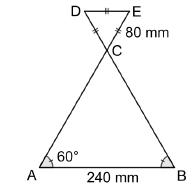
Dans cet exercice on considère la figure codée suivante.
Les points A, C et E sont alignés.
Les points B, C et D sont alignés.
AB = 240 mm ; CE = 80 mm.
Partie A
1) Montrer que le triangle ABC est équilatéral.
Les angles A et B sont égaux à 60°. La somme des angles d'un triangle vaut 180°. l'angle C mesure donc 60°.
Les trois angles sont égaux : le triangle ABC est équilatéral.
2) Montrer que les droites (DE) et (AB) sont parallèles.
Le triangle CDE est équilatéral ( 3 côtés égaux).
Réciproque de la propriété de Thalès :AB / DE = AC / CE = BC / CD.
Les droites (DE) et (AB) sont donc parallèles.
Partie B.
On donne le programme suivant qui permet de tracer la figure précédente. Ce programme comporte une variable nommée « côté ».
Les longueurs sont données en pas : 1 pas représente 1 mm.
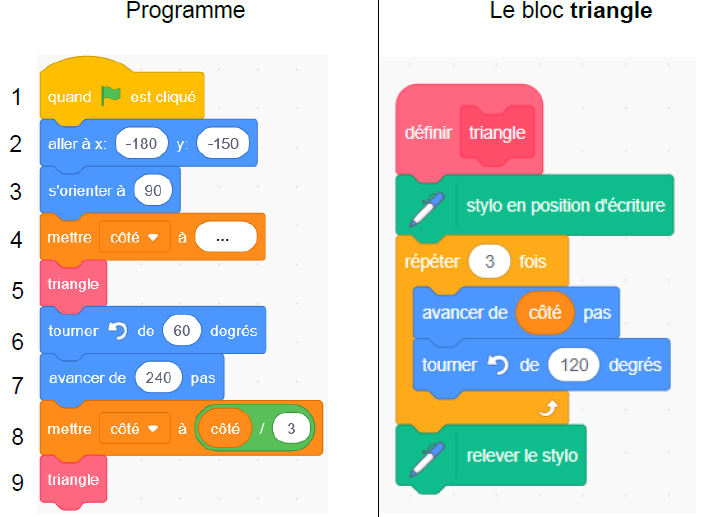
1) Quelles sont les coordonnées du point de départ du lutin ?
-180 ; -150.
2) Quelle valeur doit être saisie à la ligne 4 dans le programme ?
240.
3) Le lutin démarre à la case D8. Dans quelle case se trouve-t-il lorsqu’il vient d’exécuter la ligne 7 du programme ?
G3.
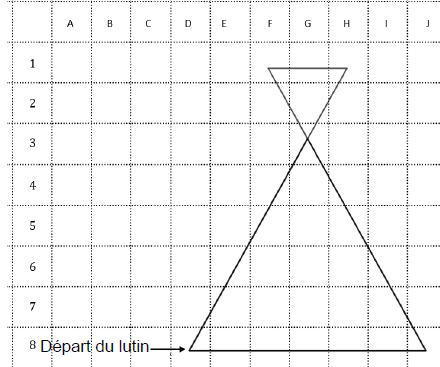
4) Expliquer l’instruction « côté / 3 » de la ligne 8 du programme pour le tracé de la figure.
Le petit triangle est l'image du triangle ABC par l'homothétie de centre C et de rapport 80 / 240 = 1 /3.
|
|
|
|
|