Mathématiques, DNB Amérique du sud 2024.

Exercice 1 (20 points)
1. Une urne contient trois jetons verts et deux jetons blancs. On tire un jeton au hasard.
Quelle est la probabilité d’obtenir un jeton blanc ?
2 cas favorables sur 5 possibilités : 2 /5.
2. Quelle est la vue de droite de ce solide ?

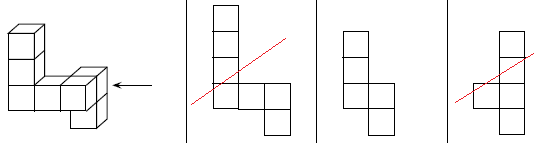3. B, H et A sont alignés.
B, D et C sont alignés.
BD = 2 cm ; BC = 10 cm ; AC = 16 cm; (DH) // (AC).
Quelle est la longueur du segment [DH] ?

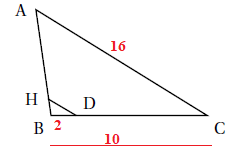
Relation de Thalès : HD / AC = BD / BC ; HD = 16 x 2 / 10 =3,2 cm.
4. Voici un engrenage :
12 dents 9 dents
Si la petite roue effectue exactement 4 tours complets, combien de tours complets effectue la grande roue ?

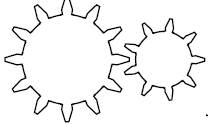
Quand la petite roue fait un tour, la grande tourne de 9 crans.
Quand la petite roue fait 4 tours, la grande tourne de 9 x4 =36 cran soit 3 tours.
4 x 9 /12=3 tours.
5. Le carré AGFE est l’image du carré ADCB par une homothétie de centre A.
Le triangle EGF est l’image d’un triangle par cette même homothétie.
Quel est ce triangle?

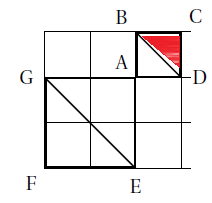
Homothétie de centre A et de rapport 2.
Exercice 2. 24 points.
On considère deux fonctions f et g définies par :
f (x) = x²−x −6 ; g(x) = −2x.
1. a. Montrer que l’image de 5 par la fonction f est 14.
f(5)= 5²-5-6=14.
b. Déterminer l’antécédent de 4 par la fonction g.
4 = -2x ; x = -4/2 = -2.
Pour calculer des images de nombres par les fonctions f et g, on utilise un tableur et on obtient la copie d’écran suivante :

	A	B	C	D	E	F	G	H
1	x	-4	-3	-2	-1	0	1	2
2	f(x)	14	6	0	-4	-6	-6	-4
3	g(x)	8	6	4	2	0	-2	-4

c. À l’aide des informations précédentes, citer deux antécédents de 14 par la fonction f .
-4 et 5.
d. Quelle formule a-t-on pu saisir dans la cellule B2 avant de l’étirer vers la droite jusqu’à la cellule H2 ?
=B1*B1-B1-6.
e. Existe-t-il un nombre qui a la même image par la fonction f et par la fonction g ?
-3 et 2.
2. a. Montrer que, pour tout nombre x, f (x) est égal à (x +2)(x −3).
On développe : (x +2)(x −3)=x²-3x+2x-6=x²-x-6.
b. Résoudre l’équation f (x) = 0.
x+2= ; x= -2.
x-3=0 ; x=3.
Exercice 3. 22 points.
1. Le tableau ci-dessous présente, pour quatre félins étudiés, les probabilités d’attraper leur proie quand ils la poursuivent.

Félin	Probabilité d'attraper la proie
lion	25 % ou 0,25
guépard	½ ou 0,5
tigre	0,1
chat	0,6

Vérifier que, parmi les quatre félins étudiés, le chat a la probabilité la plus élevée d’attraper sa proie quand il la poursuit.
2. Le plus souvent, le guépard est le félin le plus rapide avec une vitesse pouvant atteindre 115 km/h. À cette vitesse, en combien de secondes le guépard parcourt-il 100 mètres ?
115 x 1000 /3600=115 /3,6 ~31,94 m /s.
100 / 31;94 =3,13 s.
Dans un pays d’Afrique, on estimait à :
• 1 200 guépards en 1999.
• 170 guépards en 2016.
Dans ce pays, est-il vrai que le nombre de guépards a baissé d’environ 86% entre 1999 et 2016 ?
(1200 -170) / 1200 x 100 ~ 86 %. Vrai.
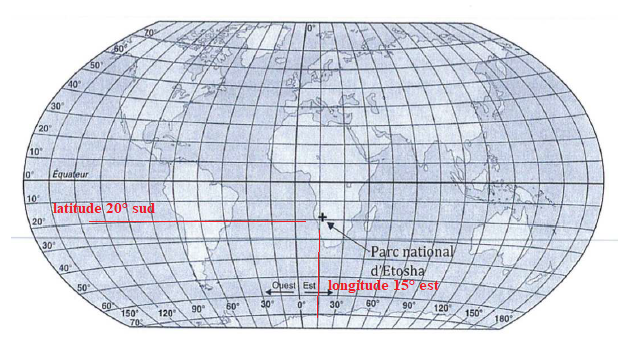
3. Dans le parc national d’Etosha enNamibie, on peut observer des lions et des guépards.
À l’aide de la carte ci-dessous, donner approximativement la latitude et la longitude du parc national d’Etosha.