Mathématiques, DNB Polynésie 2024 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1 QCM (20 points)   1. ABC est un triangle tel que AB = 20 0cm, BC = 21 cm et Ac = 29 cm. On peut affirmer que : AC2 = 292 =841. AB2+BC2 =202+212=841. D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.  2. 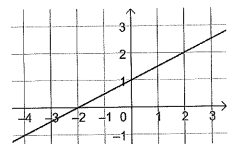On donne la représentation graphique d'une fonction : Fonction affine f(x) = ax +b. f(0) = 1 = b ; f(-2) = 0 soit 0 = -2a+1 ; a =0,5. f(x) = 0,5 x+1.  3. Le carré n°2 est l'image du carré 1 par l'homthétie de rapport -2 et de cente O. 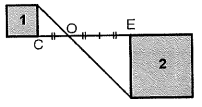  4. Un  cocktail est composé de jus d'ananas, de juus de fruit de la passion et de jus de citron dans le ratio 10 ; 6 ; 2. Pour réaliser 90 cL de ce cocktail, il faut prévoir : 90 x 6 /(10+6+2)= 30 cL de jus de fruit de la passion. 5 Un maraicher a cueilli 408 pommes et 168 poires. Il remplit des sacs comportant le meme nombre de pommes et le même nombre de poires en utilisant tous les fruits. le plus grand nombre de sacs qu'il peut remplir est : 408 = 23x3x17 ; 168 = 23x3x7. PPCM(408 ; 168 )=23 x3 = 24. Il peut remplir 24 sacs contenant 17 pommes et 7 poires. Exercice 2. 17 points. Le graphe suivant compare les coûts prévisionnel et réel pour les JO d'été. 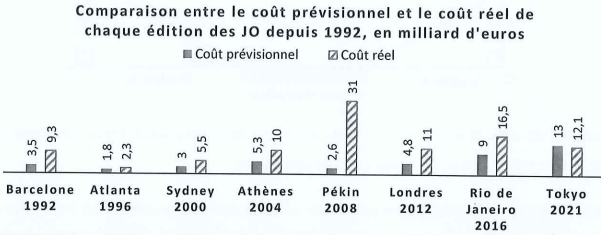 1) Combien d'éditions ont eu un coût réel supérieur ou égal à 10 milliards d'euros ? 5.  2 . Calculer le pourcentage d'augmentation entre le coût prévisionnel et le coût réel lors des JO de Rio en 2016. (16,5 -9) / 9x100 ~83 %.   3.  Montrer que le coût réel moyen est 12,2 milliards d'euros. (9,3 +2,3 +5,5 +10 +31 +11 +16,5 +12,1 ) / 8 =12,2. 4.a. "Cela signifie que la moitié des édditions ont un coût réel supérieur à 12,2 milliards". Cette affirmation est fausse. ( seuls 2 édditions ont un coût réel supérieur à 12,2). Il ne faut pas confondre moyenne et médiane. b. "Le coût prévisionnel moyen des prochains jeux sera de l'ordre de 5,5 milliards d'euros". On appelle x ce coût prévisionnel des prochains jeux ; le coût prévisionnel moyen des 8 jeux précédents est voisin de 5,5 milliards d'euros. (3,5 +1,8+3+5,3+2,6+4,8+9+13 +x) / 9 =5,5. (43 +x) / 9 =5,4. 43+x = 5,5 x9 = 49,5 ; x =6,5. L'affirmation est fausse. Le coût moyen prévisionnel des prochains jeux sera sera sans doute de 5,5 milliards. Exercice 4. 22 points. 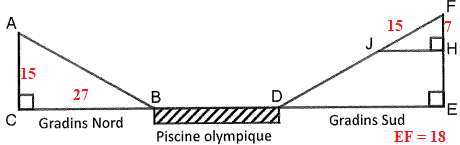1.a Calculer AB. Relation de Pythagore dans le triangle ABC rectangle en C : AB2 = AC2 + BC2 = 152+272= 954 ; AB ~30,9 m ou 31 m.. 1.b. Vérifier que JD ~ 24 m. Dans les triangles FJH et FDE, relation de Thalès : FD / FJ = FE / FH = 18 /7. FD = 18 FJ / 7= 18 x 15 / 7 =38,6 m ; DJ = 38,6 -15 =23,4 ~ 24 m. 2) Le respect des normes de sécurité impose que l'angle ABC soit inférieurà 35°. Le gradin respecte-t-il cette norme ? Dans le triangle rectangle ABC :  tan (ABC) =AC / BC = 15 / 27 =0,555 ; cet angle mesure 29°. La norme est respectée. 3) Le toit du centre a une surface de 5000 m2. 4678,4 m2 sont couverts de panneaux photovoltaïques. ( dimensions d'un panneau : 1,7 m x 1 m) Energie produite par un panneau : 350 kWh par an. Montrer que l'énergie totale produite par an est 963 200 kWh.   Nombre de panneaux : 4678,4 // 1,7 =2752. Energie produite par an : 350 x2752 =963 200 kWh.  4) La température de l'eau de la piscine doit être comprise entre 25 et 28°C. L'eau occupe un pavé droit de dimensions 50 x25 x 3 et sa température doit être de 26°C. Lors de la première mise en chauffe l'eau est à 18°C. Il faut 9,3 kWh pour chauffer 1 m3 d'eau de 18 à 26°C. Quelle quantité d'énergie sera nécessaire pour chauffer l'eau de 18 à 26°C ? Volume d'eau : 50 x25 x3 =3750 m3. Energie : 3750 x 9,3 =34 875 kWh. ... .... Exercice 4 . 18 points. On dispose de deux boîtes contenant des boules numérotées, indiscernables au toucher. La première boîte contient trois boules numérotées 2, 3 et 5. La deuxième boîte contient deux boules numérotées 3 et 5.  On tire au hasard une boule dans la première boîte puis une boule dans la deuxième boîte. On s’intéresse au produit des nombres inscrits sur ces deux boules. Par exemple, si on tire la boule numérotée 2 dans la première boîte puis la boule numérotée 5 dans la deuxième boîte, on obtient comme résultat : 2×5 = 10. 1. Compléter  le tableau à double entrée afin de faire apparaître tous les résultats possibles de cette expérience. 2 3 5 3 6 9 15 5 10 15 25 2. Quelle est la probabilité d’obtenir 15 comme résultat ? 2 cas favorables sur 6 possibles : probabilité d'obtenir 15=2 / 6 = 1 /3.  3. L’affirmation suivante est-elle vraie ? Affirmation : Il y a 2 chances sur 3 d’obtenir un multiple de 3. Cas favorables : 6 ; 9 ;  15 ; 15. 4 cas favorables sur 6 possibilités : probabilité d'obtenir un multiple de 3 =4 /6 = 2 /3. 4. On ajoute une troisième boîte contenant deux boules numérotées avec des nombres entiers. On tire au hasard une boule dans la première boîte, puis une boule dans la deuxième boîte, puis une boule dans la troisième boîte. On multiplie les nombres inscrits sur ces boules et on s’intéresse au produit de ces trois nombres. Anissa a obtenu comme résultat 165 et Bilel a obtenu 78. Quels sont les nombres inscrits sur les boules de la troisième boîte ? Nombre obtenu lors du tirage dans la première boîte : x =2 ; 3 ou 5. Nombre obtenu lors du tirage dans la seconde boîte : y = 3 ou 5. Nombre obtenu lors du troisième tirage u ou v. 6 u = 165 ; u =27,5  n'est pas entier. 9u = 165  ; u = 18,33 n'est pas entier. 10 u =165 ; u = 16,5 n'est pas entier. 15 u = 165 ; u =  11. 25 u = 165 ; u =6,6 n'est pas entier. 6v = 78 ; v =13. 9 v = 78 ; v =8,67 n'est pas entier. 10 v = 78 ; v =7,8 n'est pas entier. 15 v = 78 ; v = 5,2 n'est pas entier. 25 v = 78 ; v =  3,12 n'est pas entier. Exercice 5 . 23 points. Dans cet exercice, les deux parties sont indépendantes. On considère les fonctions f et g définies par f (x) = (x +2)2 − x et g(x) = 7x +4. Partie A 1. Calculer f (−4). f(-4) = (-4+2)2 -(-4)=8. 2. Déterminer un antécédent de 3 par la fonction g. 3 = 7x+4 ; -1 = 7 x ; x = -1 / 7. Partie B Trois élèves, Paul, Jane et Morgane, cherchent à résoudre l’équation f (x) = g(x) par trois méthodes différentes. 1. Paul utilise un tableur. Il calcule ainsi les images des entiers compris entre −3 et 3 par les fonctions f et g. a. Quelle formule a-t-il saisie en cellule B3 puis étirée vers la droite pour compléter la ligne 3 du tableau ? =7*B1+4. b. Avec cette méthode, quelle(s) solution(s) trouve-t-il à l’équation f (x) = g(x) ? x =0. 2. Jane utilise un logiciel de programmation. Le programme qu’elle a créé permet de tester l’égalité f (x) = g(x) pour une valeur de x choisie par l’utilisateur. . Elle décide de tester toutes les valeurs entières entre −5 et 3. a. Compléter  la ligne 4 du programme de Jane afin d’obtenir l’image par la fonction g du nombre choisi.  b. Quelle réponse donne le programme si le nombre choisi est 0 ? Le nombre choisi est solution de l'équation f(x) = g(x).  c. En déduire une solution de l’équation f (x) = g(x). x = 0. 3. Morgane décide de résoudre cette équation par le calcul.  a. Démontrer que l’équation f (x) = g(x) peut se ramener à l’équation x 2 −4x = 0. 7x+4 = (x+2)2 -x= x2+4x+4-x. x2-4x = 0. b. Factoriser l’expression x 2 −4x. x(x-4) = 0. c. En déduire les solutions de l’équation f (x) = g(x). x =0 et x = 4.  4. Dire pour chaque élève s’il a résolu l’équation f (x) = g(x). Expliquer pourquoi. Les deux premiers élèves n'ont trouvé qu'une seule solution. La résolution est incomplète. Le troisième a résolu le problème. .

menu