Mathématiques, DNB Métropole 09 / 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . .. .. ...... ... Exercice 1(20 points) 1. Affirmation 1 La décomposition en produit de facteurs premiers du nombre 260 est 4×5×13 .Faux. 4 nest pas un  nombre premier. 260 = 22 x5x13. 2. Affirmation 2 Une urne opaque contient des boules indiscernables au toucher : 3 boules blanches, 4 boules jaunes et 8 boules rouges. On pioche au hasard une boule dans cette urne et on note sa couleur. Une autre urne opaque contient des boules indiscernables au toucher : 1 boule marquée de la lettre A, 1 boule marquée de la lettre B et 3 boules marquées de la lettre C. On pioche au hasard une boule dans cette urne et on note la lettre obtenue. La probabilité d’obtenir une boule de couleur rouge est supérieure à la probabilité d’obtenir une boule marquée de la lettre C. Faux. Probabilité d'obtenir une boule rouge : 8 possibilités sur 15 ;soit  8 /15. Probabilité d'obtenir la lettre C : 3 possibilités sur 5 soit 3 /5 = 9 /15. 3. Affirmation 3. La solution de l'équation 7x+5=2x−2 est −1,4. Vrai. 7x-2x=-2-5 ; 5x=-7 ; x=-7 /5= -1,4. 4. Affirmation 4. On empile 10 pièces cylindriques de 1,9 cm de diamètre et de 0,2 cm de hauteur. Le volume du cylindre, arrondi à l’unité, formé par les 10 pièces est de 6 cm3. Vrai. Hauteur h = 0,2 x10 = 2 cm. Rayon R = 0,95 cm. Volume p R2 h =3,14 x 0,952 x2 =5,67 ~ 6 cm3. 5. Affirmation 5 Un éléphant qui court à une vitesse de 5 m/s est plus rapide qu’un cochon qui se déplace à une vitesse de 17 km/h. Vrai. 17 / 3,6 = 4,72 m /s.   Exercice 2  20 points. Un agriculteur possède un champ de blé ayant la forme d'un triangle ABC rectangle en B représenté ci-dessous. On donne AB = 200 m et BC = 150 m. 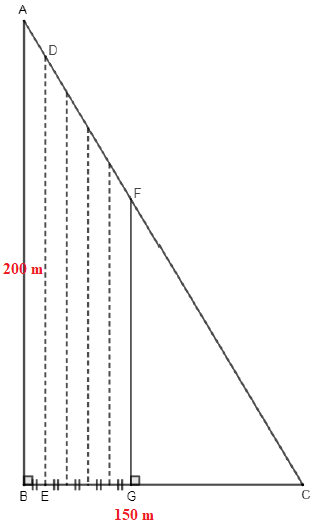Pour moissonner son champ, il utilise une moissonneuse batteuse qui, à chaque passage, coupe des bandes de 12 mètres de large parallèles à la droite (AB). On a donc BE = 12 m. Il commence à passer le long du côté [AB]. Le segment en pointillés [DE] représente la limite du premier passage de la moissonneuse batteuse. Après avoir fait 5 passages, il a moissonné le quadrilatère ABGF. 1. a. Montrer que BG = 60 m. BG = 5x12 = 60 m. b. En déduire que CG = 90 m. CG =BC-BG = 150-60 = 90 m. 2. Démontrer que la longueur GF est de 120 m. Relation de Thalès : GF / AB = GC / BC ; GF = AB x GC / BC = 200 x90 / 150 =120 m. 3. a. Démontrer que l’aire du triangle rectangle CGF est de 5 400 m2. CG x GF / 2 =90 x 120 / 2 =5 400 m2. b. Le quadrilatère ABGF a une surface de 9 600 m2 qui a été moissonnée en 80 minutes. On admet que le temps de travail de la moissonneuse batteuse est proportionnel à la surface moissonnée. Calculer le temps de travail qu’il faut pour moissonner la partie restante CGF de son champ. Surface restante à moissonner : 5 400 m2. Surface moissonnée / durée = 9600 / 80 =120 m2 / min. 5 400 / 120 =45 min. 4. L'année suivante, il décide de clôturer son champ ABC afin d'y mettre des animaux pour l'été. Quelle longueur de clôture doit-il acheter ? Relation de Phytagore dans le triangle ABC rectangle en B : AC2 = AB2 + BC2 =2002+1502=62 500 ; AC =250 m AB +BC +AC = 200 +150 +250 =600 m. Exercice 3. 20 points. Une entreprise décide de faire poser sur le toit de son hangar des panneaux solaires. Pendant une semaine d'utilisation, les productions d’électricité journalières en kilowattheures (kWh) de ces panneaux ont été relevées dans le tableau ci-dessous. jour lundi mardi mercredi jeudi vendredi samedi dimanche Production ( kWh) 381 363 322 329 393 402 376 1. a. Quel jour la production d’électricité a-t-elle été la plus grande ? Samedi : 402 kWh. b. Calculer l'étendue de ces productions d’électricité. 402-322=80 kWh. c. Quelle est la production moyenne d’électricité par jour sur cette période ? (381+363+322+329+393+402+376)/7=2566 / 7~367 kWh. 2. L’entreprise revend 15 % de sa production d’électricité au tarif de 8 centimes le kWh. Combien a-t-elle gagné en euros pendant ces 7 jours ? 2566 x0,15 x8=3079 centimes = 30,79 €. 3. Afin que les panneaux solaires aient une production maximale, le toit doit avoir une pente avec l’horizontale comprise entre 30°et 35°. 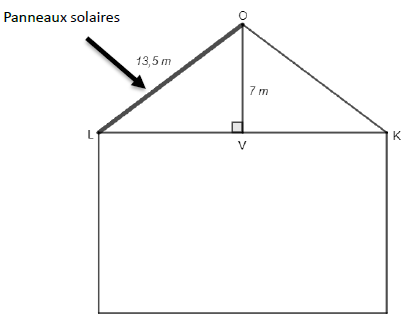Sur ce toit, les panneaux solaires ont-ils une production maximale ? Sinus de l'angle OLV = OV / OL = 7 / 13,5 =0,519. Cet angle mesure environ 31°. La production est maximale. ... .... Exercice 4. 20 points On considère la fonctionf définie par f(x)=x2+10x+16. 1. Vérifier par le calcul que l'image de 6 par la fonction f est 112. f(6) = 62 +10 *6 +16=112. 2. On utilise un tableur afin de calculer les images des entiers compris entre −4 et 4 par la fonction 𝑓f. A B C D E F G H I J 1 x -4 -3 -2 -1 0 1 2 3 4 2 f(x) -8 -5 0 7 16 27 40 55 72 a. Parmi les 4 formules ci-dessous, recopier celle qui a été saisie dans la cellule B2, puis étirée vers la droite afin de calculer les images des nombres donnés par la fonction f. =B1*B1+10*B1+16 Vrai. =A1*A1+10*A1+16 =(-4)*(-4)+10*(-4)+16 =𝑥∗𝑥+10∗𝑥+16 b. En utilisant le tableau, déterminer un antécédent de 0. f(-2) = 0. 3. a. Démontrer que f(x)peut s’écrire (x+2)(x+8). (x+2)(x+8) = x2 +8x+2x+16 = x2 +10x+16 = f(x). b. En déduire un autre antécédent de 0 par la fonction f. f(-8)=0. Exercice 5 (20 points) La quadrilatère ABCD ci-dessous est constitué de 2 triangles équilatéraux de côté 5 cm. 1. a. Reproduire le quadrilatère ABCD en vraie grandeur. b. Quelle est sa nature ? Losange : 4 côtés égaux. c. Démontrer que l’angle BCD mesure 120°. Dans le triangle équilatéral ACD, l'angle ACD mesure 60°. Dans le triangle équilatéral ABC, l'angle ACB mesure 60°. L'angle BCD est la somme des deux angles ACB et ACD ; il mesure donc 60 +60 = 120°. 2. Le programme ci-dessous permet de créer le bloc Motif qui trace le quadrilatère ABCD. Recopier et compléter les lignes 5 et 6 de ce programme. On utilise l’échelle suivante :10 pas dans le programme représentent 1 cm dans la réalité. 3. Recopier et compléter les trois phrases suivantes afin d’associer chaque figure au programme qui permet de la tracer.

menu