Exercice 1 (20 points)
1.
Anne et Jean ont acheté 630 dragées roses et 810 dragées blanches
qu'ils ont mises dans un sachet. On suppose que les dragées sont
indiscernables au toucher.
a. Combien Anne et Jean ont-ils acheté de dragées au total ?
810+630=1440.
b. Anne prend au hasard une dragée dans le sachet. Quelle est la probabilité qu'elle obtienne une dragée blanche ?
810 / 1440=81 / 144 = 9 / 16=0,5625.
2. Avec ces dragées, ils réalisent des ballotins pour leur mariage de sorte que :
- le nombre de dragées roses est le même dans chaque ballotin ;
- le nombre de dragées blanches est le même dans chaque
- toutes les dragées soient utilisées.
a. Peuvent-ils réaliser 21 ballotins ?
630 / 21=30 ; 810 / 21diffère d'un nombre entier.
Ils ne peuvent pas réaliser 21 ballotins.
b. Décomposer 630 et 810 en produits de facteurs premiers.
630 =2 x3
2 x 5 x 7.
810 = 2 x 3
4 x 5.
c. En déduire le nombre maximum de ballotins qu'Anne et Jean pourront réaliser.
Donner alors la composition de chaque ballotin.
PGCD(630 et 810) =2 x3
2 x5 =90.
630 / 90= 7 dragées roses et 810 / 90 = 9 dragées blanches.
Exercice 2. QCM. 18 points.
Question 1 . Quelle est l'écriture scientifique de 13 420 ?
1,342 10
4. Réponse
B.
Question 2. On a relevé, en mètres, les onze meilleures performances du lancer de marteau chez les
hommes: 85,14; 85,14; 85,20 ; 85,60 : 85,68 ;
85,74 ; 86,04 ; 86,34 ; 86,51 ; 86,66 ; 86,74.
Quelle est la médiane de cette série ?
85,74. Réponse
A.
Question 3.
Quelle est l'image du motif gris par la symétrie d'axe (d) ?
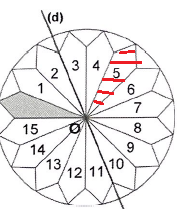
Motif 5. Réponse
C.
Question 4. Quelle est l'image du motif gris par la rotation de centre O et
d'angle 90° dans le sens antihoraire ?
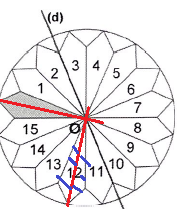
Motif 12. Réponse
B.
Question 5. Quelle est l'image de 2 par la fonction f ?
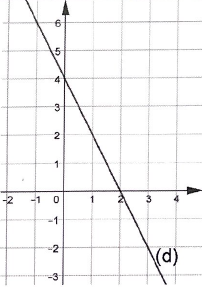
f(2) = 0. Réponse
A.
Question 6. Quel est le coefficient directeur de la droite (d) ?
-4 / 2 = -2.
Réponse C.
Exercice 3. (22 points).
Exercice 3 (22 points)
Sur la figure ci-après, qui n'est pas à l'échelle, on a représenté le trajet de la course que doit faire Oscar.
Dans le triangle DLA rectangle en L, le point J appartient au segment [DA] et le point K appartient au segment [DL].
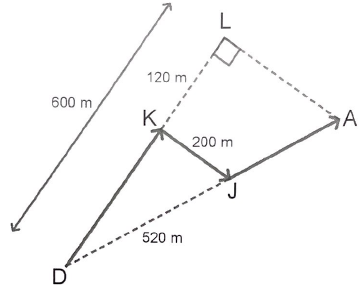
1. Montrer que la longueur DK est égale à 480 m.
DK = DL -KL = 600-120 =480.
2. Montrer que le triangle DKJ est rectangle en K.
Relation de Pythagore dans le triangle DKJ rectangle en K :
DK2 = 4802=230 400. KJ2 = 2002=40 000.
DK2 +KJ2 =270 400.
DJ2 =5202=270 400.
DK2 +KJ2 =
DK2 .
D'après la récioroque du théorème de Pythagore, le triangle DKJ est rectangle en K.
3. Justifier que les droites (KJ) et (LA) sont parallèles.
Les droites (LA) et (KJ) sont perpendiculaires à la droite (DL). Les droites (KJ) et (LA) sont donc parallèles.
4. Montrer que le segment [DA] mesure 650 m.
Relation de Thalès : DL / DK = DA / DJ ; DA = DL * DJ / DK = 600 * 520 / 480 =650 m.
5. Calculer la longueur du trajet DKJA, fléché sur la figure.
DK +KJ +JA = 480 +200 +(650-520)=810 m.
6. Un photographe
place une caméra au point D. Afin de filmer l'ensemble de la course
sans bouger la caméra, l'angle LDA doit être inférieur à 25°. Est-ce le
cas ?
Tangente de cet angle = KJ / DK = 200 / 480 =0,417.
Cet angle mesure environ 22,6 °.