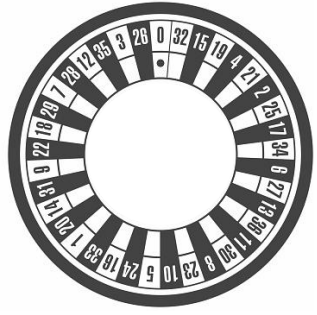
Mathématiques, DNB Métropole 2024 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1 (20 points)  Au casino, la roulette est un jeu de hasard pour lequel chaque joueur mise au choix sur un ou plusieurs numéros. On lance une bille sur une roue qui tourne, numérotée de 0 à 36. La bille a la même probabilité de s’arrêter sur chaque numéro. 1. Expliquer pourquoi la probabilité que la bille s’arrête sur le numéro 7 est 1/ 37 . Un seul cas favorable ( arrêt sur le 7 ) ; 37 cas possibles. Probabilité d'arrêt sur le chiffre 7 : 1 / 37.  2. Déterminer la probabilité que la bille s’arrête sur une case à la fois noire et paire. 10 cases sont noires et paires :(2 ; 4 ; 6 ; 8 ; 10 ; 20 ; 22 ; 24 ; 26 et 28). Probabilité d'un arrêt sur une case noire et paire : 10 / 37.  3. a. Déterminer la probabilité que la bille s’arrête sur un numéro inférieur ou égal à 6. 7 cases (0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6). Probabilité d'arrêt sur un numéro inférieur ou égal à 6 : 7 / 37.  b. En déduire la probabilité que la bille s’arrête sur un numéro supérieur ou égal à 7. 1-7 / 37 = (37-7) / 37 = 30 / 37~0,81. c. Un joueur affirme qu’on a plus de 3 chances sur 4 d’obtenir un numéro supérieur ou égal à 7. A-t-il raison ? 3 / 4 = 0,75  ;  0,81 > 0,75, il a raison. Exercice 2. 20 points. 1. a. Vérifier que, si on choisit 5 comme nombre de départ, le résultat du programme A est 56. 52 x2+2x5-4 =56.  b. Quel résultat obtient-on avec le programme B si on choisit −9 comme nombre de départ ? -9+2 =-7 ; -9-1 = -10 ; -7 x(-10) = 70. 2. On choisit un nombre quelconque x comme nombre de départ.  a. Parmi les trois propositions ci-dessous, recopier l’expression qui donne le résultat obtenu par le programme B ?  (x + 2) − 1  ; (x + 2) × (x − 1) exact ;   𝑥 + 2 × 𝑥 − 1 . b. Exprimer en fonction de x le résultat obtenu avec le programme A. 2x2 +2x-4.  3. Démontrer que, quel que soit le nombre choisi au départ, le résultat du programme A est toujours le double du résultat du programme B. Programme B : (x+2)(x-1) = x2+2x-x-2 =x2+x-2. Programme A : 2(x2+x-2). Exercice3. 22 points. Sur la figure ci-dessous, on a :  C est un cercle de centre O et de rayon 4,5 cm ;   [AB] est un diamètre de ce cercle et D est un point du cercle ;  les points B, E, A sont alignés, ainsi que les points D, F, A ;  les droites (BD) et (EF) sont parallèles ;  BD = 5,4 cm ; DA = 7,2 cm et AE = 2,7 cm. 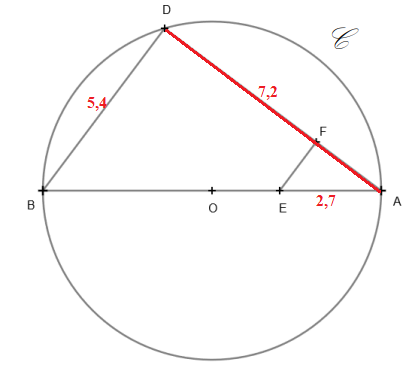1. Justifier que le diamètre [AB] mesure 9 cm. AB est le diamètre du cercle de rayon 4,5 cm. AB = 2 x4,5 = 9 cm. 2. Démontrer que le triangle ABD est rectangle en D. : AB2 =81 ;  BD2+AD2 =5,42 +7,22 =81. D'après la réciproque du théorème de Pythagore, le triangle ABD est rectangle en D. 3. Calculer AF. Dans les triangles ABD et AEF :  les droites (BD) et (EF) sont parallèles ; d'après le théorème de Thalès : BD / EF = AD / AF =AB / AE = 9 /2,7 . AF = 2,7 AD / 9 = 2,7 x7,2 / 9 =2,16 cm. 4. a. Justifier que l’aire du triangle ABD est égale à 19,44 cm2. AD x BD / 2 = 5,4 x7,2 / 2 =19,44 cm2.  b. Calculer l’aire du disque, arrondie au centième. p R2 =3,14 x4,52 ~ 63,62 cm2.  5. Quel pourcentage de l’aire du disque représente l’aire du triangle ABD ? 19,44 / 63,62 x100 =30,56 %. ... .... Exercice 4  QCM. 18 points 1. On considère la fonction f définie par f(x) =3x – 2. Quelle est l’image de – 4 par cette fonction ? f(-4) = 3*(-4) -2 = -14. Réponse A. 2. Combien vaut (-5)3 ? -5 *(-5) *(-5)= -125. Réponse A. 3.   Quelle est l’image du point J par la translation qui transforme C en A ? Réponse B. 4. Quel est l’antécédent de 3 par la fonction f ? Réponse C. 45. On a mesuré les tailles, en m, de sept élèves : 1,46 ; 1,65 ; 1,6 ; 1,72 ; 1,7 ; 1,67 ; 1,75 Quelle est la médiane, en m, de ces tailles ? 1,46 ; 1,6 ; 1,65 ; 1,67 ; 1,7 ; 1,72 ; 1,75. Réponse B. 6. Dans le triangle ABC rectangle en A , qui n’est pas en vraie grandeur, quelle est la valeur de cos a ? cos a = AB / BC = 4 / 5 = 0,8. Réponse A. Exercice5 . 20 points. Un club de natation propose un après-midi découverte pour les enfants.  PARTIE A  La présidente du club veut offrir des petits sachets cadeaux tous identiques contenant des autocollants et des drapeaux avec le logo du club. Elle a acheté 330 autocollants et 132 drapeaux et veut tous les utiliser. Elle veut que, dans chaque sachet, il y ait exactement le même nombre d’autocollants et que, dans chaque sachet, il y ait exactement le même nombre de drapeaux. 1. Pourquoi n’est-il pas possible de faire 15 sachets ? 132 / 15 = 8,8 ; 15 n'est pas un diviseur de 132. 2. a. Décomposer 330 et 132 en produits de facteurs premiers. 330 = 2 x3 x5 x11. 132 = 22 x 3 x11.  b. En déduire le plus grand nombre de sachets que la présidente pourra réaliser. PPCM(330 et132 = 2 x3 x11 = 66.  c. Dans ce cas, combien mettra-t-elle d’autocollants et de drapeaux dans chaque sachet ? 330 / 66 =5 autocollants et 132 / 66 = 2 drapeaux. PARTIE B La piscine a la forme d’un pavé droit (largeur 15 m, longueur 25 m, hauteur 2 m).. Elle est remplie aux 9 /10 du volume. 1 m3 d’eau coûte 4,14 €. Combien coûte le remplissage de la piscine ? Volume d'eau : 15 x25 x2 x0,9 =675 m3. 675 x4,14 =2794,5 €. .

menu