Physique chimie .
Partie A - Les coraux (5 points)
Pour se développer de manière optimum, les coraux doivent se trouver
dans des eaux de mer dont le pH est compris entre 8,0 et 8,4.
1. Préciser si les eaux de mers favorables aux coraux sont des solutions acides ou des solutions basiques. Justifier.
A 25°C, à pH surrieur à 7, la solution est basique.
Les coraux sont des êtres vivants marins dont le squelette est constitué de carbonate de calcium de formule chimique CaCO
3.
2. Indiquer le nombre d’atomes de carbone (C) et
le nombre d’atomes d’oxygène (O) figurant dans la formule chimique du
carbonate de calcium.
Un atome de carbone et trois atomes d'oxygène.
Partie B – L’environnement marin des coraux (9 points)
Le squelette des coraux contient des ions calcium Ca
2+ provenant de l’eau de mer.
Afin de vérifier la présence de l’ion calcium Ca
2+ dans une eau de mer, on souhaite réaliser un test caractéristique sur un échantillon d’eau de mer.
3. Proposer un protocole expérimental permettant de vérifier la présence de l’ion calcium Ca
2+ dans l’eau de mer testée.
4. Dans l’expérience de la question 3, iIndiquer l’observation attendue à l’issue du test si l’eau de mer contient des ions Ca
2+.
Verser 10 mL d'eau de mer dans un becher. A l'aide d'un compte gouttes
ajouter quelques gouttes d'oxalate d'ammonium. On observe la formation
d'un précipité blanc d'oxalate de calcium en présence d'ion calcium.
Pour déterminer la masse volumique d’une eau de mer, on réalise les mesures suivantes :
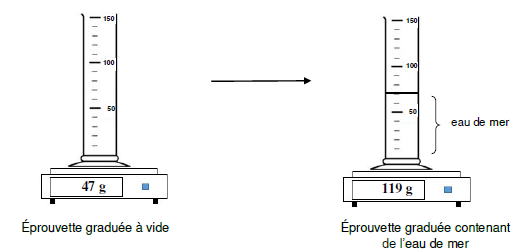
Volume d'eau de mer : 70 mL ; masse de cette eau : 119-47 =72 g.
Masse volumique = masse / volume = 72 /70 ~1,03 g/ mL.
Partie C – Descente d’un plongeur (6 points)
Lors d’une plongée, un plongeur est soumis à deux forces :
- son poids P qui modélise l’action exercée par la Terre ;
- la « poussée d’Archimède » F qui modélise l’action exercée par l’eau.
Ces deux forces sont représentées par des segments fléchés A et B.
 6.
6. Indiquer lequel des deux segments fléchés A et B correspond au poids P du plongeur. Justifier.
Le poids est une force verticale dirigée vers le bas : donc B.
Pour qu’un plongeur puisse descendre, il faut que la valeur de son poids soit supérieure à la valeur de la poussée d’Archimède.
Un plongeur a une masse m = 90 kg.
7. Calculer la valeur du poids P de ce plongeur.
Donnée : intensité de la pesanteur sur Terre g = 10 N/kg.
P = m g = 90 x10 = 900 N.
La valeur de la poussée d’Archimède exercée sur ce plongeur a pour valeur F = 850 N.
8. En déduire si le plongeur va pouvoir descendre. Justifier.
Le poids étant supérieur à la poussée, le plongeur descend.
Partie D - Profondeur de plongée (5 points)
La profondeur d’un fond marin peut être déterminée à l’aide d’un sonar placé sous la coque d’un bateau .
Le sonar émet un signal sonore qui se réfléchit sur le fond marin à la
profondeur d. La mesure de la durée d’un aller-retour du signal
sonore permet de déterminer la profondeur d sachant que la vitesse de
propagation d’un signal sonore dans l’eau de mer est v = 1500 m/s.
La profondeur d’un fond marin a été déterminée par un bateau équipé d’un sonar à partir de la durée T d’un
aller-retour du signal sonore. La valeur mesurée est T = 0,04 s.
9. Déterminer la profondeur d à laquelle se trouve le fond marin. Expliquer la démarche.
Distance aller + distance retour = v T.
2d = v T ; d = v T / 2 =1500 x0,04 / 2= 30 m.