Exercice 1. 20 points
Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n’est demandée.
Pour chaque question, quatre réponses sont proposées, une seule réponse est exacte.
1. Donner l’écriture scientifique de 0,193 × 10
−100
.
1,93 x10
-1 x10
-100 = 1,93 × 10
-101.
2. Lili part en vacances, elle parcourt 480 km en 5 h 42 min.
Quelle est sa vitesse moyenne en km/h, arrondie au dixième ?
42 min = 42 /60 heure =0,7 heure.
480 / 5,7 =84,2 km / h.
3. Sam fait tourner la roue ci-dessous et regarde le nombre désigné
par la flèche, qui peut être 1 ou 2.
On admet que chaque secteur a autant de chance d’être
désigné.
Le nombre écrit dans un des secteurs a été effacé. Est-il possible
d’écrire un nombre dans ce secteur de sorte que la probabilité
que la flèche désigne le nombre 2 soit égale à 3
/5
?
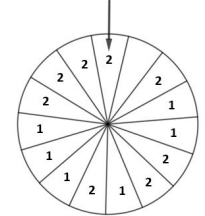
15 secteurs ;probabilité du nombre 2 = nombre de cas favorables / 15 = 3 /5.
Nombre de cas favorables = 3 / 5 x15 =9.
Il faut écrire le nombre 2 dans le secteur effacé.
4. On considère la liste de nombres suivante : 5 ; 1 ; 3 ; 10 ; 17 ; 11 ; 10. Pour cette liste de
nombres, que représente le nombre 5 ?
Suite ordonnée : 1 ; 3 ; 5 ; 10 ; 10 ; 11 ; 17. La médiane est 10.
Moyenne :(1+3+5+10+10+11+17) / 7 =57 / 7.
Etendue : 17-1 = 16.
5 ne représente donc rien de particulier.
5. Léa achète un vélo électrique. Pour le réserver, elle paye 1/
5
du prix au magasin. Le magasin lui
propose de payer le reste en trois paiements d’un même montant. Quelle fraction du prix du
vélo représente l’un de ces trois paiements ?
On note x le prix du vélo. il reste à payer 0,8 x en trois fois.
Chaque fraction du prix correspond à 0,8 /3 =8 /30 =4 /15.
Exercice 2 (20 points).
Un entraîneur de sport prépare deux circuits d’entraînement contenant plusieurs exercices de
cardio et de renforcement musculaire :
• un circuit commence à l’exercice 1 et se termine en revenant à l’exercice 1 ;
• le circuit 1 contient cinq exercices.
Chaque exercice dure 40 secondes et doit être suivi de
16 secondes de repos permettant de se rendre à l’exercice suivant ;
• le circuit 2 contient dix exercices. Chaque exercice dure 30 secondes et doit être suivi de 5
secondes de repos permettant de se rendre à l’exercice suivant.
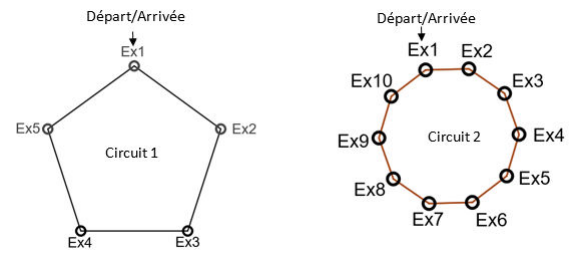1. Montrer que le circuit 1 s’effectue en 280 secondes et que le circuit 2 s’effectue en 350
secondes.
Circuit 1 : 5 x(40+16) =280 s.
Circuit 2 : 10x(30+5) = 350 s.
2. Donner la décomposition en produit de facteurs premiers de 280 et de 350.
280 = 2
3 x5 x7 ; 350 =2 x5
2x7.
3. Une séance d’entraînement est constituée de plusieurs tours du même circuit.
Au coup de sifflet de l’entraîneur, Camille commence une séance d’entraînement sur le circuit 1
et Dominique sur le circuit 2.
a. Expliquer pourquoi, lorsque 2 800 secondes se sont écoulées à partir du coup de sifflet,
Camille se trouve de nouveau au départ du circuit 1.
Préciser où se trouve Dominique sur le circuit 2 lorsque 2 800 secondes se sont écoulées.
Camille a effectué 10 fois le circuit 1 et se retrouve au départ de ce circuit.
Dominique a effectué 8 fois le circuit 2 et se retrouve au point de départ.
b. Après le coup de sifflet, combien de temps faut-il à Camille et Dominique pour se retrouver
en même temps pour la première fois au départ de leur circuit ? Exprimer cette durée en
minute et seconde.
On cherche le plus petit multiple commun à 280 et 350.
2
3 x5
2 x7 =1400 s ou 23 min 20 s.
Exercice 3 (20 points).
On considère le programme de calcul suivant :
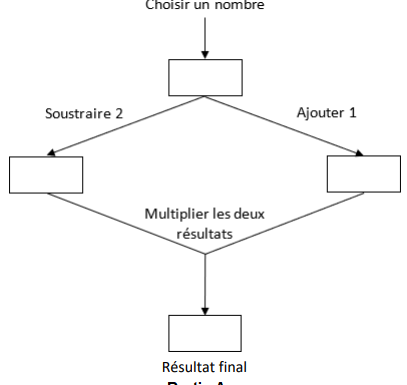Partie A
1. Justifier qu’en choisissant 5 comme nombre de départ, le résultat final obtenu est 18.
5-2 = 3 ; 5+1 = 6 ; 3 x6 = 18.
2. Calculer le résultat final donné par ce programme lorsque le nombre de départ choisi est −
3 /2
-1,5-2 = -3,5 = -7 /2 ; -1,5 +1 = -0,5 = -1/2 ; -7/2 x(-1 /2) = 7 /4.
.
3. Le script suivant, écrit avec un logiciel de programmation, correspond au
programme de calcul ci-dessus.
Compléter les lignes 3, 4 et 5 du script.
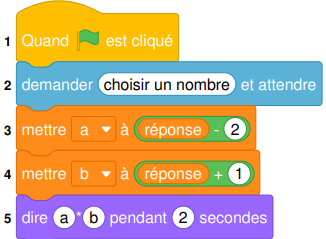Partie B
Soit la fonction g définie, pour un nombre x donné, par g(x) = 𝑥
2 − 𝑥 − 2.
1. Prouver que (𝑥 − 2)(𝑥 + 1) = 𝑥
2 − 𝑥 − 2.
(x-2)(x+1) = x
2+x-2x-2 =
𝑥2 − 𝑥 − 2.
2. a. Résoudre l’équation (𝑥 − 2)(𝑥 + 1) = 0.
x-2 =0 ; x = 2.
x+1=0 ; x = -1.
b. En déduire les antécédents de 0 par la fonction g.
Les antécédents de zéro par la fonction g sont -1 et 2.
