Exercice 4 . 26 points.
Des amis habitent Strasbourg et préparent leurs vacances. Cette année ils ont décidé de
partir découvrir une grande ville française pendant une semaine. Pour s’y rendre, ils louent
une voiture. Une fois arrivés sur place, ils feront ensuite tous leurs trajets à pied ou en
transport en commun.
Une agence de location de voitures propose les trois formules suivantes pour une location
sur 1 semaine :
A. 0,50 € par km parcouru ; B. forfait 300 € +0,25€ par km ; C : forfait 900 € kilométrage illimité.
PARTIE A : Les amis souhaitent se rendre à Marseille. (803 km).
Ils ont un budget de 1 000 € pour le
voyage.
1) Quelle distance, en km, vont-ils parcourir pour le trajet aller-retour ?
2 x803 = 1606 km.
2) En choisissant la formule B, montrer que la location de voiture coûtera 701,50 €.
300+0,25 x1606 =701,5 €.
3) Quelle est la formule la plus avantageuse ?
Avec la formule A : 0,50 x1606 =803 €.
La formule B est la plus avantageuse.
4) Voici des informations pour le voyage :
- prix moyen du gazole : 1,87 € le litre.
- consommation : 5,6 L aux 100 km.
- péage : 115,80 €.
Leur budget sera t-il suffisant ?
Consommation :1606 / 100 x5,6 =89,94 litres.
Coût du carburant : 89,94 x1,87 =168,18 .€.
Total dépenses avec la formule la plus avantageuse : 701,5 +115,8 +168,18 =985,48 €.
Le budget est suffisant.
5) Soit 𝑥 le nombre de kilomètres parcourus, exprimer en fonction de 𝑥 le prix payé pour
chaque formule de location.
A : 0,5 x ; B : 300 +0,25 x ; C : 900.
6) On a représenté ci-dessous, pour chacune des formules, le coût de la location (en euros)
en fonction de la distance parcourue (en kilomètres).
Associer chaque courbe à la formule de location correspondante. Ne pas justifier.
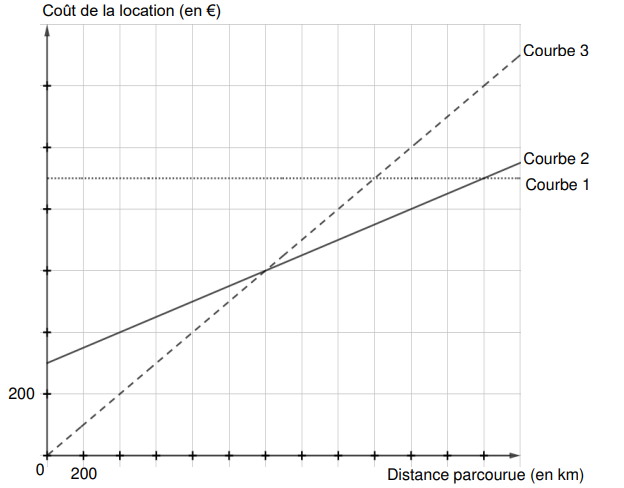
Courbe 1 : formule C.
Courbe 3 : formule A.
Courbe 2 : formule B.
7) Résoudre l’équation 0,25𝑥 + 300 = 0,5𝑥. Interpréter ce résultat.
300 = 0,25 x ; x = 300 / 0,25 =1200.
En parcourant1200 km les formules A et B conduisent à la même dépenses de location.
8) a. Si la distance parcourue est de 2 500 km, quelle formule doit-on choisir pour payer le
moins cher ? Ne pas justifier.
Formule C.
b. Donner une distance parcourue pour laquelle la formule A est la plus intéressante. Ne
pas justifier.
Distance inférieure à 1200 km.
c. Déterminer graphiquement quelle formule de location est la moins chère en fonction de
la distance parcourue pour une distance inférieure à 2 600 km.
Moins de 1200 km : formule A.
1200 km : formule A ou B.
De 1200 km à 2400 km : formule B.
De 2400 à 2600 km : formule C.
Exercice 5 . 16 points.
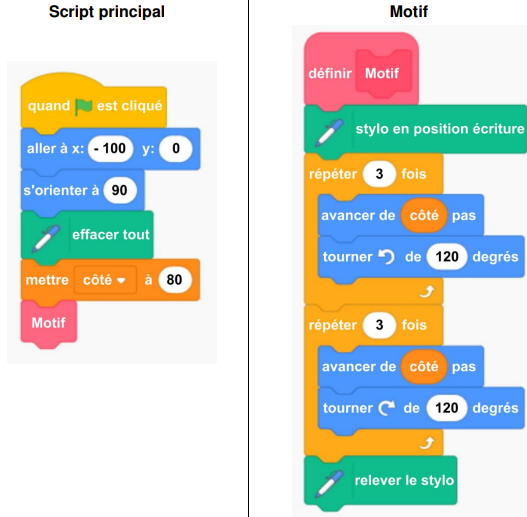 1)
1) À quelles coordonnées le lutin se positionne-t-il juste après avoir cliqué sur le drapeau vert ?
-100 ; 0.
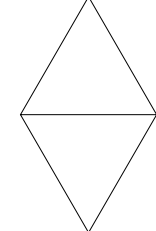
2) En prenant 1 cm pour 20 pas, dessiner en vraie grandeur la figure obtenue en exécutant le
script principal.
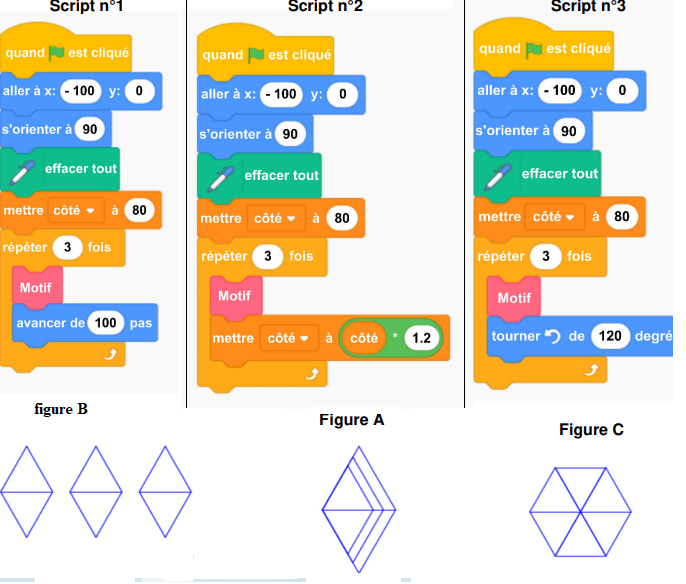
 3)
3) On modifie le script principal de trois façons différentes. Associer chaque script à la figure
qui lui correspond.
 4)
4) Dans cette question on s’intéresse au script n° 2.
a. Combien de fois le bloc « motif » est-il exécuté ?
Trois fois.
b. Quelle est la valeur de la variable « côté » à la fin de ce script ?
La variable coté a été multipliée trois fois par 1,2 : 80 x1,2
3 = 138,24.
.