Points
de règlement au tennis de table,
bac Amérique du
nord 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
. |
..
..
......
...
|
Le serveur lance alors la balle verticalement vers le haut, seulement avec la main, et sans lui communiquer d'effet, de
telle maniere qu'elle s'élève d'au moins 16 cm apreès avoir quitté la
paume de la main libre et retombe ensuite sans toucher quoi que ce soit
avant d'être frappée.
La surface de jeu peut être faite de n'importe quelle matière et
doit permettre un rebond uniforme d'environ 23 cm lorsqu'on
laisse tomber une balle réglementaire sur cette surface d'une hauteur de 30 cm au-dessus d'elle.
Dans tout l'exercice la balle est modélisée par un objet ponctuel dont
on étudie le mouvement assimile a celui de son centre de masse, note M.
Dans les conditions de !'expérience, le champ de pesanteur terrestre
local est supposé uniforme et les frottements liés a l'action de
l'air sont négligés.
Le mouvement du point M est etudie dans le referentiel terrestre
suppose galiléen et muni d'un repere d'axes (Ox, Oy), respectivement
horizontal muni du vecteur unitaire i et vertical muni du vecteur
unitaire j orienté vers le haut.
1. Trajectoire d'une balle lors du lancer
La vidéo d'un joueur au service en compétition permet d'obtenir la
chronophotographie suivante. On peut alors, à l'aide d'un logiciel
d'analyse, tracer l'évolution de la valeur de la vitesse de la balle en
fonction du temps.
A la date t = 0 ms, la balle quitte la main du joueur : son centre de
masse note M se trouve alors a l'origine du repère O et son vecteur
vitesse initiale est note v0, verticale vers le haut.
Q.1. Exprimer les composantes ax et ay du vecteur acceleration a du point M, a un instant quelconque du mouvement.
La balle lancer verticalement n'est soumise qu'à son poids:
ax =0 ; ay = -g.
Q.2. Justifier a
l'aide de la figure que la norme du vecteur vitesse de la balle v(t)
est assimilable à la valeur de sa composante verticale Vy. On notera
pour la suite de l'exercice Vy(t) = v(t).
Q.3. En deduire
qu'a un instant quelconque du mouvement !'expression littérale de la
vitesse v(t) du point M peut être modélisée sous la forme : v( t) = - g
x t + v0
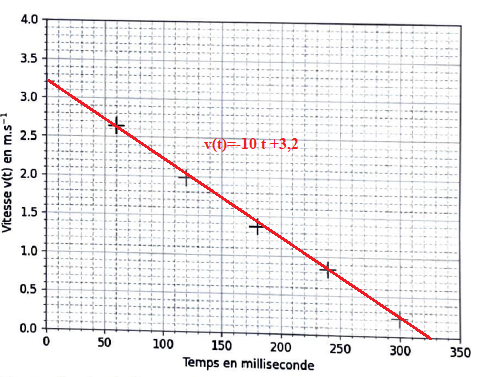
V(t) = -10 t +3,2= - gt + V0.
Q.4. Justifier sans calcul que ce modèle de la vitesse v(t) est en accord avec les points expérimentaux.
Les points expérimentaux sont alignés. La droite passant par ces points a pour équation : v(t) = -10 t +3,2.
Q.5. En déduire une valeur de l'intensite du champ de pesanteur terrestre local, g.
g = 10 m s-2.
Q.6. Proposer une
origine a l'écart observé avec la valeur de référence de l'intensité du
champ de pesanteur terrestre local, g = 9,81 N·kg-1.
Les frottements sur l'air ne sont pas négligeables.
Q. 7. Montrer que !'expression littérale de l!'équation horaire de la position du point M au cours de son mouvement s'écrit :
y(t) =-½gt2 +v0t.
La position est une primitive de la vitesse et la position initiale est l'origine du repère.
y(t) =-½gt2 +v0t.
On note hmax la hauteur maximale atteinte par le centre de masse M de la balle lors du lancer.
On dispose d'un programme ecrit en langage python, python 1 qui, après saisie de hmax donne accès à la valeur de v0.
Q.8. Exploiter les expressions de y(t) et v(t), pour justifier la formule v_o = np.sqrt(2*g*h_max) présente à la ligne 6.
Au point le plus haut, la vitesse est nulle : - gt + v0=0 ; t = v0 / g.
Repport dans y(t) : hmax= -½g(v0 / g)2+v0 2/ g. = -½v02 /g+v0 2/ g = ½v0 2/ g.
v0 = (2ghmax)½.
Q.9. Recopier et compléter cette fenètre d'exécution en deéterminant la valeur de hmax lorsqu'on se place dans la condition décrite aà !'article 2.6.2 du réglement de la F.F.T.T.
hmax > 0,16
Q.10. Calculer alors la valeur minimale de v0 que le programme va afficher.
v0 = (2ghmax)½= (2 x9,81 x0,16)½ =1,77 ~1,8 m /s.
On souhaite faire évoluer le programme précédent pour afficher la vitesse de lancer en km·h-1.
Q.11. Compléter sur votre copie la ligne 8 du programme afin de calculer la vitesse de lancer en km·h-1 .
vinitiale= 3,6 v0.
2. Qualité d'une balle de tennis de table
Pour vérifier la qualitée d'une balle de tennis de table, .un élève
réalise une vidéo de la chute et du rebond d'une balle lachée sans
vitesse initiale depuis une hauteur h = 30 cm. Le pointage des
positions de l'objet lors des différentes phases de son mouvement lui
permet d'effectuer son étude énergétique.
Q.12. Associer, pour la premiere phase du mouvement (temps compris entre 0,00 et 0,24 s), les
symboles aux énergies mécanique, cinétique et potentielle de pesanteur en justifiant les choix.
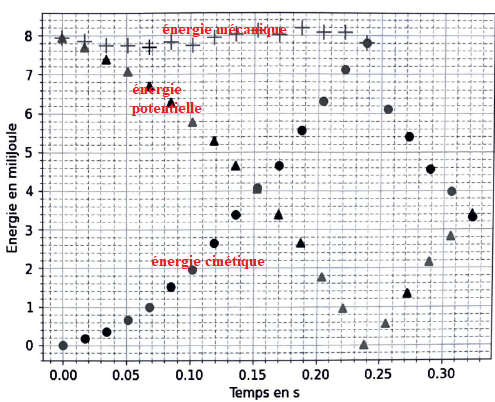
L'énergie mécanique est constante ( frottements négligés).
L'énergie potentielle de pesanteur diminue lors de la chute et l'énergie cinétique augmente.
On réalise une étude énergétique dans la phase après le rebond (à partir de t > 0,24 s).
Q.13. Vérifier par
le calcul, à l'aide de quelques données expérimentales prises sur la
figure, que l'énergie mécanique se conserve dans cette phase et a une
valeur proche de 6,7 mJ.
A t = 0,29 s: Ep =2,8 mJ, Ec =4 mJ, Em = 6,8 mJ.
A t = 0,27 s: Ep =1,3 mJ, Ec =5,4 mJ, Em = 6,7 mJ.
Q.14. Determiner la hauteur du rebond de la balle. Commenter.
L'énergie cinétique étant nulle : 6,7 10-3 = mgh avec m = 2,7 10-3 kg.
h = 6,7 /(2,7 x9,81)=0,25 m en accord avec le réglement.
|
...
|
....
|
3. Vitesse d'un coup droit smashe au tennis de table
Pour améliorer la rapidité de son coup droit, un
joueur se munit à l'entraînement d'un cinémomètre, appareil qui mesure
la vitesse d'un objet, par effet Doppler.
Pour que la mesure de la
vitesse soit la meilleure possible, ii est nécessaire de placer
l'appareil de mesure sur la partie opposée de la table face au joueur.
Le cinémomètre utilise une onde électromagnetique monochromatique. II est constitue :
- d'un emetteur qui génère une onde de fréquence f0 = 24, 125 GHz en direction de la balle (1 GHz= 109 Hz) ;
- d'un recepteur qui reçoit l'onde apres réflexion sur la balle à la fréquence fR.;
- d'une chaine de traitement électronique qui compare le signal émis et le signal reçu.
On note Df le décalage Doppler mesure par l'appareil lors de son utilisation.
Donnees:
- !'expression de la valeur absolue du décalage Doppler en fonction de
la vitesse v de la balle, la celerite Conde de l'onde electromagnetique
et la fréquence f0 générée par l'émetteur :
|Df| =2 f0 v / conde.
Q.15. Expliquer pourquoi la situation illustre l'effet Doppler.
Q.16. Déterminer le signe du décalage Doppler dans la situation ou la balle smashee s'approche du cinémomètre.
L'émetteur
émet une onde continue qui est réfléchie par toute cible se trouvant
dans la direction pointée. Par effet Doppler, cette onde réfléchie
possède une fréquence légèrement différente de celle émise, une plus
grande fréquence pour les véhicules s’approchant du radar et une plus
petite pour ceux s’en éloignant.
Suite au smash réaliseé par un joueur amateur, l'appareil mesure un décalage Doppler dont la valeur absolue est 4470 Hz.
Q.17. Calculer la vitesse de ce smash.
v = |Df| conde/(2 f0 )=4470 x 3 108 /(2 x24,125 109)=27,8 m /s.
Le record du monde du smash le plus rapide a été établi en 2003 par Mark Brandt avec une vitesse atteinte de 112,5 km·h-1.
Q.18. lndiquer, en justifiant, si la vitesse du smash du joueur amateur est du même ordre de grandeur que le record du monde.
27,8 x3,6 =100 km /h.
Ces deux vitesses sont du même ordre de grandeur.
|
ane.
|
|
|