Mathématiques,
bac Amérique du
nord 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
. |
..
..
......
...
|
Un jeu vidéo
récompense par un objet tiré au sort les joueurs ayant remporté un défi.
L’objet tiré peut être « commun » ou « rare ». Deux types d’objets
communs ou rares sont disponibles, des épées et des boucliers.
Les concepteurs du jeu vidéo ont prévu que :
- la probabilité de tirer un objet rare est de 7%;
- si on tire un objet rare, la probabilité que ce soit une épée est de
80%;
- si on tire un objet commun, la probabilité que ce soit une épée est
de 40%.
Les parties A et B sont indépendantes.
Partie A
Un joueur vient de remporter un défi et tire au sort un objet. On note :
• R l’évènement « le joueur tire un objet rare »;
• E l’évènement « le joueur tire une épée »;
• R et E les évènements contraires des évènements R et E.
1. Dresser un arbre pondéré modélisant la situation, puis calculer P(R
∩E).
2. Calculer la probabilité de tirer une épée.
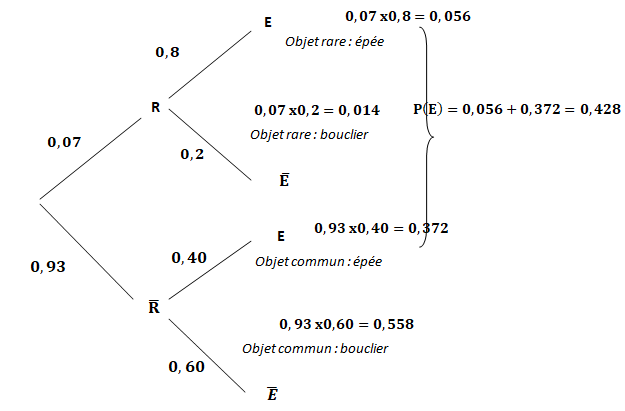
3. Le joueur a tiré une épée. Déterminer la probabilité que ce soit un
objet rare. Arrondir le résultat au millième.
PE(R) = P(E n R) / P(E) = 0,056 / 0,428 =0,131.
Partie B
Un joueur remporte 30 défis.
On
note X la variable aléatoire correspondant au nombre d’objets rares que
le joueur obtient après avoir remporté 30 défis. Les tirages successifs
sont considérés comme indépendants.
1.
Déterminer, en justifiant, la loi de probabilité suivie par la variable
aléatoire X. Préciser ses paramètres, ainsi que son espérance.
Les tirages sont indépendants et conduisent à deux issues : un
objet rare ou un objet commun. On répète 30 fois la même expérience de Bernoulli. X suit une loi binomiale de paramètres n
= 30 et p = 0,07.
Espérance E = np = 30 x0,07= 2,1.
2. Déterminer P(X < 6). Arrondir le résultat au millième.
P(X < 5) =0,984.
3. Déterminer la plus grande valeur de k telle que P(X > k) > 0,5. Interpréter le résultat dans le contexte de l’exercice.
P(X > k) = 1- P(X < k) = 0,5 ; P(X < k) =0,5 ; k=2.
4.
Les développeurs du jeu vidéo veulent proposer aux joueurs d’acheter un
« ticket d’or » qui permet de tirer N objets. La probabilité de tirer
un objet rare reste de 7%.
Les développeurs aimeraient qu’en achetant un ticket d’or, la
probabilité qu’un joueur obtienne au moins un objet rare lors de ces N
tirages soit supérieure ou égale à 0,95.
Déterminer le nombre minimum d’objets à tirer pour atteindre cet objectif. On veillera à détailler la démarche mise en oeuvre.
On
note Y la variable aléatoire comptant le nombre d'objets rares obtenus
lorsqu'un joueur tire N objets. Y suit une loi binomiale de paramètres
N et p = 0,07.
P(Y > 1) > 0,95 ; 1-P(Y=0) > 0,95 ; P(Y =0) < 0,05 ; 0,93N < 0,05 ;
N ln(0,93) < ln(0,05) ; N > ln(0,05) /ln(0,93) ; N > 42.
QCM.
1. On considère les points A(1; 0; 3) et B(4; 1; 0).
Une représentation paramétrique de la droite (AB) est :
Coordonnées du vecteur AB : (3 ; 1 ; -3 )
x= 3t+xA = 3t+1 ; y = t+yA = t ; z = -3t +zA =-3t+3 avec t réel. Réponse C.
On considère la droite (d) de représentation paramétrique
x = 3+4t
y = 6t
z = 4−2t avec t réel.
2. Parmi les points suivants, lequel appartient à la droite (d) ?
a. M(7; 6; 6) b. N(3; 6; 4) c. P(4 ; 6 ; −2) d. R(−3 ; −9 ; 7).
xM =7 =3+4t ; t =1 ; yM = 6 ; zM =4-2=2 diffère de 6.
xN =3 =3+4t ; t =0 ; yN = 0 diffère de 6.
xP =4 =3+4t ; t =0,25 ; yP = 1,5 diffère de 6.
xR =-3 =3+4t ; t =-1,5 ; yR = -9 ; zR =4+3=7.
3. On considère la droite (d′) de représentation paramétrique
x = −2+3k
y = −1−2k
z = 1+k avec k réel.
Les droites (d) et (d′) sont :
a. sécantes ; b. non coplanaires ; c. parallèles ; d. confondues.
Coordonnées d'un vecteur directeur de (d) : (4 ; 6 ; -2).
Coordonnées d'un vecteur directeur de (d') : (3 ; -2 ; 1).
Ces droites ne sont pas pârallèles, ni confondues.
Dans l'hypothèse où elles sont sécantes : -2+3k =3+4t ; k = 5 /3 +4 t/3.
-1-2k = -1-5/3-8t/3 ; -8/3-8t/3=-8/3(1+t) = 6 t ; 1+t=-9t/4 ; t = -13 /4 ; k = 5 /3 -13 /3= -8/3.
z = 4-2t=4+13 /2=21 /2.
z = 1+k=1-8/3=-5/3 diffère de 21 /2. L'hypothèse est fausse.
Les droite n'étant ni sécantes, ni parallèles , elles sont non coplanaires.
4. On considère le plan (P) passant par le point I(2; 1; 0) et perpendiculaire à la droite d.
(d).Une équation du plan (P) est :
a. 2x +3y −z −7 =0 ; c. −x + y −4z +1 =0 ; b. 4x +6y −2z +9 =0 ; d. 2x + y +1 = 0.
Coordonnées d'un vecteur directeur de la droite (d) : 4 ; 6 ; -2.
Equation du plan : 4x+6y-2z+d=0.
4xI+6yI-2zI+d=0 ; 8+6+d=0 ; d = -14.
2x+3y-z-7=0.
|
...
|
....
|
Le but de cet exercice est d’étudier la fonction [ définie sur l’intervalle ]0 ; +∞[ par :
f (x) = x ln(x2)−1 /x.
Partie A : lectures graphiques.
On a tracé ci-dessous la courbe représentative (Cf ) de la fonction f ,
ainsi que la droite (T ), tangente à la courbe (Cf ) au point A
(1 ; −1).
Cette tangente passe également par le point B(0 ; −4).
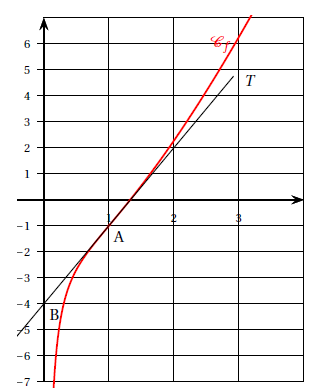
1. Lire graphiquement f ′(1) et donner l’équation réduite de la tangente (T ).
f '(1)=3. y = 3 x+b ; A(1 ; -1) appartient à la tangente :-1 = 3+b ; b = -4.
y = 3x-4.
2. Donner les intervalles sur lesquels la fonction f semble convexe ou concave.
Convexe : les tangentes sont en dessous de Cf : ]1 ; +oo[.
Concave : ]0 ; 1[.
Que semble représenter le point A pour la courbe (Cf ) ?
A est un point d'inflexion.
Partie B : étude analytique
1. Déterminer, en justifiant, la limite de f en +∞, puis sa limite en 0.
En +oo : 1 /x tend vers zéro et x ln(x2) tend vers plus l'infini ; f(x) tend vers +oo.
en zéro : -1/x tend vers -oo ; x ln(x2) tend vers zéro ; f(x) tend vers -oo.
2. On admet que la fonction f est deux fois dérivable sur l’intervalle ]0 ; +∞[.
a. Déterminer f ′(x) pour x appartenant à l’intervalle ]0 ; +∞[.
Dérivée de x ln(x2) : on pose u = x ; u' = 1 ; v=ln(x2) ; v' = 2x / x2 = 2 /x.
u'v+v'u = ln(x2)+2 ; f '(x) = ln(x2)+2+1/x2.
b. Montrer que pour tout x appartenant à l’intervalle ]0 ; +∞[,
f ′′(x) =2(x +1)(x −1) /x3 .
f "(x) = 2x /x2-2/x3 =2(x2-1)/x3=2(x +1)(x −1) /x3 .
3. a. Étudier la convexité de la fonction f sur l’intervalle ]0 ; +∞[.
f "(x) < 0 sur ]0 ; 1[, f(x) est concave.
f "(x) >0 sur ]1 ; +oo[ ; f(x) est convexe.
b. Étudier les variations de la fonction f ′, puis le signe de f ′(x) pour x appartenant à l’intervalle ]0 ; +∞[.
En déduire le sens de variation de la fonction f sur l’intervalle ]0 ; +∞[.
f "(x) < 0 sur ]0 ; 1[, f '(x) est strictement décroissante.
f "(x) >0 sur ]1 ; +oo[ ; f '(x) est strictement croissante.
f '(x) atteint un minimum en x = 1 ; f '(1) =3. Donc f '(x) > 0 et f(x) est strictement croissante.
4. a. Montrer que l’équation f (x) =0 admet une unique solution a sur l’intervalle ]0 ; +∞[.
f(x) est continue car dérivable et strictement croissante sur ]0 ; +oo[ de -oo à +oo.
0 appartient à ]-oo ; +oo[ D'après le théorème de la bijection, l'équation f(x) = 0 admet une solution unique sur ]0 ; +oo[.
b. Donner la valeur arrondie au centième de a et montrer que a vérifie : a2 = exp(1/a2).
La calcumlatrice conduit à a ~1,33.
f(a) = 0 ; a ln(a2)=1 /a ; ln(a2)=1 /a2 ; a2 = exp(1/a2).
Exercice 4. 6 points.
Pour tout entier naturel n, on considère les intégrales suivantes :
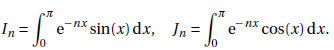
1. Calculer I0.
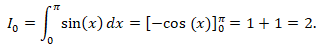
2. a. Justifier que, pour tout entier naturel n , on a In >0.
exp(-nx) >0 ; pour x appartenant à [0 ; p], sin(x) >0.
Pour tout réel x appartenant à [0 ; p], exp(-nx)sin(x) >0 ;
par positivité de l'intégrale, In >0.
b. Montrer que, pour tout entier naturel n , on a In+1−In < 0.
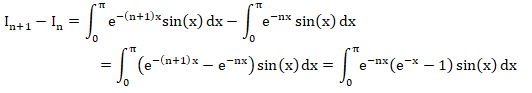
Pour tout x appartenant à [0 ; p], e-nx >0, e-x < 1 et sin(x) >0.
e-nx (e-x-1)sin(x) < 0.
On intègre sur un intervalle croissant ; par croissance de l'intégrale In+1−In < 0.
c. Déduire des deux questions précédentes que la suite (In) converge.
Cette suite est décroissante et minorée par 0, donc elle converge.
3. a. Montrer que, pour tout entier naturel n , on a la relation suivante :
Pour tout x appartenant à [0 ; p], sin(x) < 1.
Pour tout entier n : e-nx sin(x) < e-nx .
En intégrant sur un intervalle croissant, par croissance de l'intégrale : 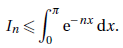
b. Montrer que, pour tout entier naturel n >1, on a :
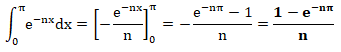
c. Déduire des deux questions précédentes la limite de la suite (In).
0 < In < (1-e-np) / n ;
en +oo, e-np tend vers zéro ; (1-e-np) / n tend vers zéro.
D'après le théorème des gendarmes, en +oo, In tend vers zéro.
4. a. En intégrant par parties l’intégrale In de deux façons différentes, établir les deux relations suivantes, pour tout entier naturel n >1 :
On pose u = e-nx et v = -cos(x) ; u' = -n e-nx ; v' = sin(x).
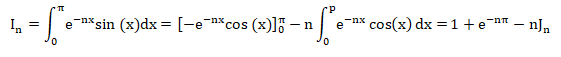
On pose v = -e-nx / n et u = sin(x) ; v' = e-nx ; u' = cos(x).
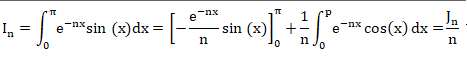
b. En déduire que, pour tout entier naturel n >1, on a : In =(1+e−np)/(n2+1).
In = 1+e-np -nJn =1+e-np -n2In ; In(1+n2)=1+e-np ; In =(1+e−np)/(n2+1).
5. On souhaite obtenir le rang n à partir duquel la suite (In) devient inférieure à 0,1.
Recopier et compléter la cinquième ligne du script Python ci-dessous avec la commande appropriée.

|
ane.
|
|
|