Observation d'un volcan par interférométrie satellitaire radar, bac Amérique du nord 2024 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Etude du mouvement orbital du satellite ALOS. ALOS est placé sur une orbite polaire (c'est-à-dire passant à la verticale des pôles terrestres) supposée circulaire dans le référentiel géocentrique à une altitude h = 692 km. Le satellite se déplace à une vitesse proche de 2,7 x 104 km-h-1. En utilisant les données d'altitude et de période du satellite, un programme écrit en langage python a permis de déterminer les positions du satellite sur son orbite à intervalle de temps régulier t = 369,3 s et de représenter les vecteurs vitesse et variation de vitesse du satellite en ces points. Q.1. Indiquer les lignes du programme fourni qui permettent de calculer les coordonnées approchées des vecteurs variation de vitesse. 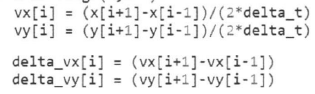Q.2. Indiquer lequel des deux vecteurs représentés à une position du satellite donnée correspond au vecteur variation de vitesse. Justifier. 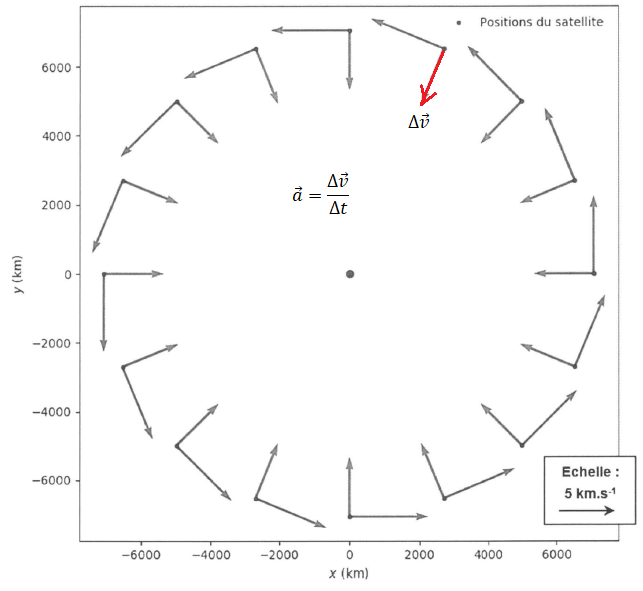Le vecteur vitesse est tangent à la trajectoire. La norme du vecteur vitesse étant constante, le mouvement est uniforme. Le vecteur accélération est dirigé vers le centre de la terre. Q.3. Montrer à l'aide de l'échelle fournie que la valeur de l'accélération moyenne du satellite est voisine de 8 m s-2. a = v2 / (R+h )=(2,7 104/3,6)2 / (6,37 106 +6,92 105)~8 m s-2. Le mouvement du centre de masse, S, du satellite ALOS est étudié dans le référentiel géocentrique supposé galiléen en utilisant le repère de Frenet. La masse du satellite est notée m. Q.4. Exprimer, dans le repère de Frenet, la force d'interaction gravitationnelle exercée par la Terre sur le satellite ALOS en fonction de G, m, Mt, Rt, z. Représenter, sans souci d'échelle, cette force sur un schéma avec le repère de Frenet associé au satellite. 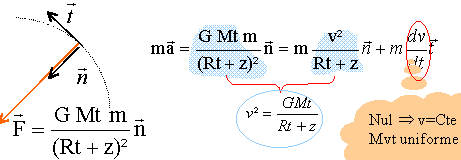Q.5. Établir l'expression du vecteur accélération du satellite et calculer sa norme. Comparer à la valeur obtenue à la question Q.3. a =6,67 10-11 x5,97 1024 /(6,37 106 +6,92 105)2 ~ 8 m s-2. Q.6. Montrer que le mouvement du satellite est uniforme et établir l'expression de sa vitesse. Q.7. En déduire l'expression de la période de révolution du satellite en fonction de G, M, Rt, z. Calculer sa valeur. Le satellite décrit la circonférence 2 p(Rt+z) à la vitesse v durant la période T. T = 2 p(Rt+z) / v =6,28 x(6,37 106 +6,92 105) / (2,7 104 /3,6) =5,9 103 s. Compte tenu de la rotation de la Terre sur elle-même, le satellite repasse tous les 46 jours à la verticale d'un même point de la surface terrestre. Q.8. Déterminer le nombre d'orbites parcourues par le satellite ALOS avant de repasser au-dessus du même point. 46 x24 x3600 / (5,9 103)=6,7 102. ... .... 2. Étude de la déformation du sol par interférométrie radar Un satellite faisant de l'interférométrie radar est dit actif: il éclaire lui-même un point de la surface terrestre qu'il observe en émettant une onde radar et récupère le signal renvoyé. L'interférométrie satellitaire radar (lnSAR) est une technique d'imagerie utilisée principalement pour détecter des mouvements de terrain comme la contraction ou le gonflement des sols argileux et le suivi de l'activité des volcans. Q.9. Écrire la relation entre la longueur d'onde, la célérité et la période de l'onde, en précisant les unités de ces grandeurs. l = c T. Longueur d'onde (m) ; célérité (m/s) ; période (s). Q.10. Justifier, à l'aide du document ci-dessous, que les ondes émises par le satellite ALOS dont la longueur d'onde est 23,6 cm appartiennent au domaine des ondes radio. T = 0,236 / (3 108) =7,87 10-10 s. f = 1 / T =1,3 109 Hz. Le principe de la mesure de déplacement par lnSAR est le suivant : le satellite capte une image de l'ensemble des points d'une même zone de la Terre depuis la même position dans le ciel à deux dates différentes. Une contraction ou un gonflement du sol survenant entre ces deux dates induit une variation de la distance entre le satellite et le sol. Cette variation génère une différence de marche entre les deux ondes radar reçues. Une figure d'interférences, appelée interférogramme, est obtenue par traitement informatique. L'interférogramme réalisé permet de mesurer le déplacement du sol dans l'axe de visée du satellite. On admettra que la variation d'altitude du sol est due uniquement à une contraction de ce dernier. On note L la distance entre le satellite et le point visé à la surface de la Terre lors du premier passage et d le déplacement du sol dans l'axe de visée du satellite entre le premier et le deuxième passage du satellite. Q.11. En exprimant la distance parcourue par l'onde radar lors du premier passage et celle parcourue par l'onde lors du deuxième passage, établir que la relation entre la différence de marche d entre ces deux ondes et le déplacement du sol d est : d= 2d. Lors du premier passage : 2 L = c t1 ; lors du second passage : 2(L+d)= c t2 ; t2-t1 = 2d / c ; d= 2d. Q.12. En déduire que la relation entre le déplacement du sol d et la longueur d'onde l pour que ces deux ondes soient en phase est : d= k l /2 avec k entier. Si la différence de marche est égale à un nombre entier de longueur d'onde, les ondes sont en phase : 2d = k l ; d= k l /2 avec k entier. Du 30 mars au 1° avril 2007, le volcan situé sur l'ile de la Réunion a connu une crise éruptive. Cet évènement a été imagé par le satellite radar ALOS dont la longueur d'onde de travail est de 23,6 cm. L'analyse comparée des deux images (Jour 1 et Jour 46) a permis la construction d'un interférogramme. Sur la figure , les franges les plus claires correspondent à des interférences constructives. Q.13. Déterminer l'entier k entre les points A et B et en déduire la variation d'altitude du point B en supposant que le point A n'a pas subi de déplacement. k = 6 ; d= k l /2 =3 x 0,236=0,708 m. ane.

menu