Mathématiques, Bac Amérique du Sud 2024.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Exercice 1 (5 points)
Voici la répartition des principaux groupes sanguins des habitants de France :

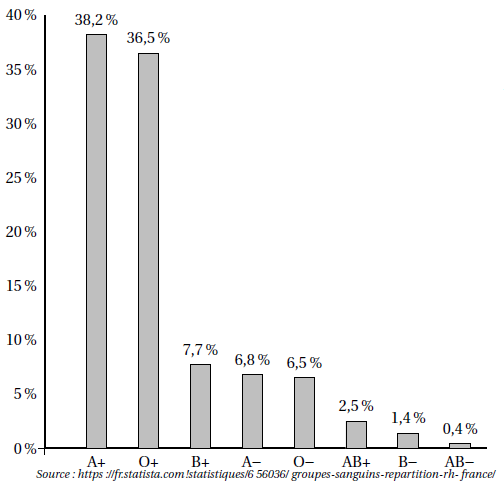
A+, O+, B+, A−, O−, AB+, B− et AB− sont les différents groupes sanguins combinés aux rhésus.
Par exemple : A + est le groupe sanguin A de rhésus +.
Une expérience aléatoire consiste à choisir une personne au hasard dans la population française et à déterminer son groupe sanguin et son rhésus.
Dans l’exercice, on adopte les notations du type :
A + est l’évènement « la personne est de groupe sanguin A et de rhésus + »
A− est l’évènement « la personne est de groupe sanguin A et de rhésus −»
A est l’évènement « la personne est de groupe sanguin A »
Les parties 1 et 2 sont indépendantes.
Partie 1.
On note Rh + l’évènement « La personne est de rhésus positif ».
1. Justifier que la probabilité que la personne choisie soit de rhésus positif est égale à 0,849.
(38,2 +36,5 +7,7 +2,5) / 100 =0,849.
2. Démontrer à l’aide des données de l’énoncé que PRh+(A) = 0,450 à 0,001 près.
PRh+(A) =P(Rh+) n P(A) / P(Rh+) = 0,382 / 0,849=0,450.
3. Une personne se souvient que son groupe sanguin est AB mais a oublié son rhésus. Quelle est la probabilité que son rhésus soit négatif ? Arrondir le résultat à 0,001 près.
0,4 / (2,5+0,4)=0,138.
PARTIE 2
Dans cette partie, les résultats seront arrondis à 0,001 près.
Un donneur universel de sang est une personne de groupe sanguin O et de rhésus négatif.
On rappelle que 6,5% de la population française est de groupe O−.
1. On considère 50 personnes choisies au hasard dans la population française et on note X la variable aléatoire qui compte le nombre de donneurs universels.
a. Déterminer la probabilité que 8 personnes soient des donneurs universels. Justifier votre réponse.
Ce choix peut être assimilé à un tirage avec remise. X compte le nombre de donneurs universels ; X suit la loi binomiale de paramètres n = 50 et p = 0,065.
p(X=8) = (50 8) x0,0658 x(1-0,065)50-8 ~0,010.
 b. On considère la fonction ci-dessous nommée proba d’argument k écrite en langage Python.
def proba(k) :
p=0
for i in range(k+1) :
p = p + binomiale(i,50,0.065)
return p
Cette fonction utilise la fonction binomiale d’argument i ,n et p, créée pour l’occasion, qui renvoie la valeur de la probabilité P(X = i ) dans le cas où X suit une loi binomiale de paramètres n et p.
Déterminer la valeur numérique renvoyée par la fonction proba lorsqu’on saisit proba(8) dans la console Python. Interpréter ce résultat dans le contexte de l’exercice.
La valeur numérique renvoyée correspond à P(X< 8) ~0,995.
Sur 50 personnes, la probabilité qu'il y ait au plus 8 personnes de groupe O- est égale à 0,995.
2. Quel est le nombre minimal de personnes à choisir au hasard dans la population française pour que la probabilité qu’au moins une des personnes choisies soit donneur universel, soit supérieure à 0,999.
P(X >1) >0,999 ; 1-P(X=0) >0,999.
P(X=0) =(n 0) x0,0650 x(1-0,065)n =0,935n.
1-0,935n >0,999 ; 0,001 >0,935n ; ln(0,001) > n ln(0,935) ;
n > ln(0,001) / ln(0,935) ; n >102,8 ; n =103.

Exercice 2 5 points
Cet exercice contient 5 affirmations.
Pour chaque affirmation, répondre par VRAI ou FAUX en justifiant la réponse.
Toute absence de justification ou justification incorrecte ne sera pas prise en compte dans la notation.
Partie 1
On considère la suite (un) définie par :
u0 = 10 et pour tout entier naturel n, un+1 =un/3 +2.
1. Affirmation 1 : La suite (un) est décroissante minorée par 0. Vrai.
Initialisation : u1=10/3 +2=16/3 < 10. La proposition est vraie au rang zéro.
Hérédité : 0 < un+1 < un est supposée vraie.
0 < un+1 / 3< un /3 ; 2 < un+1 / 3+2 < un /3+2 ; 2 < un+2  < un+1.
La proposition est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n.
 2. Affirmation 2 : quand n tend vers +oo, un tend vers zéro. Faux.
D'après la question précédente 2 < un+2 .
3. Affirmation 3 : La suite (vn) définie pour tout entier naturel n par vn = un −3 est géométrique. Vrai.
vn+1 = un +1−3=un/3+2-3=un/3 -1 =1/3 (un-3)=vn/3.
Partie 2
On considère l’équation différentielle (E) : y′ =1,5y +2.d’inconnue y, fonction définie et dérivable sur R
1. Affirmation 4 : Il existe une fonction constante solution de l’équation différentielle (E). Vrai.
g(x) = constante = A ; g '(x) =0.
Repport dans (E) :0 = 1,5A +2 ; A = -2 /1,5 = -4 /3.
2. Dans un repère orthonormé  on note Cf la courbe représentative de la fonction f solution de (E) telle que f (0) =0.
3. Affirmation 5 : La tangente au point d’abscisse 1 de Cf a pour coefficient directeur 2exp(1,5). Vrai.
Solution générale de y'-1,5y = 0 : y = B exp(1,5x) avec A une constante réelle.
Solution générale de (E) : f(x) = B exp(1,5x) -4/3.
f(0) = B-4,3 = 0 ; B = 4/3.
f(x) =4/3 (exp(1,5x)-1).
f '(x) = 2 exp(1,5x) ; f '(1) = 2 exp(1,5).
 

...
....
Exercice 3 5 points
Partie 1
On considère la fonction f définie sur l’ensemble des nombres réels R par :
f (x) =(x2−4)e−x .
On admet que la fonction f est dérivable sur R et on note f ′ sa fonction dérivée.
1. Déterminer les limites de la fonction f en −∞ et en +∞.
En -oo : x2 tend vers +oo ; e-x tend vers +oo ; par produit de limites, f(x) tend vers +oo.
En +oo : x2 tend vers +oo ; e-x tend vers zéro ; par produit des limites, f(x) tend vers zéro.
2. Justifier que pour tout réel x, f ′(x)=(−x2+2x +4)e−x .
On pose u = x2-4 et v = e-x ; u' = 2x ; v' = -e-x.
u'v+v'u = 2xe-x-(x2-4)e-x=(−x2+2x +4)e−x .
 3. En déduire les variations de la fonction f sur R.
e−x > 0 ; le signe de f'(x) est celui de −x2+2x +4.
D =4+16=20=(2x5½)2.
x1 = (2 -2x5½) / 2=(1 -5½) ; x2 = (2+2x5½) / 2=(1 +-5½).

 Partie 2
On considère la suite (In) définie pour tout entier naturel n par
1. Justifier que I0 = e2−1.
I0 = [-e-x]-20= -1+e2.
2. En utilisant une intégration par partie, démontrer l’égalité :
In+1 = (−2)n+1e2+(n +1)In.
On pose u' =xn et v= e-x ; u =xn+1 /(n+1) ; v' = -e-x.


3. En déduire les valeurs exactes de I1 et de I2.
I1 = I0+(-2)e2 =-1+e2.-2e2= -1-e2.
I2 =2I1+4e2= -2+2e2.
 Partie 3
1. Déterminer le signe sur R de la fonction f définie dans la partie 1.
ex >0 ; f(x) a le signe de x2-4.
f(x) >0 si x appartient = ]-oo ; -2[ union ]2 ; +oo[.
f(x) = 0 si x = -2 et x = +2.
f(x) < 0 si x appartient à ]-2 ; +2[.
2. On a représenté la courbe Cf de la fonction f dans un repère orthonormé
Le domaine D du plan hachuré est délimité par la courbe Cf , l’axe des abscisses et l’axe des ordonnées.
Calculer la valeur exacte, en unité d’aire, de l’aire S du domaine D.



Exercice 4 5 points
L’espace est muni d’un repère orthonormé.
On considère les trois points A(3; 0; 0), B(0; 2; 0) et C(0; 0; 2).
« Le carré de l’aire du triangle ABC est égal à la somme des carrés des aires des trois autres
faces du tétraèdre OABC »,
Partie 1 : Distance du point O au plan (ABC)
1. Démontrer que le vecteur n (2 ; 3 ; 3) est normal au plan (ABC).
On montre que le vecteur n est perpendiculaire à deux vecteurs non colinéaires du plan (ABC).

2. Démontrer qu’une équation cartésienne du plan (ABC) est : 2x +3y +3z −6 = 0.
2x+3y+3z+d=0.
A appartient à ce plan : 2*3+0+0+d = 0 ; d = -6.
Equation de ce plan : 2x +3y +3z −6 = 0.
3. Donner une représentation paramétrique de la droite d passant par O et de vecteur directeur n .
x =2t ; y = 3t ; z = 3t avec t réel.
4. On note H le point d’intersection de la droite d et du plan (ABC).
Déterminer les coordonnées du point H.
 2xH +3yH +3zH −6 = 0.
4t +9t +9t-6=0 ; t = 6/22=3/11.
H(6 /11 ; 9/11 ; 9 /11).
 5. En déduire que la distance du point O au plan (ABC) est égale à 3x22½ /11.
OH2 =(6/11)2 +(9 /11)2 +(9/11)2 =198 / 121=9 x22 / 112.  OH = 3x22½ /11.
Partie 2 : Démonstration de la propriété.

1. Démontrer que le volume du tétraèdre OABC est égal à 2.
Aire de la base, triangle OAB : OA x OB / 2 = 3 x2 / 2 = 3.
Hauteur relative à ce triangle OC = 2.
Volume de ce tétraèdre = aire de base x hauteur / 3 = 3x2 /3 = 2.
 2. En déduire que l’aire du triangle ABC est égale à 22½.
Volume du tétraèdre = aire triangle ABC x hauteur OH / 3 = aire triangle ABC x22½ /11.
aire triangle ABC =2 x11 / 22½ =22½.
3. Démontrer que pour le tétraèdre OABC, « le carré de l’aire du triangle ABC est égal à la somme des carrés des aires des trois autres faces du tétraèdre ».
Carré de l’aire du triangle ABC =22.
Aire triangle OAB = OA xOB / 2 = 3.
Aire du triangle OAC = OA x OC / 2 =3.
Aire du triangle OBC = OB x OC / 2 = 2.
32 +32 +22 = 22.






  
menu