Mathématiques, Bac Amérique du Sud 2024. .

Exercice 1 (5 points)
Partie A.
On considère l’équation différentielle
(E) : y′+0,25 y =20 exp(-0,25x).
d’inconnue y, fonction définie et dérivable sur l’intervalle [0 ; +∞[.
1. Déterminer la valeur du réel a tel que la fonction g définie sur l’intervalle [0 ; +∞[ par g(x) = ax exp(-0,25x) soit une solution particulière de l’équation différentielle (E).
Calcul de g'(x) en posant u = ax et v = exp(-0,25x).
u' = a ; v' = -0,25 exp(-0,25x) ;
u'v+v'u = a exp(-0,25x)-0,25ax exp(-0,25x) = a(1-0,25x) exp(-0,25x).
Repport dans (E) : a(1-0,25x) exp(-0,25x) +0,25 ax exp(-0,25x)=20 exp(-0,25x).
a(1-0,25x) =20 ; pour x = 0, a = 20.
g(x) = 20x exp(-0,25x).
2. On considère l’équation différentielle
(E′) : y′ +0,25y = 0 d’inconnue y, fonction définie et dérivable sur l’intervalle [0 ; +∞[.
Déterminer les solutions de l’équation différentielle (E′).
y = A exp(-0,25x) avec A une constante réelle.
3. En déduire les solutions de l’équation différentielle (E).
f(x) = (20 x +A) exp(-0,25x).
4. Déterminer la solution f de l’équation différentielle (E) telle que f (0) = 8.
f(0)=A=8.
f(x) = (20x+8) exp(-0,25x).
PARTIE B
On considère la fonction f définie sur l’intervalle [0 ; +∞[ par
f (x) =(20x +8) exp(-0,25x).
On admet que la fonction f est dérivable sur l’intervalle [0 ; +∞[ et on note f ′ sa fonction
dérivée sur l’intervalle [0 ; +∞[. De plus, on admet que en plus l'infini f(x) tend vers zéro.
1. a. Justifier que, pour tout réel x positif,
f ′(x) =(18−5x) exp(-0,25x).
On pose u = 20+5x et v = exp(-0,25x) ; u' = 20 ; v' = -0,25 exp(-0,25x).
u'v+v'u = 20 exp(-0,25x) -0,25(20x+8) exp(-0,25x) = (18−5x) exp(-0,25x).
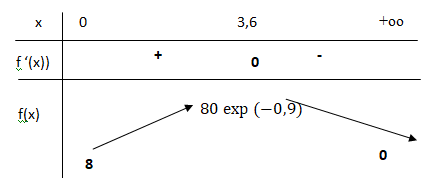
b. En déduire le tableau de variations de la fonction f . On précisera la valeur exacte du maximum de la fonction f sur l’intervalle [0 ; +∞[.

2. Dans cette question on s’intéresse à l’équation f (x) = 8.
a. Justifier que l’équation f (x) = 8 admet une unique solution, notée a, dans l’intervalle [14; 15].
Sur cet intervalle, la fonction f est continue car dérivable et strictement décroissante.
f(14) =288 exp(-0,9) ~8,7.
f(15) = 308exp(-3,75)~7,24.
8 appartient à l(intervalle [f(15) ; f(14) ].
D'après le corollaire du théorème des valeurs intermédiaires, il existe un unique réel a tel que f(a) = 8.
b. Recopier et compléter le tableau ci-dessous en faisant tourner étape par étape la fonction solution_equation ci-dessous, écrite en langage Python.
frommath import exp
def f(x) :
return (20*x+8)*exp(-1/4*x)
def solution_equation() :
a,b = 14,15
while b-a > 0.1 :
m= (a+b)/2
if f(m) > 8 :
a =m
else :
b =m
return a,b

a	14	14	14,25	14,375	14,4375
b	15	14,5	14,5	14,5	14,5
b-a	1	0,5	0,25	0,125	0,0625
m	14,5	14,25	14,375	14,4375
Condition f(m) > 8	Faux	Vrai	Vrai	Vrai

c. Quel est l’objectif de la fonction solution_equation dans le contexte de la question ?
Déterminer par dichotomie, un encadrement d'amplitude 0,1 de la solution de l'équation f(x) = 8 dans l'intervalle [14 ; 15].

Exercice 2 6 points
On dispose de deux urnes opaques U1 et U2.
L’urne U1 contient 4 boules noires et 6 boules blanches.
L’urne U2 contient 1 boule noire et 3 boules blanches.
On considère l’expérience aléatoire suivante :
On pioche au hasard une boule dans U1 que l’on place dans U2, puis on pioche au hasard une boule dans U2.
On note :
• N1 l’évènement « Piocher une boule noire dans l’urne U1 ».
• N2 l’évènement « Piocher une boule noire dans l’urne U2 ».
PARTIE A
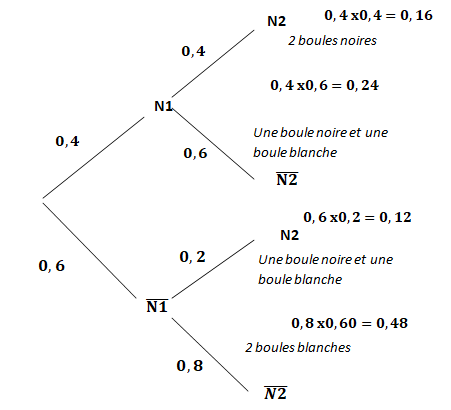
1. On considère l’arbre de probabilités ci-dessous..
a. Justifier que la probabilité de piocher une boule noire dans l’urne U2 sachant qu’on a pioché une boule blanche dans l’urne U1 est 0,2.
L'urne U2 contient alors 4 boules blanches et une boule noire.
Probabilité de piocher une boule noire dans l’urne U2 :1 / 5 = 0,2.
b. Compléter l’arbre de probabilités en faisant apparaître sur chaque branche les probabilités des évènements concernés,
sous forme décimale.

2. Calculer la probabilité de piocher une boule noire dans l’urne U1 et une boule noire dans l’urne U2.
L'urne U2 contient alors 3 boules blanches et 2 boules noires.
Probabilité de piocher une boule noire dans l’urne U2 :2 / 5 = 0,4.
3. Justifier que la probabilité de piocher une boule noire dans l’urne U2 est égale à 0,28.
Formule des probabilités totales : P(N1 n N2) = P(N1) x P(N2) + P(non N1 n N2) = 0,16 +0,12 = 0,28.
4. On a pioché une boule noire dans l’urne U2.
Calculer la probabilité d’avoir pioché une boule blanche dans l’urne U1. On donnera le résultat sous forme décimale arrondie à 10⁻².
P_N2(non N1) =P(N2 n Non N1) / P(N2) = 0,12 / 0,28 = 3 /7 ~0,43.
PARTIE B
n désigne un entier naturel non nul.
L’expérience aléatoire précédente est répétée n fois de façon identique et indépendante, c’est-à-dire que les urnes U1 et U2 sont remises dans leur configuration initiale, avec respectivement 4 boules noires et 6 boules blanches dans l’urne U1 et 1 boule noire et 3 boules blanches dans l’urne U2, entre chaque expérience.
On note X la variable aléatoire qui compte le nombre de fois où on pioche une boule noire dans l’urne U2.
On rappelle que la probabilité de piocher une boule noire dans l’urne U2 est égale à 0,28 et celle de piocher une boule blanche dans l’urne U2 est égale à 0,72.
1. Déterminer la loi de probabilité suivie par X. Justifier votre réponse.
On répète n fois de façon identique et indépendante une expérience qui ne possède que deux issues. X donne le nombre de succès ; X suit la loi binomiale de paramètre n et p = 0,28.
2. Déterminer par le calcul le plus petit entier naturel n tel que : 1−0,72ⁿ >0,9.
1-0,9 > 0,72ⁿ.
ln(0,1) > n ln(0,72).
n > ln(0,1) / ln(0,72) ; ln(0,1) / ln(0,72) = 7,01.
n =8.
3. Interpréter le résultat précédent dans le contexte de l’expérience.
Il faut au moins 8 tirages pour que la probabilité de piocher au moins une boule noire soit supétrieur à 0,9.

PARTIE C
Dans cette partie les urnes U1 et U2 sont remises dans leur configuration initiale, avec respectivement 4 boules noires et 6 boules blanches dans l’urne U1 et 1 boule noire et 3 boules blanches dans l’urne U2.
On considère la nouvelle expérience aléatoire suivante :
On pioche simultanément deux boules dans l’urne U1 que l’on place dans l’urne U2, puis on pioche au hasard une boule dans l’urne U2.
1. Combien y a-t-il de tirages possibles de deux boules simultanément dans l’urne U1 ?
Il y a (¹⁰₂) =10 x 9 /2 = 45 tirages possibles.
2. Combien y a-t-il de tirages possibles de deux boules simultanément dans l’urne U1 contenant exactement une boule blanche et une boule noire ?
(⁴₁) (⁶₁)= 4 x6 = 24.
3. La probabilité de piocher une boule noire dans l’urne U2 avec cette nouvelle expérience est- elle supérieure à la probabilité de tirer une boule noire dans l’urne U2 avec l’expérience de la partie A? Justifier votre réponse.
- Probabilité de tirer 2 boules noires dans U1 : P(NN) = (⁴₂) /45 = 6 /45 = 2 /15.
L'urne N2 contient alors 3 boules noires et 3 boules blanches. La probabilité de tirer une boule noire dans U2 est 3 /6 = 0,5.
- Probabilité de tirer une boule blanche et une boule noire dans U1 :
P(NB) = 24 /45=8/15.
L'urne N2 contient alors 2 boules noires et 4 boules blanches. La probabilité de tirer une boule noire dans U2 est 2 /6 = 1/3.
- Probabilité de tirer 2 boules blanches dans U1 :
P(BB) = (⁶₂) /45=15/45= 1/3.
L'urne N2 contient alors 1 boule noire et 5 boules blanches. La probabilité de tirer une boule noire dans U2 est 1 /6.
Probabilité de tirer une boule noire dans U2 est :

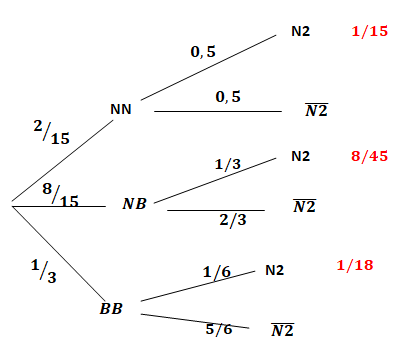
1 /15 +8 /45 +1/18 = 6 /90 +16 /90 +5 /90 = 27 /90 = 3 /10 =0,3.
Cette valeur est supérieure à la probabilité de tirer une boule noire dans l'urne U2 (0,28 expérience de la partie A).