Oxydation
ion iodure, pile de Volta, mathématiques, panneau photovoltaïque, bac
STL Nlle Calédonie 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Oxydation des ions iodure.
L'iodure de potassium est utilisé comme complément alimentaire. Il est
notamment intégré au sel de table pour prévenir les carences en iode
chez les populations ne consommant que peu de fruits de mer et de
poissons. L’exposition du sel iodé à l’air libre provoque l’oxydation
lente des ions iodure.
Au laboratoire, on met en oeuvre l’oxydation des ions iodure I–(aq)
par les ions peroxodisulfate S2O82–(aq)
pour estimer la durée de l’oxydation. On note v la vitesse de la
réaction et C la concentration du milieu réactionnel en ions
peroxodisulfate.
La concentration initiale en ions peroxodisulfate vaut C(0)=0,0042 mol·L–1
.

Couples
redox mis en jeu : I2(aq) / I–(aq) et S2O82–(aq) / SO42–(aq)
1. Écrire l’équation de la réaction modélisant
l’oxydation des ions iodure par les ions peroxodisulfate.
2I–(aq)= I2(aq) +2e-.
S2O82–(aq) +2e-= 2
SO42–(aq).
2I–(aq) +S2O82–(aq) = I2(aq) +2 SO42–(aq).
2. Donner la
définition de la vitesse de disparition v des ions peroxodisulfate en
fonction de leur concentration C.
v = -dC / dt.
3. Justifier
qualitativement, à partir du deuxième graphique, que la réaction
effectuée admet un ordre 1.
Le graphe v = f(C) est une droite passant par l'origine.
Dans la suite on note k la
constante de vitesse de la réaction.
4. En déduire
l’équation différentielle d’ordre 1 vérifiée par la concentration C en
ions peroxodisulfate.
v= -dC/dt = kC ; dC/dt + kC = 0.
5. Déterminer la
valeur de la constante de vitesse k et préciser son unité.
Coefficient directeur de la droite : k = 0,0085 s-1.
Étude
mathématique de la concentration.
Par la suite, on note C la fonction définie sur l’intervalle [0 ; +∞[
modélisant la concentration de peroxodisulfate C(t) (exprimée en mol·L–1)
en fonction du temps t (exprimé en seconde).
Pour une évolution de la concentration donnée par une relation d’ordre
1, les données physiques de l’expérience conduisent à résoudre
l’équation différentielle (E) :
y ' = − 0,0085y .
6. Déterminer la
fonction C, solution de l’équation différentielle (E) vérifiant C(0) =
0,0042.
Solution générale : C =A exp(-0,0085 t) avec A une constante.
C(0) =A =0,0042 ; C = 0,0042 exp(-0,0085 t).
7.
Résoudre l’équation C(t) = 0,00021 et donner une valeur approchée à la
seconde près de la durée nécessaire pour que la concentration
résiduelle en peroxodisulfate, correspondant à une oxydation de 95 % du
réactif limitant, soit égale à 0,00021 mol·L–1.
0,0042 exp(-0,0085 t) = 0,00021 ; exp(-0,0085 t) =0,05 ;
-0,0085 t = ln(0,05) ; t ~352 s.
Étude
d’une pile électrochimique.
La pile de Volta, ou pile voltaïque, fut la première pile électrique.
Elle a été inventée par Alessandro Volta en 1800.
La pile est faite d'un empilement de plaques circulaires de zinc [...]
et de cuivre ou d'argent [...] séparées par une couche de tissu
imprégné d'eau de préférence salée. La tension aux bornes de la pile
est proportionnelle au nombre de motifs {zinc – électrolyte – cuivre}
répétés. Source Wikipédia
Dans cet exercice, une pile de Volta est réalisée au laboratoire puis
intégrée à un circuit électrique afin d’en estimer l’autonomie dans des
conditions de fonctionnement données.
Données :
couples redox mis en jeu : Ag+(aq)/Ag(s) ; Zn2+(aq)/Zn(s)
;
constante de Faraday : F = 96 500 C·mol–1 ;
masses molaires atomiques : M(Zn) = 65,4 g·mol–1 et M(Ag)
= 107,9 g·mol–1 ;
équations de demi-réaction électronique :
- à l’électrode de zinc : Zn(s) → Zn2+(aq) + 2e– ;
- à l’électrode d’argent : Ag+(aq) + e– → Ag(s).
Étude de la demi-pile Zn2+(aq)/Zn(s).
1. Déterminer
l’oxydant et le réducteur du couple Zn2+(aq)/Zn(s)
Oxydant : Zn2+(aq) ; réducteur Zn(s).
2. Donner le nom de
la réaction qui se produit à l’électrode de zinc.
Oxydation du zinc.
3. En déduire sa
polarité ainsi que le nom donné à cette électrode.
Anode négative.
Réalisation de la pile.
On réalise la pile zinc-argent en reliant par un pont salin gélifié de
nitrate de potassium (K+(aq) ; NO3–(aq))
les deux demi-piles suivantes :
une lame de zinc de masse mZn = 5,0 g immergée dans un
volume V1 = 50 mL d’une solution de sulfate de zinc (Zn2+(aq)
; SO42–(aq)) de concentration en soluté apporté c1
= 0,20 mol·L–1 ;
une lame d’argent de masse mAg = 2,9 g immergée dans un
volume V2 = 50 mL d’une solution de nitrate d’argent (Ag+(aq)
; NO3–(aq)) de concentration en soluté apporté c2
= 0,10 mol·L–1.
4. Préciser le rôle
du pont salin.
Le
pont salin permet la continuité électrique et assure
l'électroneutralité des solutions lors du fonctionnement de la pile.
.5. Écrire
l’équation de la réaction modélisant le fonctionnement de la pile.
Zn(s) = Zn2++2e-.
2 Ag++2e-=2 Ag(s)
Zn(s) +2 Ag+= Zn2++2Ag(s).
6. Légender le
schéma de la pile.
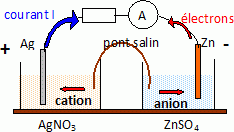
7. Calculer
la quantité de matière initiale du métal zinc ainsi que des ions argent.
n(Zn) = 5,0 / 65,4=0,076 mol = 76 mmol.
n(Ag+)=0,10 x0,050 =5 mmol.
8. Déterminer le
réactif limitant, en expliquant la démarche.
n(Zn / 1 =76 mmol ; n(Ag+)/2=2,5 mmol ( en défaut).
9. En déduire que
la quantité d’électrons disponible dans la pile est n(e–) =
5,0 x 10–3 mol.
n(e–)=n(Ag+)= 5 mmol.
Estimation de
l’autonomie de la pile.
On relève aux bornes du récepteur de résistance R = 10 ohms une tension
U = 1,1 V. On considère que la valeur de la tension reste constante
durant toute la durée de fonctionnement de la pile.
10. Calculer la
durée de fonctionnement de la pile dans les conditions décrites
ci-dessus, en heures. Commenter la valeur obtenue.
Q = n(e–) F=5,0 10-3 x96500 =482,5 C.
I = U / R =1,1 / 10 = 0,11 A.
t = Q / I =482,5 /0,11 ~4,4 103 s. Valeur très faible.
|
...
|
....
|
Étude de fonction
On considère la fonction f définie sur R par f(x)) = e-x +
0,5𝑥 − 3 dont la courbe représentative Cf est donnée dans le repère
orthonormé du plan ci-dessous.

1. Calculer la
limite de 𝑓 en +∞.
e-x tend vers zéro ; 0,5 x-3 tend vers +oo.
2. On note f
' la fonction dérivée de fsur R. Déterminerf '(0) par lecture graphique.
Coefficient directeur de la tangente à la courbe en x = 0 : -0,5.
3. Calculer f
'(𝑥) et vérifier par le calcul le résultat obtenu à la question 2.
f '(x) = -e-x+0,5 ; f '(0) = -1+0,5 = -0,5.
4. Étudier les
variations de f sur R.
f '(x) = 0 si e-x=0,5 ; -x =ln(0,5 ; x = ln(2).
Si x appartient à ]-oo ; ln(2[ : f '(x) <0 et f(x) est strictement
décroissante.
Si x appartient à ]ln 2 ; +oo[ : f '(x) >0 et f(x) est strictement
croissante.
Si x = ln(2), la fonction présente un minimum.
5. On considère le
programme Python suivant :
from math import exp
def abscisse():
x = – 1.5
while exp( – x) + 0.5 * x – 3 > 0 :
x = x + 0.01
return x
L'exécution de l’instruction abscisse() renvoie la valeur –1,29 à 10-2
près. Interpréter cette valeur dans le contexte de l’exercice.
Abscisse de A, intersection de la courbe avec l'axe des abscisses.
6. Reproduire et
modifier le programme Python précédent pour que l’exécution de
l’instruction abscisse() renvoie une valeur approchée à 10-2
près de l’abscisse du point B.
from math import exp
def abscisse():
x = 5.5
while exp( – x) + 0.5 * x – 3 < 0 :
x = x + 0.01
return x.
Étude d’un panneau
photovoltaïque
Dans une logique de respect de l’environnement et de transition
énergétique, le recours à l’énergie photovoltaïque est en plein essor.
Son usage se démocratise et les panneaux photovoltaïques font désormais
partie du quotidien. Composées d’un assemblage de matériaux permettant
de convertir efficacement l’énergie lumineuse en électricité, les
cellules photovoltaïques s’inscrivent dans le mix énergétique français
(Source CEA).
L’objectif de cet exercice est d’étudier dans un premier temps les
caractéristiques d’un panneau photovoltaïque du commerce puis d’étudier
au laboratoire son utilisation pour alimenter la résistance d’un
chauffe-eau.
Données :
conditions standard de tests : un éclairement de 1 000 W·m–2
et une température de cellule de 25 °C ;
données du fournisseur pour le panneau photovoltaïque en conditions
standard de tests (site eco-greenenergy) :
- rendement d’un panneau : 20,51 % ;
- tension à puissance maximale : Upm = 40,58 V ;
- intensité à puissance maximale : Ipm = 13,06 A ;
-tension circuit ouvert : Uco = 49,29 V ;
- intensité de court-circuit : Icc = 13,64 A.
Allure de la
caractéristique d’un panneau photovoltaïque.
1. Schématiser la
chaîne énergétique d’un panneau photovoltaïque.
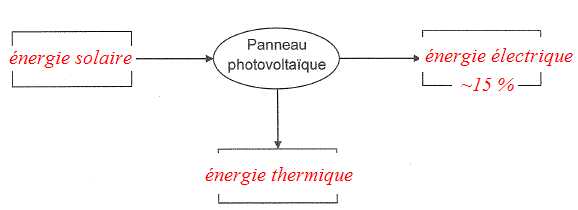
On fournit ci-dessous l’allure de la courbe caractéristique du panneau
photovoltaïque.
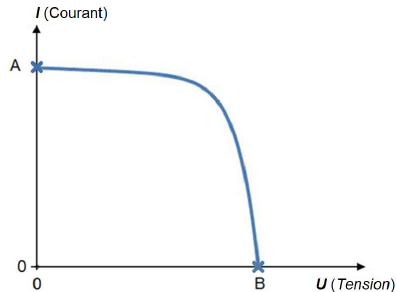
2. Identifier les
données du fournisseur du panneau photovoltaïque correspondant aux
points A et B indiqués sur l’allure ci-dessus.
A : intensité de court-circuit : Icc = 13,64 A.
B : tension circuit ouvert : Uco = 49,29 V.
3. Un panneau
photovoltaïque n’est pas une source idéale de tension. Justifier cette
affirmation en s’appuyant sur l’allure fournie.
Pour une source idéale de tension , U est constante quelle que soit
l'intensité.
4. Calculer la
puissance maximale notée Pmax, en W, fournie par ce panneau
dans les conditions standard de tests.
Upm * Ipm= 40,58 *13,06 = 530 W.
- intensité à puissance maximale : Ipm = 13,06 A ;
5. Rappeler la
relation permettant de calculer le rendement d’un panneau
photovoltaïque en fonction de la puissance maximale électrique Pmax
et du flux énergétique reçu noté Plum.
Rendement = Pmax / Plum.
6. Calculer la
puissance lumineuse reçue par le panneau dans les conditions standard
de tests.
Pmax / rendement = 530 /0,2051 =2,58 kW.
7. Après avoir
rappelé la relation entre l’éclairement énergétique noté E et le flux
énergétique noté Plum, calculer l’aire du panneau ayant
servi à obtenir les caractéristiques des conditions standard de tests.
E x aire = Plum ; aire = 2,58 103 / 1000 = 2,58 m2.
Étude expérimentale d’un
panneau photovoltaïque.
Données :
dimensions de la cellule rectangulaire : 9,5 cm x 4,8 cm.
On réalise le montage suivant afin de faire fonctionner le panneau
photovoltaïque. L’éclairement est assuré par une lampe placée à vingt
centimètres de la cellule. L’éclairement énergétique au niveau de la
cellule est E0 = 12,5 W·m–2.
Pour différentes valeurs de résistance, on relève le couple de valeurs
(intensité I ; tension U) indiqué par les multimètres.
À partir des mesures effectuées, on obtient la courbe de puissance du
panneau photovoltaïque, fournie ci-dessous.
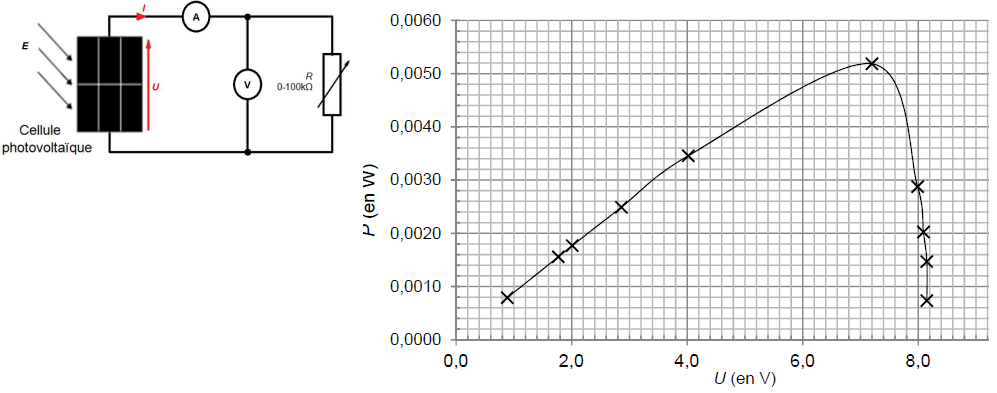
8. Déterminer les
coordonnées notées (Uopt ; Pmax) du point de
fonctionnement optimal de la cellule étudiée.
Uopt =7,4 V ; Pmax=0,0052 W
9. Montrer que le
flux énergétique reçu par la cellule dans les conditions de
l’expérience,noté Plum, vaut environ 0,057 W.
Plum = E0 x aire =12,5 x 0,095 x0,048 = 0,057
W.
10. Déterminer la
valeur du rendement de la cellule dans les conditions de l’expérience.
Commenter la valeur obtenue.
Pmax / Plum = 0,0052 / 0,057 =0,091 ~ 9 %,
valeur très faible.
Alimentation de la
résistance électrique d’un chauffe-eau.
On relie le panneau photovoltaïque étudié à un conducteur ohmique dont
la résistance R permet de se placer au point de fonctionnement optimal
du panneau.
Le fonctionnement d’un chauffe-eau est réalisé à faible échelle au
laboratoire. Le conducteur ohmique est immergé dans 100 mL d’eau.
L’objectif est d’augmenter la température de l’eau de 5,0°C. Dans
l’hypothèse où la totalité de la chaleur dissipée par le conducteur
ohmique est récupérée par l’eau, l’énergie à fournir par le panneau est
égale à Q = 2 090 J.
11. Indiquer le nom
donné à la conversion d’énergie électrique en énergie thermique.
Effet Joule.
12. Calculer la
durée de fonctionnement du panneau photovoltaïque nécessaire pour
chauffer l’eau ; on l’exprimera en heure puis en jour. Commenter la
valeur obtenue.
Q / Pmax =2090 /0,0052 ~40 000 s ou 11 h.
Cet unique panneau n'est pas adapté pour chauffer l'eau..
|
|





