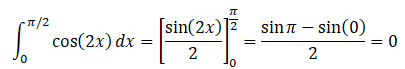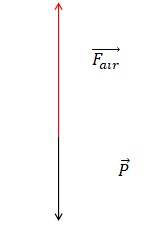Isolation
phonique, pollution atmosphérique, mouvement d'un drone, mathématiques,
bac STI2D Métropole 09 / 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Isolation phonique et
réverbération.
La réverbération est un phénomène acoustique qui désigne
la persistance d’un son dans un espace clos lorsque sa source a cessé
d’émettre. Pour atténuer ce phénomène, une solution consiste à installer des
panneaux de matériaux absorbants acoustiques sur les murs. Cet exercice
étudie les propriétés d’absorption acoustique de deux matériaux, la
mousse de mélamine et le feutre acoustique.
Donnée : On rappelle la relation entre niveau sonore et intensité
acoustique :
L = 10log(I / I0) où : - L est le niveau sonore en dB ; - I est l’intensité
acoustique du son considéré en W·m-2 ; - I0 est l’intensité acoustique
correspondant au seuil conventionnel d’audibilité, soit 10-12 W·m-2 ; -
log désigne le logarithme décimal.
Q1. Calculer la valeur de l’intensité acoustique I1 correspondant à un
son de niveau sonore L1 = 85 dB.
I1 =I0 x 10-I1 /10 =10-12 x 108,5=3,16 10-4 W m-2.
Pour caractériser l’absorption des ondes sonores dans la mousse de
mélamine, on place une source d’ondes sonores en contact avec une
plaque de ce matériau. On note I(x)
l’intensité acoustique de l’onde sonore après traversée d’une épaisseur
x de matériau absorbant.
Dans un modèle simple, on montre que l’intensité sonore I(x) dans la mousse de mélamine vérifie la relation : dI/dx=−µ I(x)
où µ est un coefficient caractéristique du matériau.
Pour la mousse de mélamine, on a :µ = 0,262 cm-1.
Pour des valeurs de x, en cm, l’intensité acoustique I(x) peut donc être obtenue en résolvant l’équation différentielle :
(E) : y ' = − 0,262 y
Q2. Déterminer les solutions sur [0 ; +∞[ de l’équation différentielle (E).
y = A exp(-0,262 x) avec A une constante.
Q3. Montrer que la fonction f définie sur [0 ; +∞[ par f(x) = 3,2.10−4exp(−0,262x) est la solution particulière de (E) vérifiant la condition initiale f(0) = 3,2.10-4.
f '(x)=-3,2 10-4 x0,262 exp(−0,262x)= -8,384 10-5 exp(−0,262x).
Repport dans (E) :
f '(x)=-3,2 10-4 x0,262 exp(−0,262x)= -0,262 x 3,2.10−4exp(−0,262x) est vérifiée qu'elle que soit x.
De plus f(0) =3,2 10-4.
Q4.
Résoudre sur [0 ; +∞[ l’équation exp(−0,262 x) = 0,5. Déterminer la
distance de propagation d au bout de laquelle l’intensité acoustique de
l’onde est divisée par 2.
-0,262 x=ln(0,5) ; x =2,65 cm.
d = 2,65 cm.
On étudie par ailleurs expérimentalement les propriétés d’une plaque
d’isolant acoustique constituée de feutrine de polyester, selon le
protocole suivant.
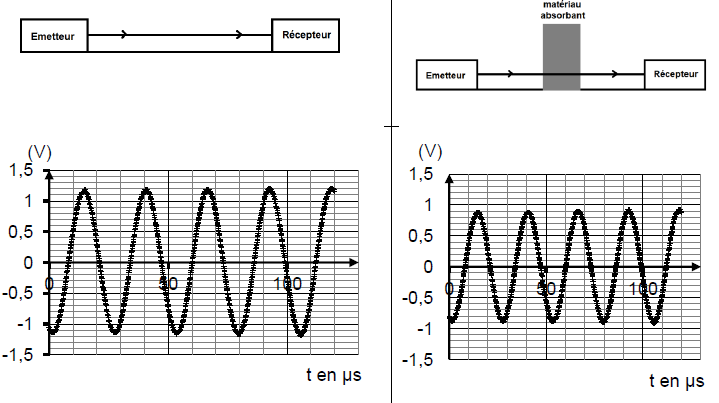
Dans une première expérience, le signal sonore est reçu directement par un récepteur après propagation dans l’air.
Dans une deuxième expérience, on intercale une plaque de feutrine de polyester entre l’émetteur et le récepteur.
Le signal reçu est, dans les deux cas, visualisé à l’oscilloscope.
La puissance de l’onde émise par l’émetteur est identique dans les
deucas. Au cours des deux expériences, on néglige l’atténuation du son
dans l’air.
On note Ua l’amplitude du signal reçu dans la première expérience, et Ub
celle du signal reçu dans la deuxième expérience, en présence de la
plaque absorbante. Les intensités acoustiques correspondantes sont
respectivement notées Ia et Ib. On précise que le rapport des intensités acoustiques est donné par la relation : Ib/Ia = (Ub/Ua)2
Q5. Calculer le rapport des amplitudes Ub/Ua .
Ua=1,2 V ; Ub =0,9 V ; Ub/Ua =0,9/1,2=0,75.
Pour une plaque d’isolant acoustique, on définit le coefficient d’absorption acoustique a= 1- Ib/Ia
, de valeur comprise entre 0 et 1, qui correspond au rapport entre
l’intensité absorbée par la plaque et l’intensité incidente. Plus le
coefficient a est élevé, plus la plaque absorbe efficacement les ondes sonores.
Q6. Montrer que la plaque étudiée est de classe D.
a =1-0,75 =0,25, valeur comprise entre 0,30 et 0,60. Donc classe D..
Impact de la pollution atmosphérique sur les bâtiments historiques
Les sculptures et monuments historiques construits en pierres calcaires
souffrent de l’action de la pollution atmosphérique des villes. Ainsi,
la dissolution du dioxyde de soufre présent dans l’air dans les eaux de
pluies entraîne la formation d’acide sulfurique H2SO4(aq) .
Celui-ci se dissocie totalement dans l’eau en libérant des ions H3O+(aq). Le pH des eaux de pluie peut alors être inférieur à 5.
Données :
• Formule du calcaire : CaCO3(s) ou (Ca2+,CO32-)(s).
• Les couples acides bases à considérer dans cette étude sont :
HCO3-(aq) / CO32-(aq)
H3O+(aq) / H2O(l)
Q1. À partir des
informations données en début d’exercice, justifier le caractère acide
des eaux de pluies dans lesquelles le dioxyde de soufre présent dans
l’air s’est dissout.
Le dioxyde de soufre se dissocie totalement dans l’eau en libérant des ions H3O+(aq).
Q2. Écrire l’équation de la réaction acide-base qui a lieu lorsque les ions oxonium H3O+(aq) réagissent avec les ions carbonate CO32-(aq) du calcaire. Les ions calcium Ca2+ sont spectateurs, ils n’interviennent pas dans le bilan de la réaction.
HCO3-(aq) +H2O(l) = CO32-(aq) +H3O+(aq).
Étude expérimentale
Pour étudier au laboratoire l’action de l’eau acidifiée par l’acide
sulfurique sur la pierre composant les immeubles on met en présence un
morceau de calcaire cylindrique calibré et une solution d’acide
sulfurique dont le pH vaut 4,5.
À l’instant initial, on plonge le morceau de calcaire dans la solution,
on déclenche le chronomètre et on mesure la diminution de la masse de
calcaire au cours du temps, au milligramme près.
temps (min)
|
0
|
30
|
60
|
90
|
150
|
210
|
270
|
495
|
1000
|
mcalcaire (g)
|
4,622
|
4,622
|
4,622
|
4,621
|
4,622
|
4,620
|
4,610
|
4,605
|
4,600
|
Q3. Calculer la concentration en ions H3O+(aq) dans la solution à l’instant initial.
[H3O+] = 10-pH = 10-4,5 =3,16 10-5 mol / L.
Q4. À l’aide des données du tableau, calculer la perte de masse de calcaire a diminué pour une durée d’expérience de 4,5 h.
4,5 h = 4,5 x60 =270 min.
4,622 -4,610 = 0,012 g.
La surface du morceau de pierre en contact avec la solution d’acide sulfurique est S = 6,7 × 10-4 m² et la masse volumique du calcaire est r = 2,500 × 106 g·m-3.
Q5. Calculer la diminution du volume de la pierre, notée DV, au bout d’une durée de présence dans la solution de 4,5 h.
DV = perte de masse (g) / r =0,012 / (2,500 106)=4,8 10-9 m3.
Q6. Sachant que la variation de volume de la pierre entraine une diminution de l’épaisseur De=DV / S, montrer que la diminution d’épaisseur de la partie de la pierre en contact avec la solution d’acide sulfurique vaut : De = 7,2 μm.
De =4,8 10-9 /(6,7 10-4) =7,2 10-6 m = 7,2 µm.
En admettant que la vitesse d’attaque du calcaire par l’acide reste
constante, calculer le temps nécessaire pour que la réaction ait enlevé
une couche de 1 mm d’épaisseur au calcaire.
7,2 10-3 mm enlevé en 4,5 h.
4,5 /(7,2 10-3) ~625 heures.
La formation de gypse
La présence de dioxyde de soufre dans l’air entraîne également la
formation de gypse (sulfate de calcium) sur les pierres calcaires. Ce
dépôt de gypse protège le calcaire de l’action des pluies acides mais
il forme des dépôts noirs sur les façades.
Q7. Expliquer en quoi la formation de gypse peut limiter l’action des pluies acides sur la pierre.
Le gypse forme une fine couche protectrice sur le calcaire.
Afin de redonner aux pierres leur couleur d’origine, on peut ôter le gypse à l’aide d’une source laser ( longueur d'onde l =1064 nm = 1,064 10-6 m). Ce laser émet des impulsions lumineuses..
Q8. Montrer que l’énergie d’un photon émis par ce laser a pour valeur E = 1,87 × 10-19 J.
On donne h = 6,63 × 10-34 J·s-1 et c = 3,00 × 108 m·s-1.
E = h c / l =6,63 10-34 x3,00 108 /(1,064 10-6)=1,87 10-19 J.
Q9. À partir de la
question précédente et des caractéristiques de la source laser
utilisée, montrer que l’énergie émise lors d’une impulsion vaut environ
7,5 × 10-5J.
4,00 1014 photons émis par impulsion : 1,87 10-19 x4,00 1014=7,5 × 10-5J.
Q10. Si le laser émet n impulsions par seconde, montrer que sa puissance moyenne P vérifie : P = n x Eimpulsion.
Energie de n impulsion = 7,5 10-5 n joule.
Durée = 1 seconce ;
Puissance (watt)= énergie(J) / durée(s) = n x Eimpulsion=300 watts.
Calculer la valeur du nombre d’impulsions par seconde.
n = 300 / (7,5 10-5) =4,0 106.
L’utilisation de ce laser nécessite le port de verres de protection par l’opérateur.
Le choix du type de verre à utiliser dépend de l’énergie émise par impulsion mais aussi de l’irradiance (en W·m-2) du faisceau laser.
Q11. En considérant uniquement l’énergie émise par une impulsion, indiquer le numéro d’échelon des verres de protection nécessaires.
7,5 10-5 J correspond à un verre de type R3.
Q12. Calculer l’irradiance moyenne pour la source laser utilisée.
Expliquer pourquoi l’opérateur doit au minimum porter des protections de type R4 lors de l’utilisation du laser.
Irradiance ( W m-2) =Puissance du laser / section du laser (m2) =300 / (1,4 10-2)=2,1 104 W m-2. ( donc protection de type R4).
|
...
|
....
|
Mathématiques. (4 points).
1. Pour tout nombre réel 𝑥>0, l’expression 3ln(2𝑥)−ln(8) est égale à :
3 ln(2x) = ln((2x)3) ;
3ln(2𝑥)−ln(8) =ln [(2x)3/8]=ln[(2x)3 / 23] =ln((x3)] = 3 ln(x).
2. Soit la fonction g définie sur R par g(x) =x2 exp(-2x). On admet que g est dérivable sur R et on note g' la fonction dérivée de g. Pour tout nombre réel x, on a :
On pose u = x2 et v = exp(-2x) ; u' = 2x ; v' = -2 exp(-2x).
g'(x)=u'v+v'u = 2x exp(-2x) -2x2 exp(-2x) = 2x (1-x) exp(-2x).
3. Le plan complexe est rapporté à un repère orthonormé (O ; u, v ). On désigne par i le nombre complexe de module 1 et d’argument p/2.
Soient les points A et B d’affixes respectives zA =2 exp(ip/2) et zB = -3½+i.
Donner la forme algébrique de zA ainsi que la forme exponentielle de zB.
zA = 2[cos p/2) + i sin (p/2) ] = 2i.
Module de zB : |zB| = (3+1)½ = 2.
zB / |zB| =-3½/ 2 +0,5 i = cos ( 5p/6) + i sin(5p/6).
zB = 2 exp ( i 5p/6).
4. Calculer :
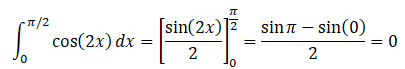
Mouvement d'un drone.
Un
drone utilisé en surveillance géographique a été filmé pendant la phase
de décollage, durant laquelle son mouvement est vertical ascendant.
Étude du mouvement du drone pendant le décollage
Q1. Déterminer le type de mouvement dont le drone est animé lors du décollage. Justifier votre réponse à l’aide de deux arguments.
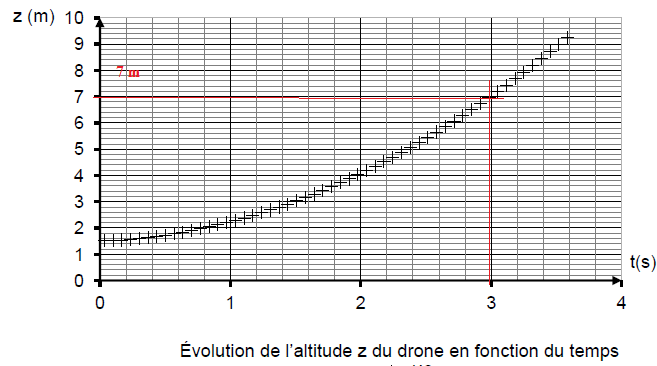

La vitesse est une fonction linéaire du temps : le mouvement est uniformément accéléré.
Altitude initiale : 0 ; vitesse initiale 0,1 m /s.
Q2. À l’aide du document 1, déterminer la distance parcourue par le drone pendant les 3 premières secondes de la phase de décollage.
7 m.
Q3. À l’aide du document 2, calculer la valeur de l’accélération az du drone pendant la phase de décollage. Préciser si cette valeur est cohérente
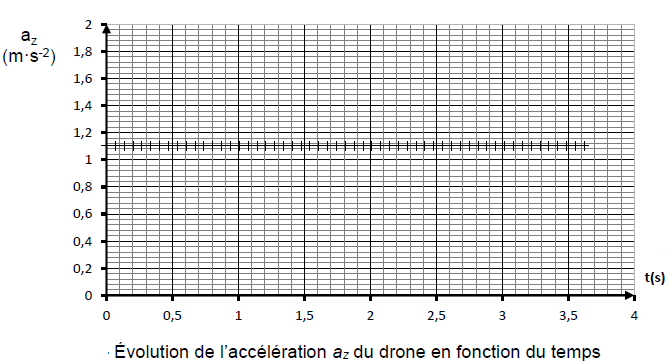
Coefficient directeur de la droite : a =3,5 / 3 ~1,2 m s-2.
Cette valeur est cohérente avec celle du document 3 : 1,1 m s-2. .
On admet que l’on peut appliquer le principe fondamental de la
dynamique dans la situation étudiée. La masse du drone étudiée est m =
895 g.
Q4. Montrer que la valeur de la résultante des forces F totale exercées sur le drone pendant ce mouvement est Ftotale =0,981 N.
Ftotale = m a =0,895 x 1,1=0,95 m s-2.
Q5. Rappeler des caractéristiques du poids P. Donner l’expression de sa valeur et la calculer.
Verticale, vers le bas, valeur mg = 0,895 x9,81 =8,78 N.
Lors du décollage, le mouvement du drone est vertical vers le haut. Il
n’est alors soumis qu’à son poids noté P et à la force, notée F air , composée de la force de traction de l’air due aux hélices et de la traînée aérodynamique.
Q6. En expliquant le raisonnement suivi, déterminer la direction, le sens et la valeur de la force F air. On s’aidera d’un schéma modélisant la situation, sans souci d’échelle.
Le mouvement étant vertical ascendant, le poids et Fair sont verticales.
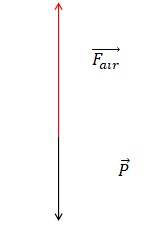
Caractéristiques de la télécommande du drone
La télécommande qui permet de piloter le drone contient quatre antennes
de longueur 3,13 cm et utilise une fréquence de l’ordre de 2,400 GHz.
Q7. Calculer la longueur d’onde du signal utilisé pour piloter le drone.
Donnée : célérité de la lumière c = 3,00 × 108 m·s-1.
l = c / fréquence=3,00 108 /(2,400 109)=0,125 m.
La longueur d’une antenne demi-onde pour une télécommande est égale à
la moitié de la longueur d’onde de la radiation transmise. Dans le cas
d’une antenne quart d’onde, cette longueur vaut le quart de la longueur
d’onde de la radiation transmise.
Q8. Déterminer si les antennes qui équipent la télécommande sont du type quart d’onde ou demi-onde.
½ l=12,5 /2 =6,25 cm.
0,25 l=12,5 /4 =3,13 cm.
Donc antennes de type quart d'onde.
|
ane.
|
|
|