Thermique,
anode sacrificielle, nombre complexe, mise au diapason d'un piano,
bac STI2D Polynésie 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1 Evolution de la
température d'un soda. .4 points.
On verse,
dans une tasse en porcelaine, du soda tout juste sorti du
réfrigérateur. La tasse est ensuite posée sur une table. La température
de l’air ambiant est supposée constante et égale à 21 °C.
On mesure la température du soda à différents instants et on trace, en
utilisant les données obtenues, le graphique ci-dessous.
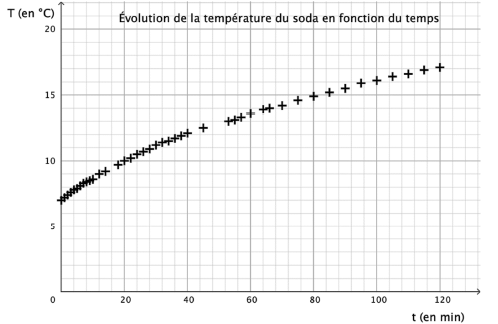
1. Rappeler les
trois modes de transfert thermique. Citer un exemple pour chacun d’eux.
Conduction dans une barre métallique chaufée à une extrémité.
Convection dans un liquide ou dans un gaz.
Rayonnement solaire.
On admet que la fonction f qui modélise l’évolution de la température
(en degré Celsius) du contenu de la tasse en fonction du temps t écoulé
(en minute) depuis la première mesure vérifie l’équation
différentielle (E) :
y'= -1/ 90 y+7 / 30.
2. Sachant que
f(0)= 7, démontrer que, pour tout réel 𝑡 positif ou nul :
f(t) =-14 exp(-t/90)+21.
Solution générale de y'+1/ 90 y=0
: y = A exp(-t/90) avec A une constante réelle.
Solution particulière de (E) : f(t) = 21.
Solution générale de (E) : y = A exp(-t/90)+21.
A l'instant initial : 7 = A+21 ; A = -14.
3. Calculer la limite de f(t) en
plus l'infini.
Le terme en exponentielle tend vers zéro ; f't) tend vers 21°C, la
température de la pièce.
4. Déterminer, à
partir de ce modèle, la valeur du temps t pour lequel la boisson
atteint la température de 20 °C. Arrondir le résultat (en minute) à
l’unité.
20=-14 exp(-t / 90) +21 ; 14 exp(-t/90) = 1 ; exp(-t/90) = 1 /14.
-t/90 = ln(1/14) ; t = 90 ln(14) ~238 minutes.
On renouvelle l’expérience en remplaçant la tasse en porcelaine par un
gobelet en acier de mêmes dimensions.
Données :
conductivité thermique de la porcelaine : 1,0 W⋅ m-1 ⋅ K-1
;
conductivité thermique de l’acier : 45,6 W⋅ m-1
⋅ K-1 .
5. Identifier,
parmi les courbes C1 et C2 figurant ci-dessous, celle qui représente
l’évolution, en fonction du temps, de la température du soda versé dans
un gobelet en acier. Expliciter le raisonnement utilisé.
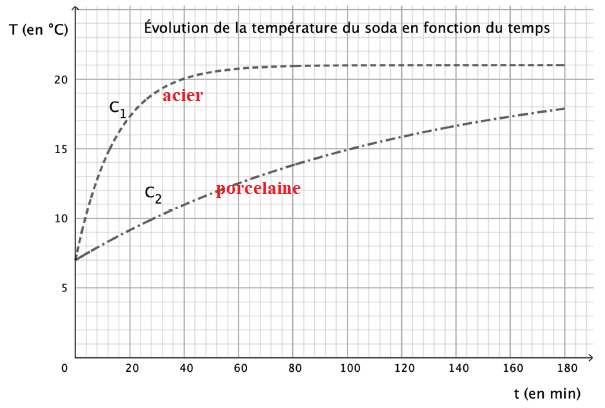
L'acier est bien meilleur conducteur que la porcelaine.
Exercice 2 (6
points).
Protection cathodique par anode sacrificielle.
La cuve interne d’un chauffe-eau est constituée d'acier. Elle est
sujette à la corrosion provoquée par l'oxydation du fer par le
dioxygène dissout dans l'eau. Il est donc nécessaire de mettre en place
des mesures de protection pour prévenir la détérioration de la cuve.
Dans le cas d’un chauffe-eau électrique, pour une utilisation optimale,
il est préconisé de changer ces anodes sacrificielles lorsqu’elles sont
consommées à 50 %. Ce qui correspond à changement tous les 5 à 10 ans.
On cherche dans la suite de cet exercice à vérifier cette durée
d’utilisation.
Étude de l’oxydation du fer.
On se propose tout d’abord d’étudier la réaction d’oxydo-réduction
entre le fer Fe et le dioxygène O2 dissout dans l’eau.
Les couples oxydant/réducteur mis en jeu sont Fe2+aq / Fe
(s) et O2aq / H2O(l).
2 fois { Fe(s) = Fe2+aq
+ 2e-}.
2H2O(l) +O2aq+4e-=4HO-aq.
1. Établir, à partir des deux
demi-équations l’équation de la réaction d’oxydation du fer par le
dioxygène.
2Fe(s) +
3H2O(l) +O2aq+4e-= 2Fe2+aq
+4HO-aq +4e-.
Simplifier : 2Fe(s) + 2H2O(l) +O2aq= 2Fe2+aq
+4HO-aq .
On dépose dans une boîte de Pétri un clou en fer que l’on recouvre
d’une solution aqueuse S saturée en chlorure de sodium contenant
quelques gouttes de phénolphtaléine, une pointe de ferricyanure de
potassium et de l’agaragar.
On précise que :
- le chlorure de sodium permet d’accélérer en laboratoire la réaction
d’oxydation ;
- l’agar-agar permet de gélifier la solution, il est neutre vis-à-vis
de toute réaction chimique ;
- la phénolphtaléine est un indicateur coloré acido-basique, qui
devient rose vifen présence d’ions hydroxydes.
- le ferricyanure de potassium est un indicateur coloré faisant
apparaître une
coloration bleue en présence d’ions fer(II).
Les résultats obtenus au bout d’une heure d’expérience apparaissent sur
la photo ci-dessous :
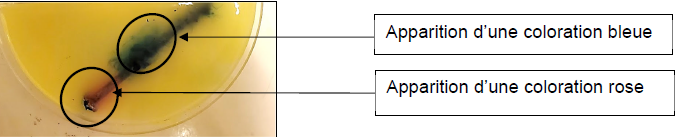
2. Identifier des
espèces chimiques formées par la réaction d’oxydation du fer réalisée
dans l’expérience décrite. Justifier.
La coloration rose met en évidence les ions hydroxydes.
La coloration bleue met en évidence les ions fer(II).
Étude de l’oxydation du
zinc.
Lorsque l’on plonge un ruban de zinc métallique dans de l’eau, le métal
zinc 𝑍𝑛(s) s’oxyde en ion Zn2+aq.
3. Indiquer, sans
calcul, comment évoluent lors de cette réaction :
-la masse de métal zinc ;
- la concentration massique des ions zinc Zn2+aq.
- la concentration massique des ions hydroxyde HO-aq.
2 fois { Zn(s) = Zn2+aq + 2e-}.
2H2O(l) +O2aq+4e-=4HO-aq.
2Zn(s) + 2H2O(l) +O2aq= 2Zne2+aq
+4HO-aq .
La masse de zinc diminue ; la
concentration massique des ions zinc Zn2+aq augmente ; la
concentration massique des ions hydroxyde HO-aq augmente..
Protection du fer par ajout de zinc.
On dispose au laboratoire de clous en fer, de rubans de zinc
métallique, de la solution S utilisée dans l’expérience ainsi que de la
verrerie de laboratoire.
Dans une solution, lorsque des ions hydroxydes HO- aq sont
en présence d’ions zinc Zn2+aq , un précipité blanc
d’hydroxyde de zinc de formule Zn(OH)2 apparaît.
4. Proposer une
expérience, en vous aidant éventuellement d’un schéma, permettant de
montrer que le zinc s’oxyde à la place du fer lorsqu’il sont reliés
électriquement.
On
dépose dans une boîte de Pétri un clou en fer entouré partiellement de
zinc que l’on recouvre d’une
solution aqueuse S saturée en chlorure de sodium contenant quelques
gouttes de phénolphtaléine, une pointe de ferricyanure de potassium et
de l’agaragar.
5. Indiquer les observations qui
permettraient de valider le rôle d’anode sacrificelle du zinc.
Apparition d'une coloration bleue sur le fer non recouvert de zinc.
Absence de la
coloration bleue sur le fer recouvert de zinc.
Le zinc s'oxyde à la place du fer.
Protection du fer par
anode sacrificielle de zinc dans le chauffe-eau.
On choisit d’installer dans le chauffe-eau une anode sacrificielle de
longueur 50 cm et de masse 1,1 kg.
La quantité Q d’électricité stockée dans cette anode de zinc vaut 9,0 x
102 Ah.
On rappelle que la quantité d’électricité stockée Q , l’intensité du
courant I en ampère qui circule dans un circuit et la durée Dt de fonctionnement du
dispositif sont liées par la relation Q = I Dt..
6. Calculer la durée de vie de l’anode en
supposant que le courant électrique entre l’anode en zinc et la cathode
en fer est constant et égal à 5,0 mA.
Quantité de matière de zinc : n = m / M(Zn) = 1,1 103 / 65,4
=16,8 mol.
Zn(s) = Zn2+aq + 2e-.
Quantité de matière d'électrons
: 2n = 33,6 mol.
Q = 2 n F = 33,6 x96500 =3,25 106 C.
Dt = Q / I = 3,25 106
/ (5 10-3) =6,5 108 s ou 1,8 105
heures ou 7,5 103 jours ou 20 ans.
7. Commenter votre résultat
vis-à-vis des préconisations du constructeur concernant la durée
d’utilisation optimale d’une anode sacrificielle.
10 ans plus tard, la masse de zinc est divisée par deux. Les
préconisations du constructeur sont correctes.
|
...
|
....
|
Exercie
3. (4 points).
Filtre et fonction de transfert
Un filtre dans un circuit électrique permet de transmettre
sélectivement certaines composantes du spectre en fréquence d’un signal.
On considère le filtre, composé d’une résistance R et d’un condensateur
C.
On appelle fonction de transfert de ce filtre, la fonction 𝐻 définie
par :
H = 1 /(1+i RCw).
où : R = 106 ohms et C = 10-6 F.
i est le nombre complexe de module 1 et d’argument p/2.
w est
la pulsation du signal aux bornes du circuit, exprimée en rad∙s-1.
La pulsation de coupure du filtre est définie par wC = 1 /(RC).
1. Calculer wC, puis montrer
que H(wC)
= 0,5-0,5 i.
wC=1
/(RC )= 1 /(106 x 10-6 )= 1.
H(wC)
=1 /(1+i)= (1-i) / (1+i)(1-i) = (1-i) / 2.
2. Écrire H(wC) sous forme
exponentielle.
Module de H(wC)
: (0,52 +0,52)½ =0,5 x2½.
H(wC) /
module de H(wC)
=1/2½ -1/2½ =cos(-p/4) + i sin(-p/4)= exp(-ip/4).
H(wC)=0,5
x2½exp(-ip/4).
La réponse en gain du circuit, notée GdB et exprimée en
décibel, vaut pour cette fréquence de coupure :
GdB= 20 log(|H(wC)|)
3. Montrer que GdB
=10 log(2).
log(|H(wC)|)
=log(0,5 x2½)= log (0,5) +½log(2) = -log(2) +½log(2) =
-½log(2).
GdB = 20 (-½log(2) = -10 log(2).
On pose en cascade un deuxième filtre identique de même pulsation de
coupure qui est tel que la fonction de transfert de ces deux filtres
est égale au produit des fonctions de transfert de chacun des deux
filtres. Ainsi :
HT(wC)
= H(wC)
x H(wC).
4. Déduire de la
question 2 le module et un argument de HT(wC).
H(wC)x
H(wC)=0,5
x2½exp(-ip/4)
x0,5 x2½exp(-ip/4)=0,25
x2 exp(-ip/2)=0,5
exp(-ip/2).
Exercice 4. 6
points.
Mise au diapason d’un piano.
Après le transport d’un piano, il convient de vérifier s’il est
nécessaire de le mettre au diapason, c’est-à-dire d’ajuster l’ensemble
des cordes pour régler sa justesse. On peut rapidement vérifier si le
piano nécessite ce 2404réglage en s’aidant d’un diapason qui émet la
note La3 dont la fréquence vaut 440 Hz.
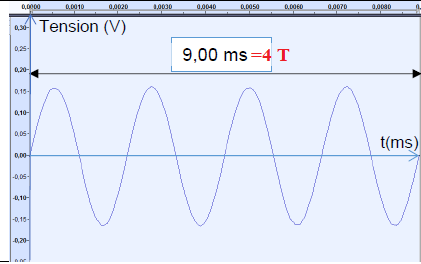
1. Déterminer la période du son émis par le diapason.
T = 9,00 / 4 =2,25 ms.
2. En déduire sa fréquence.
f = 1 /T = 1 /(2,25 10-3) =444 Hz.
On joue maintenant un La3 sur le piano.
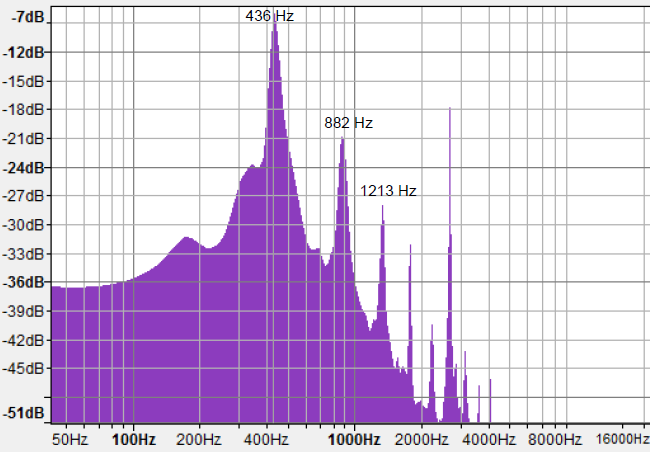
3. Donner le nom du type de graphique représenté.
Spectre en fréquences.
4. Indiquer si le son obtenu est un son pur ou complexe. Justifier.
Le son est complexe, présence de plusieurs harmoniques.
5. Retrouver la fréquence de la note jouée et discuter la nécessité d’accorder le piano ou non.
Fréquence du fondamental : 436 Hz. différent de 440 Hz et présence d'harmoniques. Il faut accorder le piano.
6. Définir les notions de timbre et de hauteur d’un son.
Hauteur : fréquence fondamentale.
Le timbre est constitué de toutes les fréquences du son sauf la fréquence du fondmental.
Insonorisation de la pièce.
Il est souvent indispensable d’isoler davantage les cloisons séparant
la pièce où se trouve le piano des pièces voisines. Une mesure du
niveau sonore maximal près du piano est réalisée.
7. Nommer l’appareil permettant de mesurer un niveau sonore.
Sonomètre.
8. Montrer que l’intensité acoustique I1 correspondant au niveau sonore L1 = 92,7 dB mesuré est égal à 1,86 x 10-3 Wꞏm - 2.
I1 = 10-12 x 109,27=10-2,73 =1,86 x 10-3 Wꞏm - 2.
Pour une meilleure isolation phonique, une nouvelle cloison va être
installée entre la salle du piano et la salle de séjour qui est la
pièce voisine.
9. Compléter le document-réponse, avec les mots incidente, réfléchie, transmise, absorbée.
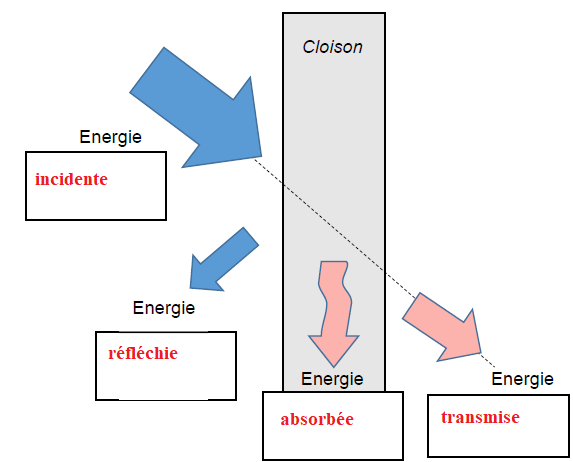
Le niveau sonore relevé à proximité de la cloison dans la pièce où l’on joue du piano est de 87 dB.
Le niveau sonore de l’autre côté de la cloison doit être conforme à celui d’une salle de séjour (40 dB).
10. Calculer l’indice d’affaiblissement acoustique R nécessaire.
R = 87-40 = 47 dB
11. Choisir le type de cloison qui vous parait le mieux adapté. Justifier.
Laine minérale 2BA13, épaisseur 12 cm ; R = 50 dB.
|
ane.
|
|
|





