Combustion de l’éthanol.
1. Écrire une
formule semi-développée de l’éthanol.
2 Entourer le
groupement caractéristique sur la formule semi-développée et nommer la
famille chimique correspondante.
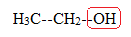alcool primaire.
Les produits de la réaction de combustion complète de l’éthanol dans le
dioxygène O2(g) de l’air sont deux gaz : le dioxyde de
carbone et la vapeur d’eau.
3. Écrire
l’équation de réaction de combustion complète de l’éthanol dans le
dioxygène de l’air.
C2H6O + 3O2 --> 2CO2 + 3H2O.
Émission de dioxyde de
carbone.
La consommation moyenne du moteur, pour cent kilomètres parcourus par
cette voiture, est de 6,1 litres d’éthanol. La combustion est
considérée comme complète.
4. Vérifier que la
masse d’éthanol consommé par le moteur est de 48 g pour un kilomètre.
Masse d'éthanol = volume (L) x masse volumique ( g
/ L ) =6,1 x 789 =4,8 10
3 g.
4,8 10
3 / 100 = 48 g / km.
La masse de CO
2 émis par le véhicule est proportionnelle à
la masse d’éthanol consommé. Cette situation est représentée ci-dessous.
5. Déterminer la
masse de dioxyde de carbone émis par le moteur fonctionnant à
l’éthanol, pour un kilomètre parcouru.
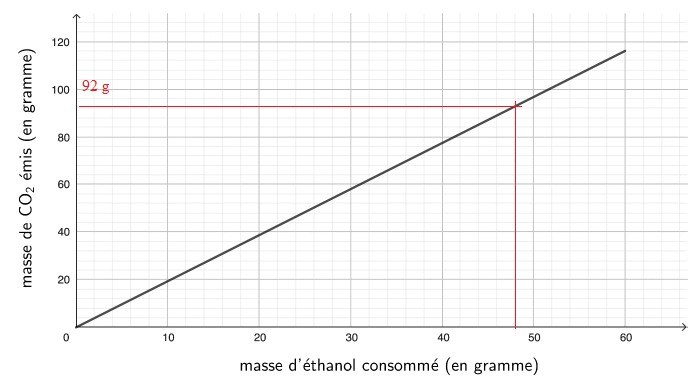
La masse de dioxyde de carbone émis par le moteur est voisine de 110 g,
pour un kilomètre parcouru, lorsque le carburant utilisé est de
l’essence sans plomb.
6. Comparer
l’émission de dioxyde de carbone selon le carburant utilisé.
L’émission de
dioxyde de carbone est inférieure d'environ 20 % dans le cas de
l'éthanol.
Montée en température du
moteur.
La température du moteur (exprimée en °C) est modélisée par une
fonction
q
dépendant du temps (exprimé en secondes) écoulé depuis le démarrage du
moteur. On admet que la fonction
q, définie et dérivable sur
[0 ;+∞[, est une solution sur cet intervalle de l’équation
différentielle suivante : y’=−1 /180 y+4 / 9.
7. Déterminer les
solutions sur [0 ; +oo[ de cette équation différentielle.
Solution générale de l'équation y' +y /180 y = 0 : y = A exp(-t /
180) avec A une constante.
Solution particulière : y = 4 x180 / 9 = 80.
Solution générale :
y
= A exp(-t / 180) +80.
À t = 0 , la température du moteur est de 20 °C.
8. Montrer alors
que la fonction
q
est définie sur [0 ; + ∞[ par :
q(t)=80 –60 exp(−
t/180).
20 = A+80 ; A = -60.
9. Résoudre sur [0
; + ∞[ l’équation
q(t)=79.
79=80–60 exp(−
t/180).
1 =60 exp(− t/180) ; ln(1/60) =-t /180 ; t = 180 ln(60)
~736 s ou environ 12 min.
Le changement de carburant ne doit pas modifier la montée en
température du moteur. La température optimale de fonctionnement du
moteur est de 79 °C. Cette température doit être atteinte en moins de
vingt minutes.
10. Indiquer si
cette condition est respectée.
Cette condition est respectée.
Douche solaire.
Les douches solaires fournissent de l’eau chauffée par les rayons du
soleil. Elles sont constituées d’un réservoir souple et d’une
douchette. Cet exercice propose d’étudier expérimentalement l’effet du
choix de la couleur noire du réservoir sur le rendement thermique de la
douche.
1. Indiquer, en
justifiant, un mode de transfert thermique mis en jeu pour chauffer
l’eau contenue dans cette douche solaire.
Transfert thermique par rayonnement.
L’expérience est réalisée successivement avec trois bouteilles de base
carrée et de dimensions identiques : une bouteille transparente non
peinte, une bouteille peinte en blanc et une bouteille peinte en noir.
Chacune est remplie d’environ un litre d’eau et elles sont exposées
successivement pendant 30 minutes à la lumière d’une lampe. La masse
d’eau est déterminée par pesée (après tarage des bouteilles) et la
température de l’eau est relevée avant et après l’exposition.
Un solarimètre mesure la puissance surfacique reçue par la surface de
la bouteille exposée au rayonnement de la lampe.
Caractéristiques techniques du solarimètr :
Unité de mesure : W⋅m
−2
Plage de mesure : jusqu’à 1999 W⋅m
−2
Précision : ± 5 % de la valeur lue.
Cette précision indiquera l’incertitude-type u(P) de la mesure.
La puissance surfacique P
S mesurée au début de l’expérience
vaut 985 W⋅m
−2.
3. Calculer
l’incertitude-type sur cette mesure.
985 x0,05 ~49
W⋅m−2.
4. Écrire le
résultat de la mesure avec son incertitude-type.
985 ±49 W m
-2.
À la fin de l’expérience, une deuxième mesure de la puissance
surfacique donne 992 W⋅m
−2.
5. Justifier qu’on
peut considérer que la puissance surfacique est la même pour ces deux
mesures.
992 appartient à l'intervalle [985-49 ; 985 + 49].
Résultats expérimentaux.
La surface de la bouteille exposée à la lumière est assimilée à un
rectangle de largeur 6,5 cm et de longueur 21,0 cm.
Bouteille blanche : masse d'eau : 999 g température initiale 17,3°C,
température finale : 20 °C. Rendement 47%.
Bouteille noire : masse d'eau : 999,7 g
température initiale 16,8°C, température finale : 21,7 °C.
Bouteille non peinte :
masse d'eau : 998,4 g température initiale 17,5°C, température finale :
21,1 °C. Rendement 60%.
6.
Indiquer le rôle de la bouteille non peinte.
Elle joue le rôle de référence, de témoin.
7. Interpréter la différence de
rendement thermique entre la bouteille blanche et la bouteille non
peinte.
La bouteille blanche réfléchit davantage le rayonnement solaire reçu.
Dans la suite de l’exercice, on prend pour valeur de la puissance
surfacique : PS = 985 W⋅m−2.
8. Montrer que,
pour la durée d’exposition de 30 minutes, l’énergie lumineuse E reçue
par chaque bouteille est égale à 24 kJ.
Aire d'une bouteille :6,5 x21 =136,5 cm2 = 0,01365 m2.
985 x 0,01365 = 13,44 W.
Energie reçue : 13,44 x30 x60 =2,4 104 J = 24 kJ.
9. Calculer le
transfert thermique Q reçu par l’eau dans la bouteille noire pendant
son élévation de température.
Donnée : capacité massique thermique de l’eau C = 4180 J⋅kg−1⋅°C−1.
Q = m C DT =0,997
x4180 x(21,7-16,8)=2,04 104 J ~ 20 kJ.
10. Donner la
formule littérale du rendement thermique pour la bouteille noire et
montrer qu’il est voisin de 85 %.
Rendement = Q / énergie reçue = 20 / 24 =0,83 ( 83 %).
11. Conclure sur
l’intérêt de choisir des réservoirs noirs.
Les réservoirs noirs absorbent le maximum d'énergie solaire.
