Stabilité
d'un antibiotique,
pile à combustible, bac STL Polynésie 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
. |
..
..
......
...
|
Dégradation de
l'amoxicilline seule en solution aqueuse.
La dégradation de
l'amoxicilline est étudiée au laboratoire, à 30 °C et à un pH valant
3,5.
La valeur de la concentration initiale en amoxicilline vaut C0
= 1 600 µg·mL-1.
La concentration de l'amoxicilline à l'instant t, notée CAmox(t),
est évaluée toutes les
vingt-quatre heures.
1) Donner la
définition de la vitesse de disparition de l'amoxicilline, notée vd
Amox·.
vd Amox = -d CAmox(t) / dt.
On fait l'hypothèse que la dégradation de l'amoxicilline suit une loi
cinétique d'ordre 1.
2) Établir
l'équation différentielle du premier ordre vérifiée par la fonction CAmox(t).
On
notera kAmox la constante de vitesse.
-d CAmox(t) / dt = kAmox CAmox(t).
Pour une loi
cinétique d'ordre 1, les solutions générales C(t) de l'équation
différentielle
vérifient l'égalité ln (C(t) / C0) = -kt pour une certaine
valeur de k.
Dans les conditions opératoires données, on obtient les résultats
expérimentaux
suivants:
| t(h) |
0
|
24
|
18
|
72
|
96
|
ln (C(t) / C0)
|
0
|
-0,18
|
-0,35
|
-0,52
|
-0,70
|
Le graphique suivant
représente le nuage de points expérimentaux et la modélisation
associée:

3) Justifier que
les résultats obtenus confirment l'hypothèse d'une loi cinétique
d'ordre 1.
Les points expérimentaux coîncident avec la modélisation.
L'ajustement linéaire des points du relevé précédent permet d'obtenir
une droite passant
par les points 0(0 ; 0) et A(96 ; - 0,70).
4) Déterminer
une valeur arrondie à 10-4 du coefficient directeur de la
droite (OA).
En utilisant cette valeur arrondie, en déduire que la droite (OA) a
pour équation :
y = -0,0073t.
-0,70 / 96 = -7,3 10-3 h-1.
La droite OA passant par l'origine, son équation est y = -0,0073 t.
5)
L'ajustement précédent nous permet d'écrire ln (cAm (t)) =
-0,0073t, pour tout
t appartenant à [O ; +00 [.
a) En déduire que CAmox(t)
= 1 600 x exp(-0,0073 t) pour tout t appartenant à [O ; 00 ].
ln (C(t) / C0)= -0,0073 t ; C(t) / C0
= exp(-0,0073 t ) ; C(t) = 1600 exp(-0,0073 t).
b) Déterminer
la limite de la fonction CAmox en+o o.
Le terme en exponentielle tend vers zéro ; CAmox tend vers
zéro.
c) Dresser le
tableau de variation de CAmox.
La dérivée -1600
x0,0073 exp(-0,0073t) étant négative, la fonction est strictement
décroissante de 1600 à 0.
Dégradation de l'ion clavulanate seul en solution
aqueuse.
Pour l'acide
clavulanique (pKa = 2,7), le suivi temporel de la concentration CClav(t)
au cours du
temps est réalisé dans les mêmes conditions opératoires que
précédemment.
6) Justifier que dans ces
conditions opératoires, l'espèce prédominante est l'ion
clavulanate.
A pH = 3,5 supérieur à pKa, la forme ion clavulanate prédomine.
La seconde expérience conduit aux observations suivantes :
- valeur de la concentration initiale en ion clavulanate : C' 0
= 320 mol· L-1
;
- valeur de la constante de vitesse de la réaction : kClav=
0, 19 h-1.
Les résultats expérimentaux, traités avec la même méthode d'ajustement,
permettent
d'établir la relation ln (CClav(t) / 320) = -0,19t.
7) Comparer le
coefficient directeur de la droite (OA) à celui de la droite d'équation
:
y= -0,19t.
0,19 / 0,0073 =137.
8) Conclure en comparant
la cinétique de dégradation de l'ion clavulanate seul à celle
de l'amoxicilline seule.
L'ion clavulanate seul se dégrade beaucoup plus rapidement que
l'amoxicilline seule.
|
...
|
....
|
La pile à combustible à membrane échangeuse
de protons (PEMFC).
C'est un empilement
de cellules élémentaires identiques, constituées chacune de deux
électrodes séparées
par un électrolyte.
L'électrolyte est une membrane polymère conductrice d'ions hydrogène
(ou protons) H+ :
les ions H+ peuvent migrer à travers l'électrolyte d'une
électrode à l'autre ;
les électrons sont bloqués par cette membrane.
Le fonctionnement de chaque cellule élémentaire repose sur le principe
d'une réaction
d'oxyde-réduction se réalisant aux deux électrodes, en utilisant du
dihydrogène H2 et du
dioxygène 02 comme réactifs.
L'objectif de cet exercice est d'étudier certaines caractéristiques
physico-chimiques d'une
pile PEMFC.
1. Compléter le schéma de conversion énergétique d'une pile à combustible PEMFC.
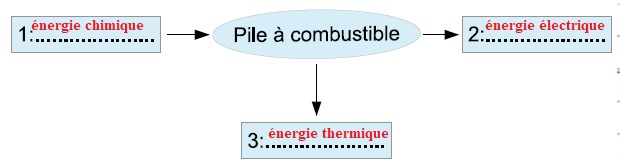
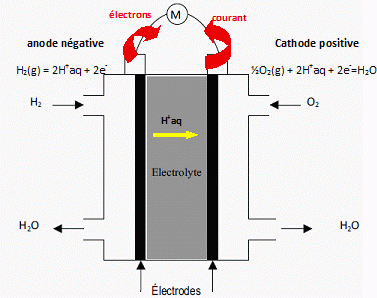
2. Compléter le schéma de la pile PEMFC lorsqu'elle est en fonctionnement pour alimenter un récepteur
électrique en indiquant :
la polarité de chaque électrode ;
le sens conventionnel de circulation du courant électrique à l'extérieur de la pile ;
le sens de déplacement des ions H+ à travers l'électrolyte.
3. Déterminer les valeurs du nombre d'oxydation de l'élément oxygène dans les espèces
chimiques du couple 02(g)/H20(l).
Dans O2(g), le nombre d'oxydation de l'élément oxygène est zéro.
Dans H2O, le nombre d'oxydation de l'élément oxygène est -II.
4. Lorsque la pile fonctionne, écrire les deux équations de demi-réaction se déroulant à
chacune des deux électrodes 1 et 2. Identifier l'anode et la cathode.
Réduction à la cathode positive : O2(g) + 4e- +4H+aq --> 2H2O(l).
Oxydation à l'anode négative : 2H2(g) --> 4e- +4H+aq
5. Écrire l'équation de la réaction chimique modélisant le fonctionnement de la pile.
O2(g) + 2H2(g) --> 2H2O(l)
Les caractéristiques électriques d'une pile à combustible sont déterminées par le nombre
de cellules élémentaires montées électriquement en série et la taille de la surface active
des membranes. La pile étudiée ici est constituée de 100 cellules élémentaires en série.
On donne ci-dessous, la caractéristique électrique d'une cellule élémentaire de la pile.
Il s'agit du tracé de la tension électrique de la cellule Ucellule , exprimée en volt, en fonction de l'intensité du courant I, exprimée en ampère.
Le graphique représente le nuage de points expérimentaux « Exp » et une modélisation notée « Sim ».

6. Commenter la qualité de la modélisation du nuage de points expérimentaux.
Les points expérimentaux coïncident avec la modélisation exceptés les 3 derniers. La modélisation est de bonne qualité.
Le fonctionnement de la cellule est optimal pour la valeur I = 2,0x102 A.
7. Déterminer
graphiquement la valeur de la tension électrique aux bornes de la
cellule lors de son fonctionnement optimal. En déduire la valeur
de la tension notée Upile, aux bornes de l'association de l'ensemble des cellules constituant la pile étudiée.
Aux bornes des piles en série, les tensions s'ajoutent : Upile = 100 Ucellule = 78 V.
8. En utilisant la
réponse à la question 4. et les données fournies, déterminer la valeur
de la masse d'eau produite par une cellule élémentaire de la pile PEMC
quand elle fonctionne normalement pendant une durée Dt = 1,0 h. On suppose que pendant Dt le courant électrique circulant dans une cellule a une valeur constante.
Q = I Dt =200 x3600 =7,2 105 C.
Quantité de matière d'électrons : n(e-) = Q / F =7,2 105 / 96500 =7,46 mol.
O2(g) + 4e- +4H+aq --> 2H2O(l).
Quantité de matière d'eau : ½n(e-) =3,73 moles.
Masse d'eau : ½n(e-) M(H2O) = 3,73 x18 ~ 67 g.
|
ane.
|
|
|