Analyse
de l'eau de mer, bathymétrie, vie à bord d'un bateau, bac
Spcl Nlle Calédonie 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Analyse de l'eau de mer.
1. Données :
Masse molaire des ions chlorure : M(Cl‒) = 35,5 gꞏmol‒1
À 25°C :
- Constante d’équilibre de solubilité du chlorure d’argent Ks1(AgCl(s))= 1,8 ⨯10–10 ;
- Constante d’équilibre de solubilité du chromate d’argent Ks2(Ag2CrO4 (s)= 1,6⨯10–12.
Le pH de l’eau de mer étudiée a une valeur égale à 7,2 et sa masse volumique r vaut 1 025 kgꞏm‒3.
Définitions : chlorinité et salinité d’une eau de mer
Une eau de mer est une solution aqueuse dans laquelle sont dissous de
nombreux ions (chlorure, sodium, sulfate, magnésium…). La salinité S de
l’eau de mer correspond à la masse totale de sels dissous par
kilogramme d’eau de mer. Elle est calculée à partir de la mesure de la
chlorinité Ch grâce à la relation suivante :
S = 1,80655 ⨯ Ch
La chlorinité Ch correspond à la masse d’ions chlorure par kilogramme
d’eau de mer. Elle peut être déterminée par titrage des ions chlorure
par les ions argent Ag+.
Après avoir prélevé un échantillon de l’eau de mer à étudier, les
scientifiques cherchent à déterminer la concentration en ions chlorure
Cl‒ de celle-ci.
Compte tenu de la forte valeur de la concentration en ions, une
dilution de l'eau de mer au 1/10ème est réalisée pour effectuer le
titrage avec une solution de nitrate d'argent. L’eau de mer correspond
à la solution S0. La solution diluée correspond à la solution S1.
Q1- Déterminer la valeur du volume de solution S0 qui doit être prélevé pour préparer 100 mL de solution S1 diluée.
Dilution au dixième : il faut préler 100 / 10 = 10 mL de S0.
Q2- Donner le protocole expérimental permettant de préparer 100 mL de solution S1 à partir de la solution S0. Nommer la verrerie nécessaire à cette préparation.
Prélever 10 mL de la solution S0 à l'aide d'une pipette
jaugée et verser dans une fiole jaugée de 100 mL contenant 1/3 d'eau
distillée. Agiter. Compléter jusqu'au trait de jauge à l'aide d'eau
distillée ; agiter pour rendre homogène.
Dosage des ions chlorure par la méthode de Mohr et ses limites.
Il consiste en un titrage colorimétrique des ions chlorure présents
dans une solution à l’aide d’une solution de nitrate d’argent.
L’équation support de la réaction de titrage est :
Ag+(aq) + Cl–(aq) → AgCl(s)
L’indicateur de fin de titrage utilisé pour repérer l’équivalence est le chromate de potassium.
En effet, après l’équivalence, les ions argent versés en excès
réagissent avec les ions chromate pour former un précipité rouge de
chromate d’argent. La transformation chimique est modélisée par
l’équation :
2 Ag+(aq) + CrO42–(aq) → Ag2CrO4 (s)
Le domaine de pH pour lequel on peut utiliser la méthode de Mohr est restreint au domaine 6,5 < pH < 7,5.
Q3- Indiquer, en justifiant la réponse, si la méthode de Mohr est utilisable dans le cas présent.
Oui, le pH de l'eau de mer vaut 7,2.
Q4- Donner deux caractéristiques d’une réaction de titrage.
Rapide et totale.
Q5- Expliquer pourquoi la méthode de Mohr ne peut pas être utilisée en milieu basique.
Une partie des ions Ag+ précipite sous forme d'un solide Ag(OH).
Q6- Écrire l’équation de la réaction modélisant la dissolution dans
l’eau du chlorure d’argent puis déterminer la valeur de la solubilité
s1 du chlorure d’argent.
Ag+aq + Cl-aq -->AgCl(s) ; Ks = s12 =1,8 10-10 ; s1 =1,3 10-5 mol / L.
Q7- Écrire
l’équation de la réaction modélisant la dissolution dans l’eau du
chromate d’argent puis montrer que sa solubilité a une valeur s2 =
7,4⨯10‒5 molꞏL–1.
K2CrO4 (s)--> 2 K+ +CrO42-aq.
s2 = [CrO42-aq] ; [K+] = 2s2 ; Ks = [CrO42-aq][K+aq]2=4s23=1,6 10-12 ;
s2= 7,4 10-5 mol / L.
On admet que le précipité qui se forme en premier est le précipité de chlorure d’argent.
Q8- Expliquer qualitativement pourquoi le chromate de potassium sert d’indicateur de fin de réaction.
Tant qu'il y a des ions chlorure, les ions argent ajoutés réagissent avec les ions chlorure.
Protocole de titrage
- Verser, à l'aide d’une pipette jaugée, un volume V1 = 10,0 mL de
solution S1 d’eau de mer diluée dans un bécher puis ajouter quelques
gouttes de solution de chromate de potassium (la solution à titrer doit
devenir jaune).
- Remplir la burette graduée avec la solution titrante de nitrate d'argent de concentration C2 = 5,00 ⨯ 10‒2 molꞏL‒1 et ajuster le zéro (éliminer toute bulle d'air).
- Verser la solution titrante dans le bécher millilitre par millitre pour déterminer grossièrement le volume à l'équivalence.
- Refaire le titrage en versant rapidement la solution titrante jusqu’à
un volume inférieur à celui trouvé précédemment, puis verser la
solution goutte à goutte jusqu'à l'apparition de la couleur rouge.
- On obtient un volume à l’équivalence Veq = 11,2 mL.
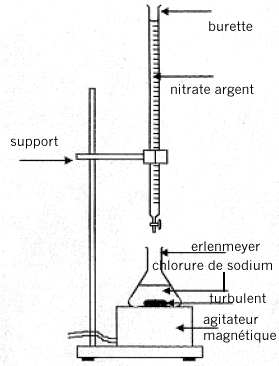
Q9- Faire un schéma
légendé du dispositif utilisé pour réaliser ce titrage, en précisant
les noms pour la verrerie et les solutions utilisées.
Q10-
Établir la relation à l’équivalence entre la concentration en ions
chlorure C1, la concentration en ions argent C2 et les volumes V1 et
Veq.
V1 C1 = C2 Véq.
Q11- Déterminer la
valeur de la concentration C1 des ions chlorure dans la solution S1
d’eau de mer diluée puis celle de la concentration des ions chlorure C0
dans l’eau de mer.
C1 = 5,00 10-2 x11,2 / 10,0 = 0,056 mol / L.
C0 = 10 C1 = 0,56 mol / L.
Q12- Montrer que la salinité S de l’eau de mer étudiée vaut 35,0 gꞏkg‒1.
0,56 x35,5 = 19,88 g / L =0,01988 kg / L.
Masse d'1 L d'eau de mer : 1,025 kg.
Ch = 0,01988 / 1,025 = 0,0194.
S = 1,80655 ⨯0,0194 = 0,035 kg / kg soit 35 gꞏkg‒1.
Bathymétrie. Le sonar émet une onde acoustique de fréquence réglable sous forme d’impulsions. Cette onde se propage vers le bas,
à la verticale du bateau. Après réflexion sur le fond marin, elle est de nouveau captée par le sonar qui mesure le décalage
temporel Dt entre l’émission et la réception du signal. Il est ensuite possible de déterminer la profondeur d à laquelle se
trouve le fond marin connaissant la célérité de l’onde dans l’eau.
Q13- Indiquer deux
phénomènes pouvant affaiblir l’amplitude du signal reçu. Préciser où
ces phénomènes interviennent (on pourra s’aider d’un schéma).
Lorsque l'onde acoustique rencontre le fond rugueux, une partie de
l'énergie du signal incident est dispersé générant des ondes
secondaires dans toutes les directions ( phénomène de diffusion).
Une partie de l'onde incidente est réfléchie sans déformation mais avec une perte d'amplitude.
La réverbération, ensemble des phénomènes d'échos multiples parasites.
Q14- Indiquer, en
justifiant la réponse, quelles sont les fréquences des sonars qui
appartiennent au domaine des fréquences audibles pour l’oreille humaine.
Domaine audible pour l'oreille humaine : 20 Hz ; 20 kHz.
À quel domaine spectral les autres fréquences appartiennent-elles ?
Fréquences supérieures à 20 kHz : ultrasons.
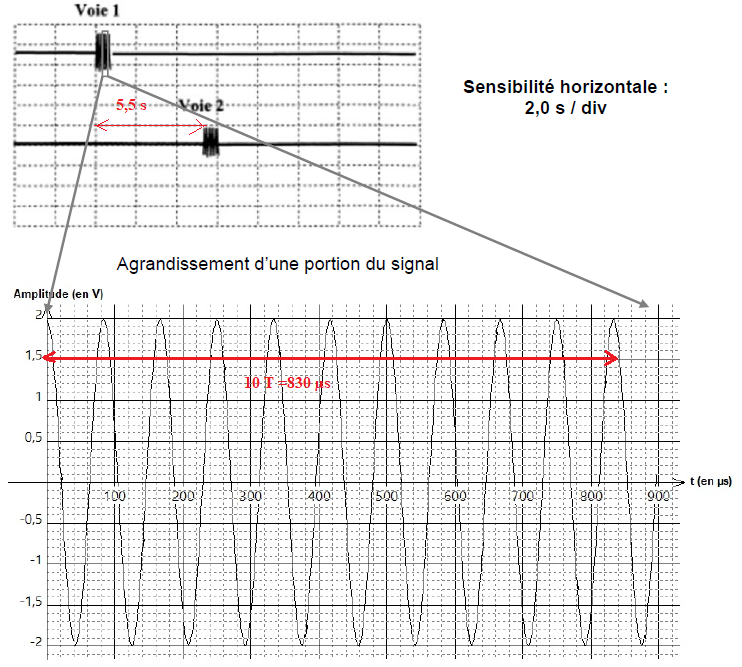
Les signaux émis et reçus par le sonar sont visualisés sur un oscilloscope. Les oscillogrammes sont donnés ci-après.
Signal émis (voie 1) et signal reçu (voie 2) par le sonar.
 Q15-
Q15- Déterminer le plus précisément possible la période T des ondes émises par le sonar.
T = 83 µs.
Q16- En déduire la fréquence f des ondes émises par le sonar.
f = 1 / T = 1 /(83 10 -6) =1,2 10 4 Hz = 12 kHz.
Q17- Indiquer si les ondes sonores sont des ondes longitudinales ou transversales.
Ce sont des ondes longitudinales.
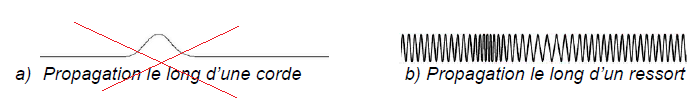
a) Propagation le long d’une corde b) Propagation le long d’un ressort
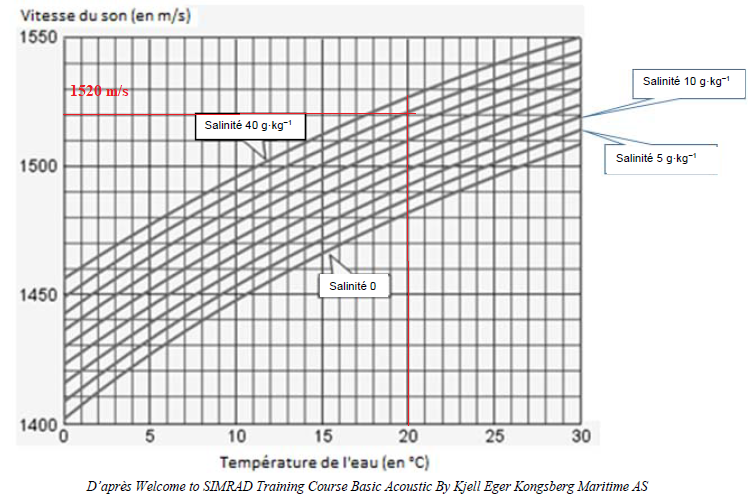
Q18- Les valeurs moyennes de température et de salinité de la mer dans la zone d’étude sont les suivantes :
température : 20 °C ; salinité : 35 gꞏkg ‒1.
Déterminer graphiquement, dans ces conditions, la valeur de la célérité v des ondes produites par le sonar dans l’eau de mer.
 Q19-
Q19- À l’aide de l’oscillogramme fourni, estimer la valeur du retard Dt entre l’émission et la réception du signal.
5,5 s.
Q20- En utilisant les résultats précédents, estimer la valeur de la distance d à laquelle se trouve le fond marin.
2d = 1520 x5,5 =8360 ; d ~4,2 km.
On suppose que u V / V= 0,005 et que l’incertitude-type sur Dt est u Dt = 0,2 s.
Q21- Déterminer la valeur de l’incertitude-type u d
u d / d = [( uV / V) 2+( uDt/ uDt ) 2] ½ =[0,005 2+(0,2 / 5,5) 2] ½=0,037.
u d = 0,037 x4,2 ~0,2 km.
Q22- Exprimer le résultat de la mesure de la distance d avec le nombre de chiffres significatifs adapté.
d =4,2 ±0,2 km.
Q23- Indiquer, en justifiant la réponse, si la fréquence utilisée est adaptée à la distance mesurée.
12 kHz est adapté pour les profondeurs allant de 3 à 12 km.
|
...
|
....
|
Impact du sonar sur la faune.
Un navire faisait des relevés topographiques à 55,0 km du lieu
d’échouage des baleines à becs. Le sonar était réglé sur une fréquence
f = 12 kHz et sa puissance était de l’ordre de 1 MW.
Les baleines à becs sont capables de percevoir les sons entre 100 Hz et
180 kHz, avec une sensibilité maximale entre 10 kHz et 100 kHz.
Dans cette plage de fréquence leur seuil d’audition est inférieur à 60 dB.
L’intensité sonore I reçue en un point M, situé à une distance R du
sonar, est liée à la puissance acoustique P du sonar par la relation :
I =P / (4pR2)
La relation entre le niveau d’intensité sonore L en dB et l’intensité sonore I en Wꞏm‒2 est la suivante :
L = 10 log ( I / I0)
Avec I0 = 7,00⨯10‒17 Wꞏm‒2 (valeur de l’intensité de référence dans l’eau pour les baleines).
Le milieu de propagation absorbe une partie de l’énergie de l’onde
sonore. Il en résulte que le niveau d’intensité sonore mesuré en un
point subit une perte A supplémentaire en décibel telle que A = aR où a
est un coefficient d’absorption qui dépend, entre autres, de la
fréquence f de l’onde, et où R est la distance entre la source et le
récepteur.
La courbe ci-dessous donne la variation du coefficient d’absorption acoustique en fonction de la fréquence.
Q24- Montrer que,
si l’on ne prend pas en compte les pertes par absorption, le niveau
d’intensité sonore à une distance de 55 km du sonar vaut environ 116 dB.
I= 106 /(4 x3,14 x(5,5 104)2)=2,6 10-5 W m-2.
L = 10 log(2,6 10-5 / 7,0 10-17) ~ 116 dB.
Q25- Estimer la
valeur de la diminution du niveau d’intensité sonore en décibel (dB)
pour le sonar utilisé par le navire et pour une distance de 55 km.
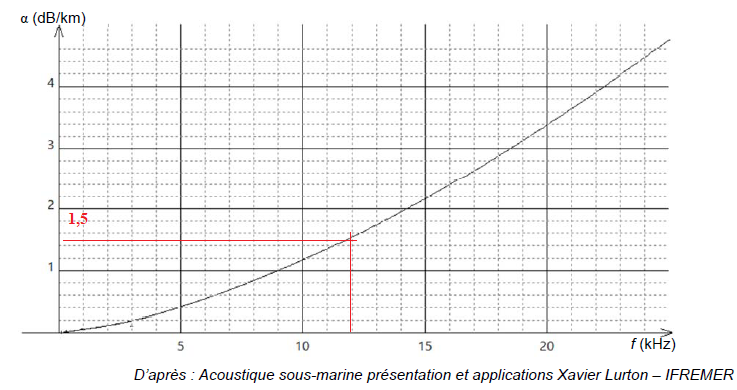
A = 1,5 x55~83 dB.
Q26- En déduire le niveau d’intensité sonore reçu par une baleine à bec située à 55 km du navire.
Indiquer, en justifiant la réponse, si les baleines à becs ont pu percevoir l’onde émise par le sonar du navire.
116-83=33 dB, valeur inférieure à 60 dB. Les baleines ne sont pas dérangées.
Le navire, d’une masse de 3 300 tonnes, accueille à son bord cinquante
personnes. Pour assurer la vie à bord, il faut avoir un stock de
nourriture mais aussi de l’eau douce. Il est impossible d’embarquer
plusieurs centaines de litres d’eau douce d’où l’obligation d’avoir un
dessalinisateur à bord afin de dessaler l’eau de mer. Les
caractéristiques du dessalinisateur utilisé sont fournies ci-après.
U = 12 V ; puissance P = 460 W ; débit : 60 L / h ; pression 50 bar ; masse à vide 56 kg ; rejet de sel 96 % minimum.
Q27- Pour une
expédition d’un mois et des besoins en eau de 20 L par personne et par
jour, déterminer le volume d’eau Veau devant être embarqué au départ
s’il n’y avait pas de moyen de production d’eau douce.
20 x30x50 =3,0 104 L.
Q28- Calculer la masse d’eau correspondante. Commenter ce résultat.
3,0 104 kgou 30 tonnes, valeur très élevée par rapport à la masse du bateau.
Q29- Déterminer la durée de fonctionnement Dt
du dessalinisateur nécessaire pour produire le volume minimum d’eau
douce nécessaire à la vie sur le bateau pendant la durée de
l’expédition. Comparer cette valeur à la durée de l’expédition et
commenter.
3,0 104 / 60 =500 h ou environ 21 jours.
Il doit fonctionner 2 jours sur 3.
Q30- Convertir la valeur du débit volumique donnée en L/ h en m3ꞏs‒1.
60 10-3 / 3600 =1,67 10-5 m3ꞏs‒1.
La canalisation à la sortie du dessalinisateur présente un diamètre de DA = 38 mm et se voit réduite pour n’être plus que de DB = 19 mm.
Q31- Prévoir qualitativement l’évolution de la vitesse de l’eau lorsque la canalisation change de section.
Le débit restant constant, si le diamètre diminue, la vitesse augmente.
Q32- On considère que l’eau se comporte comme un fluide incompressible. Calculer les surfaces des deux sections SA et SB respectivement associées aux diamètres DA et DB.
SA = 3,14 x 0,0382 / 4 =1,13 10-3 m2 ; SB = 3,14 x 0,0192 / 4 =2,8 10-4 m2 .
Calculer (en mꞏs‒1) la valeur de la vitesse de l’eau au niveau de la grande section (vA) et au niveau de la petite section (vB).
vA =1,67 10-5 / (1,13 10-3) =1,5 10-2 m /s.
vB =1,67 10-5 / (2,8 10-4) =6 10-2 m /s.
Q33- Vérifier la cohérence des résultats avec réponse à la question Q31.
Les résultats sont cohérents. Si la section est divisée par 4, la vitesse quadruple.
Soit deux points C et D de la canalisation supposée horizontale.
Le tuyau de section constante représente une canalisation d’une longueur de 6 m.
Deux manomètres placés en C et D indiquent les valeurs suivantes :
PC = 2,18 bar et PD = 1,73 bar.
Q34- Donner l’unité de la perte de charge JCD.
Pascal
Q35- Écrire le théorème de Bernoulli avec perte de charge entre les points C et D.
½rvC2 + PC + rgzC -(½rvD2 + PD + rgzD)=JCD.
Q36- Calculer la valeur de la perte de charge JCD entre les points C et D.
PC -PD =JCD =2,18 -1,73 =0,45 bar.
Q37- Indiquer les origines de la perte de charge. Proposer une solution pour la minimiser.
Frottement sur les parois, coudes, vannes robinet, longueur de la canalisation.
Diminuer la rugosité de la conduite, préférer les arrondis plutôt que les angles, diminuer la vitesse d'écoulement..
|
|