Mathématiques,
bac Polynésie 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1 .4 points.
Un sondage réalisé en France fournit les informations suivantes :
- 60% des plus de 15 ans ont l’intention de regarder les jeux Olympiques et Paralympiques (JOP) de Paris 2024 à la télévision;
- parmi ceux qui ont l’intention de regarder les JOP, 8 personnes sur 9 déclarent pratiquer une activité sportive régulière.
On choisit au hasard une personne de plus de 15 ans. On considère les évènements suivants :
- J : « la personne a l’intention de regarder les JOP Paris 2024 à la télévision »;
- S : « la personne choisie déclare pratiquer une activité sportive régulière ».
Dans les questions 1. et 2., les probabilités seront données sous la forme d’une fraction irréductible.
1. Démontrer que la
probabilité que la personne choisie ait l’intention de regarder les JOP
de Paris 2024 à la télévision et déclare pratiquer une activité
sportive régulière est de 8 / 15.
P(J n S)=0,6 x 8 / 9 = 6 x8 /(9 x10)=8 / 15.
On pourra s’appuyer sur un arbre pondéré.
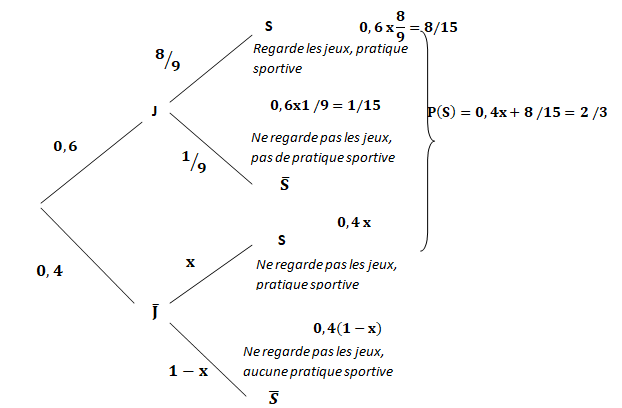
Selon ce sondage, deux personnes sur trois parmi les plus de 15 ans déclarent pratiquer une activité sportive régulière.
2. a. Calculer la
probabilité que la personne choisie n’ait pas l’intention de regarder
les JOP de Paris 2024 à la télévision et déclare pratiquer une activité
sportive régulière.
0,4x +8 /15 = 2 /3 ; 0,4 x = 10 / 15-8 / 15 = 2 /15 ;
x = (2 /15 ) / 0,4 =2 / 6 = 1 /3.
b. En déduire la probabilité de S sachant non J notée Pnon J (S).
Pnon J (S)= P(non J n S) / P(non J) = 0,4 x / 0,4 = x = 1 /3.
Dans la suite de l’exercice, les résultats seront arrondis au millième.
3. Dans le cadre d’une opération de promotion, 30 personnes de plus de 15 ans sont choisies au hasard.
On assimile ce choix à un tirage avec remise.
On note X la variable aléatoire qui donne le nombre de personnes
déclarant pratiquer une activité sportive régulière parmi les 30
personnes.
a. Déterminer la nature et les paramètres de la loi de probabilité suivie par X.
Les personnes sont choisies au hasard et pratique une activité sportive avec une probabilité de 2 /3.
X suit la loi binomiale de paramètres n = 30 et p = 2 /3.
b. Calculer la probabilité qu’exactement 16 personnes déclarent pratiquer une activité sportive régulière parmi les 30 personnes.
p(X=16) = (30 16) x (2/3)16 x(1-2 /3)30-16 =(30 16) x (2/3)16 x(1 /3)14 ~0,046.
c. La fédération
française de judo souhaite offrir une place pour la finale de l’épreuve
par équipe mixte de judo à l’Arena Champ-de-Mars pour chaque personne
déclarant pratiquer une activité sportive régulière parmi ces 30
personnes.
Le prix d’une place s’élève à 380 € et on dispose d’un budget de 10 000 euros pour cette opération.
Quelle est la probabilité que ce budget soit insuffisant ?
10 000 / 380 ~26,3 soit au maximum 26 entrées gratuites.
p(X < 26) ~0,997.
Probabilité que le budget soit insuffisant : 1-0,997 ~0,003.
Exercice 2. QCM . 5 points.
1. La solution f de l’équation différentielle y′ = −3y +7 telle que f (0) = 1 est la fonction définie sur R par :
A. f (x) = e−3x ; B. f (x) = −4/3e−3x+7/3.
C. f (x) = e−3x+7/3. D. f (x) = −10/3 e-3x-7/3.
Solution générale de y'+3y = 0 ; f(x) = A exp (3x) avec A une constante réelle.
Solution particulière y = 7 /3.
Solution générale : f(x) = A exp(-3x) + 7 /3.
f(0) = 1 = A+7 /3 ; A = -4/3.
2. La courbe d’une fonction f définie sur [0 ; +∞[ est donnée ci-dessous.
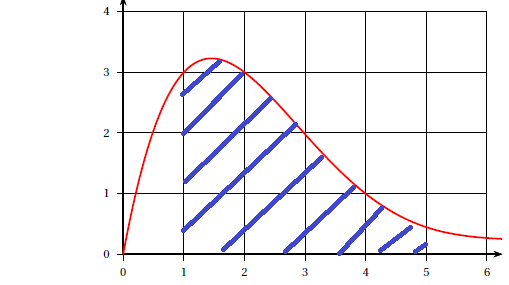
Un encadrement de l’intégrale 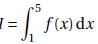 est : est :
A. 0< I <4 ; B. 1< I <5 ; C. 5< I <10 ; D. 10< I <15.
3. On considère la fonction g définie sur R par g(x) = x2 ln(x2+4).
Alors 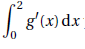 vaut, à 10−1 près : vaut, à 10−1 près :
A. 4,9 ; B. 8,3 ; C. 1,7 ; D. 7,5.
g(2) -g(0) =22ln(22+4)-0 =4 ln(8)~8,3.
4. Une professeure enseigne la spécialité mathématiques dans une classe de 31 élèves de terminale.
Elle veut former un groupe de 5 élèves. De combien de façons différentes peut-elle former un tel groupe de 5 élèves ?
A. 315 ; B. 31×30×29×28×27 ; C. 31+30+29+28+27 ; D. (31 5).
5. La professeure s’intéresse maintenant à l’autre spécialité des 31 élèves de son groupe :
- 10 élèves ont choisi la spécialité physique-chimie;
- 20 élèves ont choisi la spécialité SES;
- 1 élève a choisi la spécialité LLCE espagnol.
Elle veut former un groupe de 5 élèves comportant exactement 3 élèves
ayant choisi la spécialité SES. De combien de façons différentes
peut-elle former un tel groupe ?

Elle choisit 3 élèves parmi les 20 faisant SES : (20 3) possibilités.
Puis elle choisit 2 élèves parmi les 31-20 = 11 qui ne font pas SES.
(20 3) (11 2). Réponse A.
|
...
|
....
|
Exercie
3. (6 points).
On considère la suite (un) définie par :
u0 =8 et pour tout entier naturel n, un+1 = un −ln(un / 4).
1. a. Donner les valeurs arrondies au centième de u1 et u2.
u1 = u0-ln(u0/4)=8-ln(2)~7,30385 ~7,31.
u2 = u1-ln(u1/4)=7,31-ln(7,31 / 4)~6,70.
b. On considère la
fonction mystere définie ci-dessous en Python. On admet que, pour tout
réel strictement positif a, log(a) renvoie la valeur du logarithme
népérien de a.
def mystere(k) :
u = 8
S = 0
for i in range(k) :
S = S + u
u = u − log( u / 4 )
return S
L’exécution de mystere(10) renvoie 58.44045206721732. Que représente ce résultat ?
La somme de k premiers termes de la suite.
c. Modifier la fonction précédente afin qu’elle renvoie lamoyenne des k premiers termes de la suite (un).
Remplacer return S par return (S/k).
2. On considère la fonction f définie et dérivable sur ]0 ; +∞[ par :
f (x)= x −ln(x/4).
On donne ci-dessous une représentation graphique Cf de la fonction f pour les valeurs de x comprises entre 0 et 6.
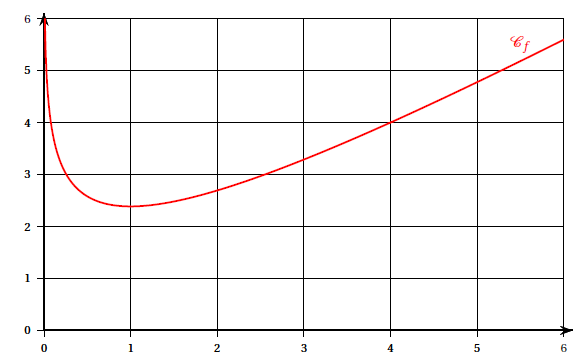
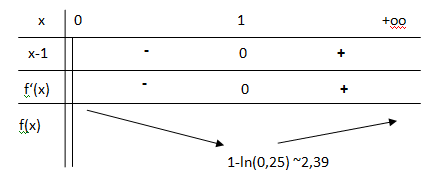
Étudier les variations de f sur ]0 ; +∞[ et dresser son tableau de variations.
On précisera la valeur exacte du minimum de f sur ]0 ; +∞[. Les limites ne sont pas demandées.
On pose u = x /4 ; u' = 1 /4 ; dérivée de ln(u) = u' / u = 1 /x.
f '(x) =1-1/x =(x-1) / x.
Dans la suite de l’exercice, on remarquera que pour tout entier naturel n, un+1 = f (un).
3. a. Démontrer, par récurrence, que pour tout entier naturel n, on a : 1<un+1 <un.
Initialisation : u0 = 8 ; u1 = 7,31. 1<u1 <u0.
La propriété est vraie au rang zéro.
Hérédité : 1<un+1 <un est supposé vraie.
La fonction f(x) étant croissante sur [1 : +oo[ : f(1) < f(un+1) <f(un ).
1-ln(0,25) <un+2 <un+1.
Or 1-ln(0,25)~2,39 , donc f(1) > 1 : 1 <un+2 <un+1.
La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout n entier naturel.
b. En déduire que la suite (un) converge vers une limite réelle.
l'encadrement précédent indique que la suite est décroissante et minorée par 1 : donc elle converge vers une limite l > 1.
On note l la valeur de cette limite
c. Résoudre l’équation f (x) = x.
x-ln(x/4) = x ; 0 = ln(x /4) ; x/4 = 1 ; x = 4.
d. En déduire la valeur de l.
La fonction est continue car dérivable :
un+1 = un-ln(un / 4) ;
à la limite : l = l-ln(l/4) soit l = 4.
Exercice 4. 5
points.
Une commune décide de remplacer le traditionnel feu d’artifice du 14 juillet par un spectacle de drones lumineux.
Pour le pilotage des drones, l’espace estmuni d’un repère orthonormé dont l’unité est la centaine demètres.
La position de chaque drone est modélisée par un point et chaque drone
est envoyé d’un point de départ D de coordonnées (2 ; 5 ; 1).
On souhaite former avec des drones des figures en les positionnant dans unmême plan P.
Trois drones sont positionnés aux points A(−1 ; −1 ; 17), B(4 ; −2 ; 4) et C(1 ; −3 ; 7).
1. Justifier que les points A, B et C ne sont pas alignés.
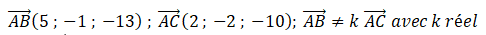
Ces deux vecteurs n'étant pas colinéaires, les points A, B, C ne sont pas alignés et ils définissent le plan (ABC).
Dans la suite, on note P le plan (ABC) et on considère le vecteur n de coordonnées (2 ; -3 ; 1)
2. a. Justifier que ce vecteur est normal au plan (ABC).
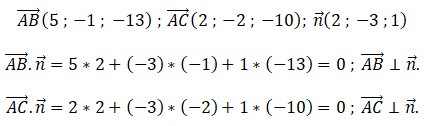
b. Démontrer qu’une équation cartésienne du plan P est 2x −3y +z −18 =0.
2x-3y+z+d = 0.
2xA-3yA+zA+d = 0 ; -2+3+17+d=0 ; d =-18.
3. Le pilote des
drones décide d’envoyer un quatrième drone en prenant comme trajectoire
la droite d dont une représentation paramétrique est donnée par :
x = 3t +2 ; y = t +5 ; z = 4t +1 avec t réel..
a. Déterminer un vecteur directeur de la droite d.
Les coefficients de t sont les coordonnées de ce vecteur directeur : (3 ; 1 ; 4).
b. Afin que ce
nouveau drone soit également placé dans le plan P, déterminer par le
calcul les coordonnées du point E, intersection de la droite d avec le
plan P.
2xE-3yE+zE-18= 0.
2(3t+2) -3(t+5)+(4t+1)-18 = 0.
7t-28=0; t = 4.
E(3*4+2 ; 4+5 ; 4*4+1) soit E( 14 ;9 ; 17).
4. Le pilote des drones décide d’envoyer un cinquième drone le long de la droite D
qui passe par le point D et qui est perpendiculaire au plan P. Ce
cinquième drone est placé lui aussi dans le plan P, soit à
l’intersection entre la droite D et le plan P. On admet que le point F(6 ; −1 ; 3) correspond à cet emplacement.
Démontrer que la distance entre le point de départ D et le plan P vaut 2*14½ centaines de mètres.
La droite (DF) étant perpendiculaire au plan (P) la distance DF est la plus petite distance du point au plan P.
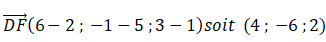
DF2 = 42 +(-6)2 +22 =56 = 14 *4 ; DF = 2*14½ .
5. L’organisatrice
du spectacle demande au pilote d’envoyer un nouveau drone dans le plan
(peu importe sa position dans le plan), toujours à partir du point D.
Sachant qu’il reste 40 secondes avant le début du spectacle et que le drone vole en trajectoire rectiligne à 18,6 m.s−1, le nouveau drone peut-il arriver à temps ?
DF = v t ; t = DF / v = 2*14½*100 /18,6 ~40,2 s.
Le drone n'arivera pas à temps.
|
ane.
|
|
|