Mathématiques,
bac Polynésie 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1 .4 points.
Les 4 affirmations se placent dans la situation suivante : A(2 ; 1 ; -1) ; B(-1 ; 2 ; 1) ; C(5 ; 0 ; -3).
On note P le plan d'équation cartésienne : x+5y-2z+3=0.
On note D la droite d'équation paramétrique:
x =-t+3 ; y =t+2 ; z = 2t+1 avec t réel.
Affirmation 1 : le vecteur n de coordonnées (1 ; 0 ; 2) est normal au plan (OAC). Faux.
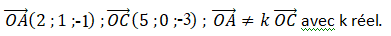
Ces deux vecteurs ne sont pas colinéaires ; les points O, A et C ne sont pas alignés ; ils définissent le plan (OAC).
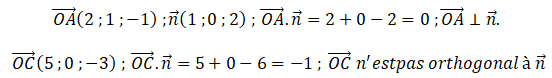
Affirmation 2 : les droites D et (AB) sont sécantes en C. Vrai.
Coordonnées du vecteur AB : -1-2 ; 2-1 ; 1-(-1) soit -3 ; 1 ; 2.
Représentation paramétrique de la droite (AB) :
x = -3 u +xA =-3u+2 ;
y = u+yA = u+1 ;
z =2u+zA = 2u-1 avec u réel.
Dans l'hypothèse où les droites D et (AB) sont sécantes :
-3u+2 = -t+3 ; t = 3u+1.
u+1 =t+2 =3u+3 ; 2u =-2 ; u = -1 ; par suite t = -2.
z =2u-1 =-3 ; z = 2t+1 = -4+1 = -3.
L'hypothèse est valide.
Coordonnées du point d'intersection : x = -t+3 = 2+3 = 5.
y = t+2 = -2+2=0 ; z =2t+1 = -4+1 =-3. Il s'agit du point C.
Affirmation 3 : la droite D est parallèle au plan P. Vrai.
Dans l'hypothèse où la droite D coupe le plan P en M(x ; y ; z) :
xM = -t+3 ; yM =t+2 ; zM =2t+1 et xM+5yM-2zM+3=0.
-t+3 +5t+10-4t-2+3 =0 t+14 ; 0t = -14.
Cette équation n'ayant pas de solution, l'hypothèse est fausse.
Le plan P et la droite (D) sont strictement parallèles.
Affirmation 4 : le plan médiateur du segment [BC), noté Q a pour équation cartésienne 3x-y-2z-7=0. Vrai.
On rappelle que le plan médiateur d’un segment est le plan perpendiculaire à ce segment et passant par son milieu.
Coordonnées du milieu I de [BC] : (-1+5) / 2 ; (2+0) / 2 ; (1-3) / 2 soit :
I(2 ; 1 ; -1).
Dans l'hypothèse où I appartient au plan Q : 3xI-yI-2zI-7 = 0 ;
6-1+2-7 = 0 est vérifié ; donc I appartient au plan Q.
Coordonnées d'un vecteur normal au plan Q : (3 ; -1 ; -2).
Coordonnées du vecteur BC : 5-(-1) ; 0-2 ; -3-1 soit 6 ; -2 ; -4.
Ces deux vecteurs étant colinéaires, le vecteur BC est normal au plan Q.
Exercice 2. 5 points.
Une
entreprise fabrique des objets en plastique en injectant dans un moule
de la matière fondue à 210 °C.On cherche à modéliser le refroidissement
du matériau à l’aide d’une fonction f donnant la température du
matériau injecté en fonction du temps t .
Le temps est exprimé en seconde et la température est exprimée en degré Celsius.
On admet que la fonction f cherchée est solution d’une équation
différentielle de la forme suivante où m est une constante réelle que
l’on cherche à déterminer :
(E) : y′ +0,02y =m.
Partie A
1. Justifier l’affichage suivant d’un logiciel de calcul formel :
Entrée : RésoudreEquationDifférentielle (y′+0,02y =m)
Sortie : → y = k ∗exp(−0.02∗t )+50∗m
Solution générale de l'équation y ' +0,02 y = 0 : y =k exp(-0,02t) avec A une constante réelle.
Solution particulière de (E) : y = m /0,02 = 50 m.
Solution générale de (E) : y = k exp(-0,02 t) +50 m.
2. La température de l’atelier est de 30 °C. On admet que la température f (t ) tend vers 30 °C lorsque t tend vers l’infini.
Démontrer que m =0,6.
Quand t tend vers +oo, le terme en exponentielle tend vers zéro et y tend vers 50 m.
50 m = 30 ; m = 3 /5 = 0,6.
3. Déterminer l’expression de la fonction f cherchée en tenant compte de la condition initiale f (0) =210.
210 = k exp(0) +30 = k +30 ; k = 180.
f(t) = 180 exp(-0,02t )+30.
Partie B
On admet ici que la température (exprimée en degré Celsius) du matériau
injecté en fonction du temps (exprimé en seconde) est donnée par la
fonction dont l’expression et une représentation graphique sont données
ci-dessous :
f (t ) =180exp(−0,02t) +30.
1. L’objet peut être démoulé lorsque sa température devient inférieure à 50°C.
a. Par lecture graphique, donner une valeur approchée du nombre T de secondes à attendre avant de démouler l’objet.
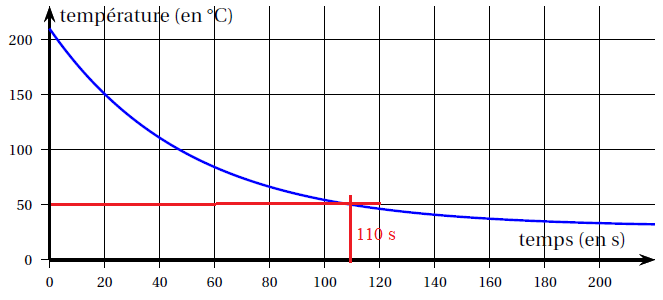
b. Déterminer par le calcul la valeur exacte de ce temps T .
180 exp(-0,02 t)+30 < 50 : 180 exp(-0,02 t) < 20.
exp(-0,02 t) <20 / 180 ; exp(-0,02t) < 1 /9.
-0,02 t < ln (1/9) ; 0,02 t > ln(9) ; t > ln(9) / 0,02 ; t > 110 s.
2. À l’aide d’une intégrale, calculer la valeur moyenne de la température sur les 100 premières secondes.
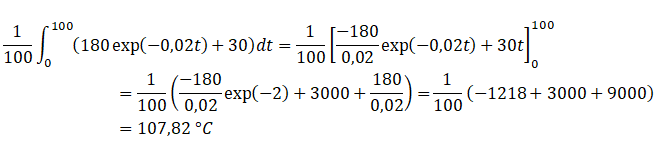
|
...
|
....
|
Exercie
3. (5 points).
Partie A
On lance trois fois de suite une pièce de monnaie bien équilibrée. On
note X la variable aléatoire qui compte le nombre de fois, sur les
trois lancers, où la pièce est retombée du côté « Face ».
1. Préciser la nature et les paramètres de la loi de probabilité suivie par X.
On répète trois fois des épreuves identiques et indépendantes. X suit une loi binomiale de paramètres n = 3 ; p = 0,5.
2. Recopier et compléter le tableau suivant donnant la loi de probabilité de X
k
|
0
|
1
|
2
|
3
|
P(X=k)
|
1 / 8
|
3 / 8
|
3 / 8
|
1 / 8
|
P(X=0) =( 30 ) x0,50x(1-0,5)3-0 =1 /8.
P(X=1) =( 31 ) x0,51x(1-0,5)3-1 =3 x0,5 x0,52=3 /8.
P(X=2) =( 32 ) x0,52x(1-0,5)3-2 =3 x0,52 x0,5=3 /8.
P(X=3) =( 33 ) x0,53x(1-0,5)3-3 =3 x0,5 x0,52=1 /8.
Partie B
Voici les règles d’un jeu où le but est d’obtenir trois pièces du côté « Face » en un ou deux essais :
- On lance trois pièces équilibrées :
- Si les trois pièces sont tombées du côté « Face », la partie est gagnée;
-Sinon, les pièces tombées du côté « Face » sont conservées et on relance celles tombées du côté « Pile ».
- La partie est gagnée si on obtient trois pièces du côté « Face », sinon elle est perdue.
On considère les évènements suivants :
- G : « la partie est gagnée ».
Et pour tout entier k compris entre 0 et 3, les évènements :
- Ak : « k pièces sont tombées du côté « Face » au premier lancer ».
1. Démontrer que PA1 (G) =0,25.
Probabilité de gagner sachant qu'une pièce est tombée du côté face au
premier lancer. C'est la probabilité qu'au second lancer les deux
pièces tombent du côté face.
Nombre de résultats équiprobables au second lancer : PP ; PF ; FP ; FF.
Nombre de résultat favorable 1 sur 4.
2. Recopier et compléter l’arbre pondéré ci-dessous :
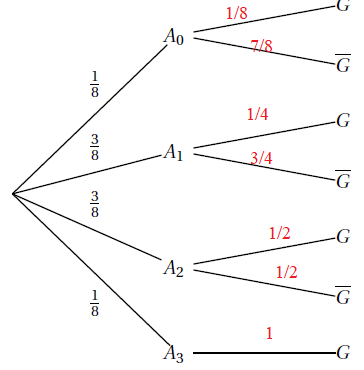
3. Démontrer que la probabilité p de gagner à ce jeu est p =27 / 64.
Loi des probabilités totales :
p = P(A0) x PA0 (G)+P(A1) x PA1 (G)+P(A2) x PA2 (G)+P(A3) x PA3 (G).
p =1 /8 x1 /8 +3 /8 x1 /4 +3 /8 x1 /2 +1 /8 x1 =(1+6+12+8) / 64 = 27 / 64.
4. La partie a été gagnée. Quelle est la probabilité qu’exactement une pièce soit tombée du côté « Face » à la première tentative ?
PG(A1) =P(A1 n G ) / P(G) = 3 /8 x 1 /4 /(27 / 64) = 3 /32 x64 /27 =2 /9.
5. Combien de fois faut-il jouer à ce jeu pour que la probabilité de gagner au moins une partie dépasse 0,95 ?
Les parties sont indépendantes et la probabilité de gain est 27 / 64.
On appelle Y la variable aléatoire comptant le nombre de parties gagnées.
Y suit la loi binomiae de paramètres n et p = 27 / 64.
P(Y=0) =(n 0) x(27 /64)0 x(1-27 /64)n=(37 /64)n.
P(Y >1) = 1-(37 /64)n > 0,95.
(37 /64)n < 0,05 ; ln((37 /64)n ) < ln(0,05).
n ln(37 / 64) < ln(0,05).
n > ln(0,05) / ln(37 /64) ~5,46.
n > 6.
Exercice 4. 6
points.
L’objectif de cet exercice est de conjecturer en partie A puis de démontrer en partie B le comportement d’une suite.
Les deux parties peuvent cependant être traitées de manière indépendante.
On considère la suite (un) définie par u0 =3 et pour tout n entier naturel :
un+1 =4 /(5−un)
.
Partie A
1. Recopier et compléter la fonction Python suivante suite(n) qui prend comme paramètre le rang n et renvoie la valeur du terme un.
def suite(n):
u =3
for i in range(n) :
u =4/(5-u)
return u
2. L’exécution de suite(2) renvoie 1.3333333333333333.
Effectuer un calcul pour vérifier et expliquer cet affichage.
u0 = 3 ; u1 =4/(5-3) =4 /2 = 2.
u2 =4 /(5-2) = 4 /3 = 1.3333333333333333.
3. À l’aide des
affichages ci-dessous, émettre une conjecture sur le sens de variation
et une conjecture sur la convergence de la suite (un).
» suite(2)
1.3333333333333333
» suite(5)
1.0058479532163742
» suite(10)
1.0000057220349845
» suite(20)
1.000000000005457
La suite est décroissante et converge vers1.
Partie B
On considère la fonction f définie et dérivable sur l’intervalle ]−oo; 5[ par :
f (x) =4/(5−x).
Ainsi, la suite (un) est définie par u0 =3 et pour tout n par un+1 = f (un).
1. Montrer que la fonction f est croissante sur l’intervalle ]−oo; 5[.
On pose u = 5-x ; u' = -1 ; f(u) =4 / u =4u-1 ; f '(u )= -4 u' u-2 ; f '(x) = 4 /(5-x)2 >0.
La dérivée étant positive, f(x) est strictement croissante.
2. Démontrer par récurrence que pour tout entier naturel n on a :
1<un+1 <un <4.
Initialisation : 1 < u1 < u0 < 4. La propriété est vraie au rang zéro.
Hérédité :
1<un+1 <un <4 est supposée vraie.
La fonction f étant strictement croissante :
f(1)< f(un+1) < f(un) <f(4).
f(1) = 1 ; f(4) = 4.
1<un+2 <un+1 <4.
La propriété est vraie au rang n+1.
Conclusion : la propriété étant vraie au rang zéro et héréditaire, elle est vraie pour tout entier naturel n.
3. a. Soit x un réel de l’intervalle ]−oo; 5[.
Prouver l’équivalence suivante : f (x) = x est équivalent à x2 −5x +4 = 0.
4 /(5-x) = x ; 4 = (5-x) x ; 4 = 5x-x2 ; x2 −5x +4 = 0.
b. Résoudre f (x) = x dans l’intervalle ]−oo; 5[.
Discriminant D = (-5)2 -4*4 = 9= 32.
Solutions : x1 =(5-3) / 2 = 1 ; x2 =(5+3) / 2 = 4.
4. Démontrer que la suite (un) est convergente.
Déterminer sa limite l.
D'après la question2 : un+1 < un : la suite est décroissante.
1 < un : la suite est minorée par 1.
La suite est décroissante et minorée par 1, donc elle converge.
f est continue car dérivable et un+1 = f(un).
l est solution de f(x)=x.
(un) est décroissante et u0 = 3 < 4 :donc l = 1.
5. Le comportement de la suite serait-il identique en choisissant comme terme initial u0 =4 au lieu de u0 =3 ?
u0 =4 ; u1 =4 /(5−4)=4.
En répétant le calcul, un = 4 quel que soit n. La suite est constante.
|
ane.
|
|
|