Evolution de la température dans une bouteille isotherme, bac Polynésie 2024.

On modélise l’évolution de la température à l’intérieur d’une bouteille isotherme en fonction du temps, sachant qu’on verse de l’eau à 92 °C dans la bouteille isotherme, puis qu’on place la bouteille dans une pièce de température constante à T_ext= 12 °C. On mesure au cours du temps avec une sonde thermométrique la température de l’eau sans ouvrir la bouteille.
1. Citer les trois modes de transfert thermique.
Conduction, convection, rayonnement.
2. Indiquer le mode du transfert thermique à travers la paroi de la bouteille et son sens.
Conduction de la boteille chaude vers la pièce, corps froid.
On suppose que l’équation différentielle suivante modélise l’évolution de la température T(t) de l’eau à l’intérieur de la bouteille isotherme en fonction du temps :
dT(t) / dt = 1 /t (T_ext-T(t)).
3. Déterminer la dimension de la constante t en la justifiant.
le terme de gauche s'exprime en K s^-1 ; celui de droite doit s'exprimer en K s^-1 ; t s'exprime en seconde.
La température de l’eau en fonction du temps, solution de cette équation différentielle, est de la forme :
T(t) = A exp(-t / t) +B avec A, B et t des constantes.
L’origine du temps t = 0 est choisie au moment où l’eau à la température T_ini = 92 °C est versée.
4. Établir les expressions de A et de B en fonction de la température initiale T_ini et de la température extérieure T_ext, puis calculer A et B.
A t =0 : T_ini = A + B ; au bout d'un temps très grand, le terme en exponentielle est nul : T_ext = B = 12.
Par suite A = T_ini-T_ext = 92-12 = 80.
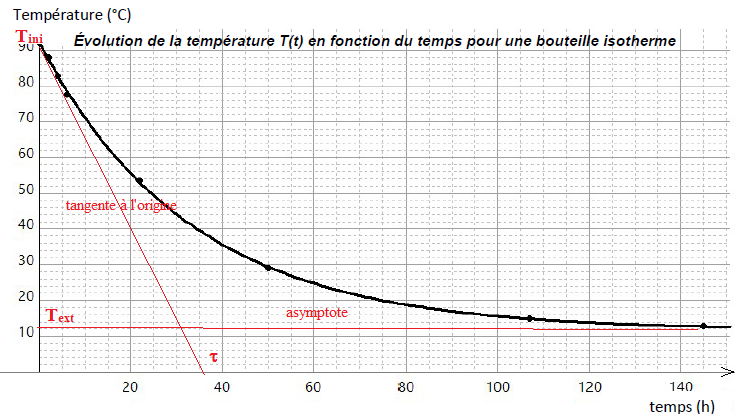
La modélisation de l’évolution de la température T(t) de l’eau en fonction du temps dans la bouteille isotherme est représentée ci-dessous.
5. Positionner T_ini, T_ext sur le graphique.
6. Montrer, par une méthode graphique, que la valeur de t est d’environ 35 heures.

7. Lors d’une randonnée en montagne, une bouteille isotherme différente est utilisée. Elle est caractérisée par une valeur de t égale à 51,2 heures. De l’eau à haute température est versée dans la bouteille le soir à 21 h. La loi T(t) = A exp(-t / t) +B
reste ici valable mais les nouvelles conditions de température donnent ici A = 78 °C et B = 10 °C. Sachant que pour
faire infuser un thé, la température de l’eau doit être supérieure à 70°C, calculer jusqu’à quelle heure le lendemain matin, il est possible de faire infuser un thé au petit déjeuner. Conclure.
78 exp(-t / 51,2) +10 > 70.
exp(-t / 51,2) >60 / 78 ; exp(-t / 51,2) >0,769.
-t /51,2 > ln(0,769) ; -t / 51,2 > -0,262 : t < 13,4 heures.
21 + 13,4 -24 =10,4 heures.
Il est possible de faire infuser un thé jusqu'à 10, 4 heures le lendemain.