Mouvement du télescope James-Webb dans un champ de gravitation, bac Polynésie 2024.

On étudie le système {télescope James-Webb}, représenté par le point J, dans le référentiel héliocentrique supposé galiléen. Il subit simultanément l’interaction gravitationnelle du Soleil et celle de la Terre. Son mouvement est considéré ici comme circulaire, comme l’est celui de la Terre.
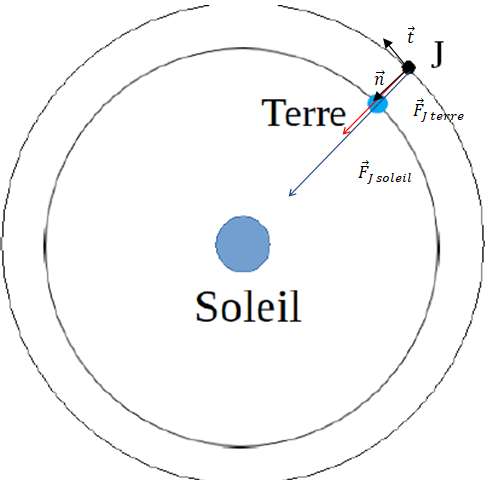
1. Positionner, sans souci d’échelle, sur le schéma, la base de Frenet au point L₂ ainsi que les forces gravitationnelles
exercées par le Soleil S sur J, et par la Terre T sur J.

2. À partir de la deuxième loi de Newton, montrer que dans l'approximation d'une trajectoire circulaire, le mouvement de J est uniforme.

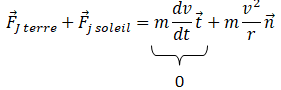
3. Donner l'expression de la valeur de la vitesse v de J dans le référentiel héliocentrique.

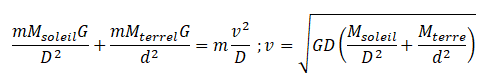
D : distance du soleil au télescope ; d : distance de la terre au télescope.
La valeur v de la vitesse du télescope est d’environ 30 km·s^-1 (proche de celle de la Terre).
4. Établir l'expression de la période de révolution T du télescope spatial James-Webb en fonction de D et v.
Le télescope décrit la circonférence 2 p D à la vitesse v durant la durée T.
2 pD = v T ; T = 2 pD / v.
5. Calculer la période de révolution T du télescope, exprimée en jours. Conclure en commentant « l’alignement » du télescope.
D =1,51 10¹¹ m.
T = 2 x 3,14 x 1,51 10¹¹ / (3,0 10⁴)=3,16 10⁷ s ou environ 366 jours ou environ une année terrestre.
Le télescope stationne bien au point L₂.