Suivi cinétique par conductimétrie de l'hydrolyse du chlorure de tertiobutyle, bac Polynésie 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Chlorure de tertiobutyle (CH3)3C-Cl noté R-Cl. masse volumique  µ = 0,850 g / mL. Equation de la réaction d'hydrolyse : RCl aq + 2H2O(l) --> ROH aq + H3O+aq + Cl-aq. Q1. Représenter la formule semi-développée de R-OH. Protocole : Verser 200 mL d'un mélange eau et de propanone dans un becher. Placer le becher dans un cristallisoir rempli d'eau. Installer la sonde du conductimètre et un dispositif d'agitation. Verser 1,0 mL de RCl et délencher l'enregistrement. Mesurer la conductivité toutes les 5 min. Q2 3. Exprimer la conductivité de la solution. s = lH3O+[H3O+] + lCl-[Cl-] . Q4. Justifier qu'il est possible de réaliser un suivi cinétique par conductimétrie de cette hydrolyse. [H3O+] =[Cl-] = C s =(lH3O++ lCl-) C. La conductivité et la concentration sont proportionnelles. Q5..Calculer la quantité de matière initiale de RCl notée n0. Masse de RCl : 0,850 g. n0 = masse  / MRCl = 0,850 /(4 *12 + 35,5 +9) = 9,2 10-3 mol. Q6 en déduire la concentration de RCl dans le mélange : C0 = n0 / Volume total = 9,2 10-3 /0,201 ~4,6 10-2 mol / L. Q7. Associer chaque courbe à RCl et à H3O+. La concentration en RCl diminue au cours du temps ( courbe 1) ; la concentration en ion H3O+ augmente au cours du temps ( courbe 2). Q8. Montrer que cette hydrolyse est totale. Courbe 1 : au bout d'un temps suffisamment long [RCl] = 0. L'hydrolyse est totale. Q9. Définir le temps de demi-réaction d'une transformation chimique. Le temps de demi-réaction t½ est la durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final. Q10. Estimer graphiquement t½. ... .... Loi de vitesse. Q11. Donner l'expression de la vitesse volumique de disparition de RCl. v =-d[RCl] / dt. Q12. Indiquer comment évolue cette vitesse au cours du temps. Cette vitesse est égale à la valeur absolue du coefficient directeur de la tangente à la courbe 1 à un temps donné. Les tangentes étant de moins en moins inclinées sur l'horizontale, cette vitesse diminue au cours du temps. Dans l'hypothèse d'une transformation d'ordre 1,  v = k [RCl] avec k une constante. 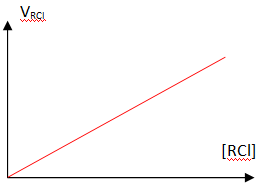Q13 Donner dans cette hypothèse l'allure de la courbe représentant la vitesse volumique de disparition de RCl en fonction de la concentration en RCl. Droite de coefficient directeur k. Q14. Etablir l'équation différentielle du premier ordre vérifiée par [RCl]. v = -d[RCl] /dt = k [RCl] ; d[RCl] /dt + k [RCl]= 0. La solution de cette équation est [RCl] = A exp(-kt). Q15. Déterminer la valeur de A. A l'instant initial [RCl] t= 0 = A =C0 = 4,6 10-2 mol / L. Q16. Calculer le coefficient directeur de la droite suivante. 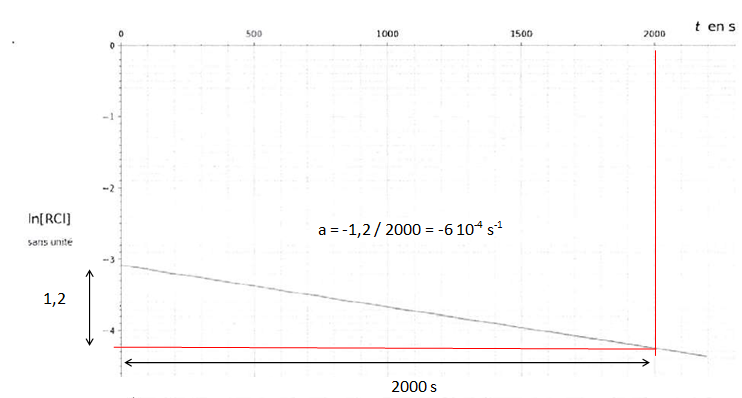On donne k = -a et t½ = ln2 / k. Q17. Calculer t½. t½ = ln 2 / (6 10-4) ~1,2 103 s en accord avec la valeur trouvée  à la question 10.. ane.

menu