Mathématiques, Bac Polynésie 09 / 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1. (5points). Une concession automobile vend deux sortes de véhicules : - 60% sont des véhicules tout-électrique; 40% sont des véhicules hybrides rechargeables. 75% des acheteurs de véhicules tout-électrique et 52% des acheteurs de véhicules hybrides ont la possibilité matérielle d’installer une borne de recharge à domicile. On choisit un acheteur au hasard et on considère les évènements suivants : - E : « l’acheteur choisit un véhicule tout-électrique »; - B : « l’acheteur a la possibilité d’installer une borne de recharge à son domicile ». Dans l’ensemble de l’exercice, les probabilités seront arrondies au millième si nécessaire. 1. Calculer la probabilité que l’acheteur choisisse un véhicule tout-électrique et qu’il ait la possibilité d’installer une borne de recharge à son domicile.  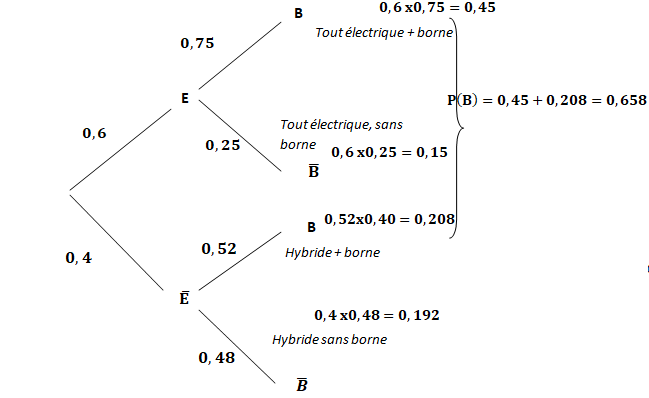p(E n B) =0,6 x0,75=0,45. 2. Démontrer que P(B) = 0,658. 3. Un acheteur a la possibilité d’installer une borne de recharge à son domicile. Quelle est la probabilité qu’il choisisse un véhicule tout-électrique ? p(B n E) / p(B) =0,45 / 0,658 =0,684. 4. On choisit un échantillon de 20 acheteurs. On assimile ce prélèvement à un tirage avec remise. On note X la variable aléatoire qui donne le nombre total d’acheteurs pouvant installer une borne de recharge à leur domicile parmi l’échantillon de 20 acheteurs. a. Déterminer la nature et les paramètres de la loi de probabilité suivie par X. C'est un schéma de bernoulli. : on répète 20 expériences aléatoires ayant deux issues, identiques et indépendantes entre elles.  X suit la loi binomiale de paramètre n = 20 et p =0,658. b. Calculer P(X = 8). P(X)=8  = (20 8) x 0,6588x(1-0,658)12=0,0113. c. Calculer la probabilité qu’au moins 10 acheteurs puissent installer une borne de recharge. p(X > 10) = 1 - P(X < 9) =1-0,0452 =0,955. d. Calculer l’espérance de X. E = n p = 20 x0,658=13,16 ~ 13. e. La directrice de la concession décide d’offrir l’installation de la borne de recharge aux acheteurs ayant la possibilité d’en installer une à leur domicile. Cette installation coûte 1 200 €. En moyenne, quelle somme doit-elle prévoir d’engager pour cette offre lors de la vente de 20 véhicules? 13 x1200 =15 600 €. Exercice 2. QCM. 6 points. 1. On considère la fonction f définie sur R par f (x) = ex +x. Affirmation A : La fonction f admet pour tableau de variations le tableau ci- dessous. Vrai. 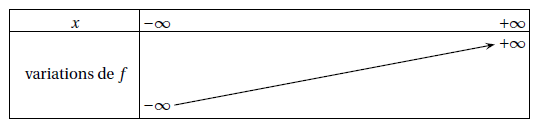En - oo: ex tend vers zéro et f(x) tend vers -oo. En +oo : ex et x tendent vers +oo. f '(x) = ex+1 >0 ; f(x) est strictement croissante. 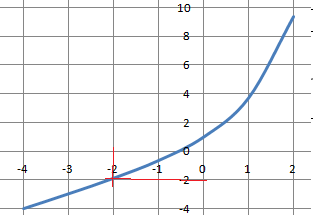Affirmation B : L’équation f (x)= −2 admet deux solutions dans R. Faux. -2 appartient à ]-oo ; +oo( et f(x) est strictement croissante sur cet intervalle. D'après le théorème de la bijection f(x) = -2 admet une seule solution. 2. Affirmation C : En +oo, la limite de (ln(x)-x2+2) / (3x2) = -1 /3. Vrai. ln(x) / (3x2) -x2 / (3x2) +2/(3x2)= ln(x) / (3x2) -1 / 3 +2/(3x2). Par croissance comparée ln(x) / (3x2) tend vers zéro ; 2/(3x2) tend vers zéro. . 3. On considère la fonction k définie et continue sur R par : k(x)= 1+2exp(−x2+1). Affirmation D : Il existe une primitive de la fonction k décroissante sur R. Faux. k(x) est strictement positive sur R. La primitive F(x) de k(x) est donc strictement croissante sur R. 4. On considère l’équation différentielle (E) : 3y′+ y = 1. Affirmation E : La fonction g définie sur R par g(x) = 4exp(−x /3)+1 est solution de l’équation différentielle (E) avec g(0) = 5. Vrai. g'(x) = -4/3 exp(-x/3) ; repport dans (E) : -4 exp(-x /3)+4exp(−x /3)+1 = 1 est vérifiée. g(0) =4 e0+1 = 5 5. Affirmation F : Une intégration par parties permet d’obtenir : On pose u = x et v ' = e-x ; u' = 1 et v = -e-x. 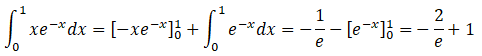Vrai. ... .... Exercice 3 (4 points). On considère une pyramide à base carrée formée de boules identiques empilées les unes sur les autres : -  le 1er étage, situé au niveau le plus haut, est composé de 1 boule; - le 2e étage, niveau juste en dessous, est composé de 4 boules; - le 3e étage possède 9 boules; - . . . - le n-ième étage possède n2 boules. Pour tout entier n > 1, on note un le nombre de boules qui composent le n-ième étage en partant du haut de la pyramide. Ainsi, un = n2. 1. Calculer le nombre total de boules d’une pyramide de 4 étages. u1 =1 ; u2 =4 ; u3 =9 ; u4 =16. Total : 30. 2. On considère la suite (Sn) définie pour tout entier n >1 par Sn = u1+u2 +. . .+un. a. Calculer S5 et interpréter ce résultat. u1 =1 ; u2 =4 ; u3 =9 ; u4 =16 ; u5 =25. S5 = 30+25 =55. Une pyramide à 5 étages compte 55 boules. b. On considère la fonction pyramide ci-dessous écrite demanière incomplète en langage Python. Recopier et compléter sur la copie le cadre ci-dessous de sorte que, pour tout entier naturel non nul n, l’instruction pyramide(n) renvoie le nombre de boules composant une pyramide de n étages. def pyramide(n) : S = 0 for i in range(1, n+1) : S = S+i^^2 return S c. Vérifier que pour tout entier naturel n : n(n +1)(2n +1) / 6+(n +1)2 =(n +1)(n +2)[2(n +1)+1] / 6. d. Démontrer par récurrence que pour tout entier n >1 : Sn =n(n +1)(2n +1) /6. Initialisation : S1 =2 x3 /6 =1. La propriété est vraie au rang 1. Hérédité : Sn =n(n +1)(2n +1) /6 est supposée vraie. Sn+1 =Sn +un+1=Sn +(n+1)2=n(n +1)(2n +1) /6 +(n+1)2=(n +1)(n +2)[2(n +1)+1] / 6. La propriété est vraie au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est donc vraie pour tout entier  n. 3. Un marchand souhaite disposer des oranges en pyramide à base carrée. Il possède 200 oranges. Combien d’oranges utilise-t-il pour construire la plus grande pyramide possible ? n(n +1)(2n +1) /6 < 200. n(n +1)(2n +1)  < 1200. 2 n3+3n2+n < 1200. Pour n = 7 : S7 =840 ; Pour n = 8 : S8 =1224. Il utilise : u1 =1 ; u2 =4 ; u3 =9 ; u4 =16 ; u5 =25 ; u6 =36 ; u7 =49. S7 =140. Exercice 4 (5 points). On considère un cube ABCDEFGH et l’espace est rapporté au repère orthonormal. Pour tout réel m appartenant à l’intervalle [0; 1], on considère les points K et L de coordonnées: K (m ; 0 ; 0) et L(1−m ; 1 ; 1). 1. Donner les coordonnées des points E et C dans ce repère. E(0 ; 0 ; 1) ; C( 1 ; 1 ; 0). 2. Dans cette question, m = 0. Ainsi, le point L(1; 1; 1) est confondu avec le point G, le point K(0; 0; 0) est confondu avec le point A et le plan (LEK) est donc le plan (GEA). a. Justifier que le vecteur suivant est normal au plan (GEA). b. Déterminer une équation cartésienne du plan (GEA). x-y+d=0. A(0 ; 0 ; 0) appartient à ce plan : x-y=0. On s’intéresse désormais à la nature de CK EL en fonction du paramètre m. 3. Dans cette question, m est un réel quelconque de l’intervalle [0; 1]. a. Démontrer que CK EL est un parallélogramme. Les côtés opposés de ce quadrilatère sont parallèles, c'est donc un parallélogramme. b. Calculer le produit scalaire suivant. c. Démontrer que CK EL est un rectangle si, et seulement si, m =0 ou m =1. Un parallélogramme possédant un angle droit est un rectangle. 4. Dans cette question, m =0,5. .Ainsi, L a pour coordonnées (0,5 ; 1 ; 1) et K a pour coordonnées (0,5 ; 0 ; 0). a. Démontrer que le parallélogramme CKEL est alors un losange. KC2 =0,52 +12 +02 =1,25 ; KE2 =0,52 +02 +12 =1,25 . KC = KE : un parallélogramme qui a deux côtés consécutifs égaux est un losange. b. À l’aide de la question 3. b., déterminer une valeur approchée au degré près de la mesure de l’angle CKE. cos (CKE) =0,25 / 1,25 = 0,2. L’angle CKE mesure environ 78°.

menu