Le
curling,
bac Métropole 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Le
curling est un sport de précision apparu au XVIe siècle en Écosse et
pratiqué sur la glace avec de lourdes pierres en granite poli. Il se
joue sur une piste de glace horizontale sur laquelle est dessinée une
cible, appelée la « maison ». Le but est de placer les pierres le plus
près possible du centre de la cible.
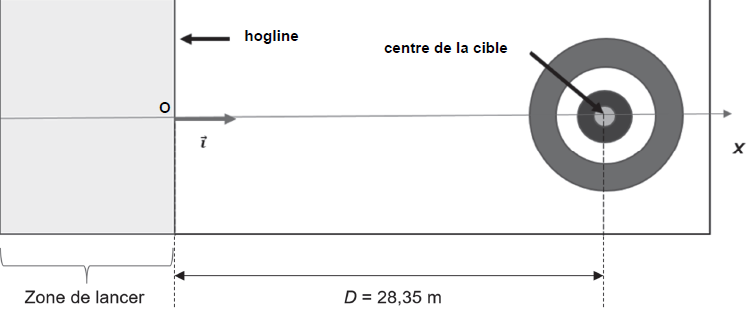
La pierre est poussée par un joueur dans la zone de lancer et doit être
lâchée avant la « hogline » (au point O) pour ne plus être touchée
ensuite, sinon elle est immédiatement retirée du jeu. Une fois la
pierre lâchée, les joueurs peuvent balayer la piste devant la
pierre ce qui a pour conséquence de réduire les frottements.
Données :
− masse d’une pierre : m = 20 kg ;
− on note µ = 0,020 le coefficient de frottement entre la glace et la pierre. La force de frottement f a pour norme f = μ∙Rn, Rn étant la norme de la réaction verticale de la piste sur la pierre
Dans tout l’exercice, on néglige les frottements de l’air et on suppose
que la trajectoire de la pierre est rectiligne suivant l’axe (Ox). La
pierre est initialement immobile. Le joueur pousse la pierre jusqu’à la
date t1 = 2,0 s en exerçant une force horizontale dans le
sens des x croissants ; la norme de cette force es supposée constante,
sa valeur est estimée à F = 35 N. Après cette phase de lancer, la
pierre est lâchée au point O de la hogline, origine du repère d’espace.
Q1. Pendant la phase de lancer, effectuer le bilan des quatre forces
appliquées au systèm {pierre}. Calculer la valeur de la norme de
chacune d’elles sachant que les deux forces verticales se compensent.
Poids, verticale vers le bas, norme P = mg = 20 x9,8 =196 N.
Action normale du support, Rn, opposée au poids.
Force de frottement f, horizontale, vers la gauche, f =0,020 x 196 =3,92 ~3,9 N.
Force exercée par le joueur, horizontale, vers la droite, F = 35 N.
Q2. Reproduire
sommairement le schéma ci-dessous de la pierre sur la piste horizontale
et y représenter ces forces sans souci d’échelle.
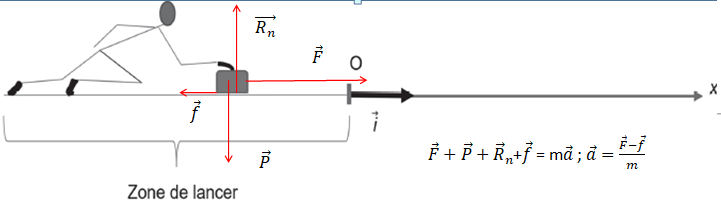
Q3. En appliquant la deuxième loi de Newton, donner que l’expression vectorielle de l’accélération de la pierre .
. En déduire la nature du mouvement de la pierre durant cette phase.
Le mouvement est uniformément accéléré.
Q4. En déduire que la valeur de la vitesse de la pierre en O est V0 = (F / m - μg) t1 et calculer sa valeur.
Selon l'axe horizontal : a = F / m - μg.
La vitesse est une primitive de l'accélération : v =(F / m - μg) t + Cste.
La vitesse initiale étant nulle : v =(F / m - μg) t .
V0 = (F / m - μg) t1 = (35 / 20 -0,02 x9,8) x2,0=3,1 m /s.
Dans les questions Q5 et Q6, on considère que les joueurs ne balaient pas la glace et que le frottement ne change pas.
Q5. En appliquant le théorème de l’énergie cinétique, établir que d = v0 2 / (2 µg) avec d, la distance par rapport à l’origine O du repère à laquelle s’immobilise la pierre. Déterminer la valeur de d.
Energie cinétique finale : 0 ; énergie cinétique initale ½mv02.
P et Rn perpendiculaire au déplacement ne travaillent pas.
Travail de f : - mµg d.
-½mv02 = -mµgd ; d = ½v02 /(µg).
d = 0,5 x3,12 /(0,02 x9,8)=24,6 m.
|
...
|
....
|
Dans
le cadre de ce modèle, on simule l'évolution de la valeur de la vitesse
v de la pierre en fonction de sa position x (sans balayage de la
piste). On obtient le graphe suivant, les mesures se faisant à
intervalles de temps constants :
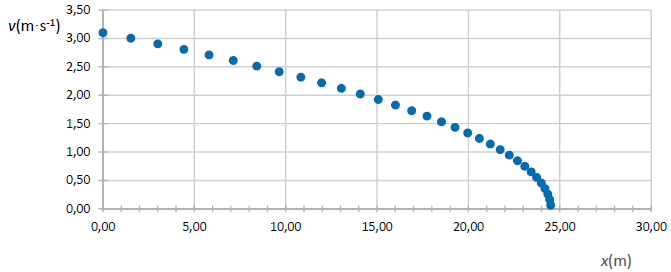
Q6. Montrer que le
résultat obtenu à la question Q5 est cohérent avec la courbe de la
figure 5. Justifier la nécessité de balayer devant la pierre.
d = 24,6 m est cohérent avec la courbe.
Sans balayage la cible ne peut pas être atteinte.
En balayant devant la pierre, les frottement diminuent et la cible peut être atteinte.
En pratique, les joueurs balaient certaines parties de la piste. Pour
rendre compte de cela, on adapte le modèle et on obtient le graphe
ci-dessous.
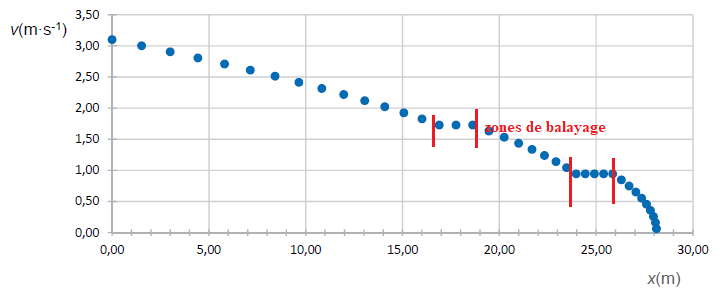
Q7. Estimer les positions des zones de la piste où les joueurs ont balayé devant la pierre.
En déduire si le balayage a ou non permis aux joueurs d’atteindre leur objectif.
Dans les zones de balayage, la vitesse reste constante : entre 17 et 19 m et entre 24 et 26 m.
La pierre parcourt 28,1 m et atteint la cible. Le balayage est donc utile.
|
ane.
|
|
|