Autour du basket-ball, bac Métropole 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Dans cet exercice on étudie trois aspects fondamentaux de ce sport : l’optimisation de la trajectoire d’un tir, le rebond du ballon lors des dribbles ainsi que la problématique des risques auditifs liés aux coups de sifflet des arbitres. Données : - masse du ballon : m = 600 g ; - rayon du ballon : Rb = 12 cm ; - valeur du champ de pesanteur supposé uniforme : g = 9,8 m·s −2 ; - rayon de l’arceau du panier : Ra = 22,5 cm ; - hauteur de l’arceau du panier, par rapport au sol : Ha = 3,05 m. 1. Étude d’une trajectoire idéale Il est légitime pour un joueur de basket-ball de se demander comment obtenir la trajectoire la plus efficace pour marquer un panier. Un site internet spécialisé dans le basket-ball donne le conseil suivant : « privilégier un angle de tir entre 47° et 55° par rapport à l’horizontale. 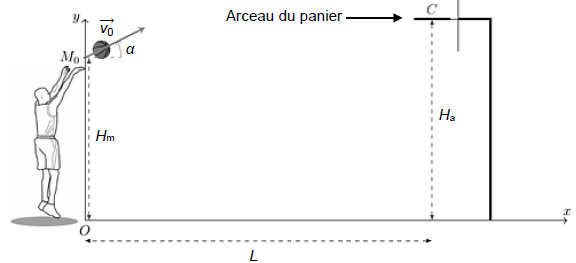On préconise les tirs en cloche de façon à avoir une exploitation maximale de la surface du panier » (source : BasketSession.com) Première modélisation Dans un premier temps, on s’intéresse au mouvement du centre de masse M d’un ballon lorsqu’un joueur réalise un lancer-franc. On réalise l’étude dans le référentiel terrestre supposé galiléen et on considère qu’une fois lancé, le ballon n’est soumis qu’à son propre poids. On néglige donc toute force de frottement de l’air sur le ballon. Quand le ballon quitte la main du joueur, son centre de masse M est situé à une hauteur Hm = 2,30 m par rapport au sol et à une distance horizontale L = 4,6 m du centre C de l’arceau du panier. On étudie le mouvement dans le repère cartésien indiqué sur la figure : le plan (Oxy) est un plan vertical contenant la main du basketteur au moment où il lâche le ballon et le centre C de l’arceau. L’instant initial est  l’instant où le ballon quitte la main, avec un vecteur vitesse initial v0 qui forme un angle a avec l’axe horizontal. L’angle a est supposé différent de 90°. Q1. Montrer que dans le plan (Oxy), les coordonnées du vecteur accélération du centre de masse M du ballon peuvent s’écrire : ax(t) = 0 ; ay(t) = -g. Le système n'étant soumis qu'à son poids, verticale, vers le bas, valeur P = mg, la seconde loi de Newton conduit à : ax(t) = 0 ; ay(t) = -g. Q2. Exprimer les coordonnées du vecteur vitesse v(t) du point M à chaque instant. La vitesse est une primitive de l'accélération et le vecteur vitesse initiale a pour coordonnées ( v0 cos a ; v0 sin a). vx(t) = v0 cos a ; vy(t) = -gt +v0 sin a. Q3. Exprimer les coordonnées du vecteur position au cours du temps. La position est une primitive de la vitesse et la position initiale a pour coordonnées ( 0 ; Hm). x(t) = v0 cos a t ; y(t) = -½gt2 +v0 sin a t +Hm. Q4. Montrer que l’équation de la trajectoire du centre de masse M du ballon peut s’écrire : t = x / ( v0 cos a) ; repport dans y : y = -½g x2 / ( v0 cos a)2 + x tan a +Hm. Un tir est considéré comme parfait lorsque le centre de masse M du ballon passe par le centre C de l’arceau du panier, le ballon ne touchant pas le bord de l’arceau. Q5. Montrer que pour un angle initial a et pour une distance L donnés, il existe une vitesse initiale v0c pour laquelle la trajectoire du centre de masse du ballon passe par le centre du panier, dont l’expression est : v0c  = [gL2 / (2 cos2 a(L tan a+Hm-Ha))]½. x=L ; y = Ha ; Ha = -½g L2 / ( v0c cos a)2 + L tan a +Hm. ½g L2 / ( v0c cos a)2 =L tan a +Hm- Ha. ( v0c cos a)2 =½g L2 / (L tan a +Hm- Ha). v0c2 = ½g L2 / [cos a2 (L tan a +Hm- Ha)]. Q6. Lors d’un lancer-franc, on montre (démonstration non demandée) qu’un tir avec un angle initial de 49,5° permet d’obtenir la vitesse initiale v0c la plus faible possible. Calculer cette vitesse. v0c  = [9,8 x4,62 / (2 cos249,5(4,6 tan 49,5+2,3-3,05))]½= 7,3 m /s. On souhaite comparer cette vitesse à celle qu’un joueur situé à une distance L = 2 m du panier doit communiquer au ballon. On trace sur les figures 2-a et 2-b la vitesse initiale à donner au ballon pour qu’il passe par le centre C de l’arceau du panier en fonction de l’angle initial a, pour la distance L = 2 m. 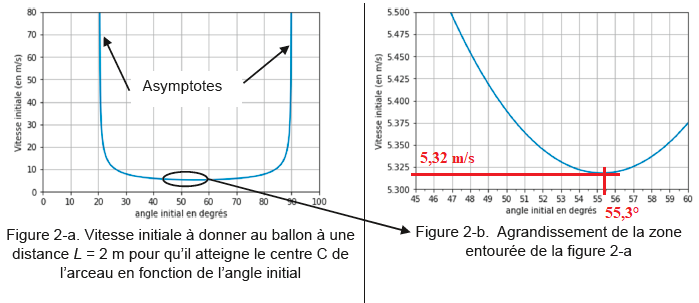Q7. Déterminer graphiquement l’angle initial à choisir pour communiquer au ballon la vitesse initiale minimale lui permettant de passer par le centre C de l’arceau, si le joueur est placé à la distance L = 2 m. Comparer les valeurs de l’angle et de la vitesse ainsi trouvées à celles obtenues pour un lancer-franc. Commenter. La vitesse initiale est plus faible que lors du lancer franc et l'angle est plus grand. le tir est plus en cloche. Q8. On distingue sur la figure 2-a deux asymptotes verticales. Expliquer pourquoi lorsque l’angle de tir initial se rapproche de 90°, la courbe de la vitesse en fonction de l’angle initial tend vers une asymptote. Lorsque l'angle se rapproche de 90° ( plus le tir se rapproche de la verticale) , v0c tend vers l'infini. On ne peut pa atteindre le panier. ... .... Deuxième modélisation Jusqu’à présent, la vitesse à communiquer au ballon a été déterminée à partir d’une seule condition : le centre de masse M du ballon doit passer par le centre C de l’arceau. Il apparaît nécessaire de prendre en compte deux conditions supplémentaires :  condition 1 : un ballon qui ne passe pas par le dessus du panier n’est pas valide ;  condition 2 : un ballon qui rebondit sur le bord du panier avant d’en atteindre le centre ne donne pas un tir parfait. On souhaite s’appuyer sur un programme rédigé en langage Python pour déterminer les trajectoires qui vérifient ces deux conditions. La figure 3 présente un extrait du code qui permet de vérifier que le ballon rentre bien dans l’arceau, dans le bon sens et sans le toucher. Le début du code (non représenté avant la ligne 80) permet de calculer la trajectoire passant par le centre C de l’arceau pour un angle initial donné, selon l’étude réalisée en première partie. Pour une trajectoire donnée, les coordonnées du centre de masse du ballon sont stockées dans les tableaux (aussi appelés listes) x et y. Les valeurs de x sont comprises entre 0 et L. Q9. Parmi les propositions ci-dessous, choisir et recopier sur la copie le code qu’il convient d’écrire pour compléter la ligne 82, afin qu’elle permette de vérifier la condition « le ballon ne passe pas au-dessus de l’arceau ». Les variables du programme, notées Ha et L, représentent respectivement les paramètres Ha et L. max(y)  < Ha : l'altitude maximale atteinte par le centre du ballon est inférieuure à l'altitude du centre du panier.  Condition " le ballon ne passe pas au-dessus de l'arceau". Les fonctions max(x) et min(x) renvoient respectivement la plus grande et la plus petite valeur du tableau x. Q10. Justifier que les lignes 89 à 92 permettent de tester la condition 2. Le ballon ne doit pas trop s'approcher de l'arceau afin de ne pas le toucher et rebondir dessus. Ligne 87 : d-bord : distance entre le centre du ballon et le bord de l'arceau. Ligne 91 :  si d_bord est inférieure au rayon du ballon la condition 2 n'est pas respectée, le ballon touche l'arceau. Q11. L’application des deux nouvelles conditions permet de déterminer que l’angle initial minimal pour réaliser un tir parfait au lancer-franc est voisin de 45°. Commenter cette valeur au regard des conseils fournis par le site internet cité en début d’exercice. L'angle de tir doit être compris entre 47° et 55°, valeur supérieure à l'angle minimal de 45° indiqué par la simulation. Ces indications sont en accord. 2. Étude du dribble et du rebond du ballon Au basket-ball, il est interdit de se déplacer en portant la balle sur plus de trois pas. Il faut donc la faire rebondir sur le sol (c’est le dribble). Il est donc important d’étudier les caractéristiques de ce rebond. À cette fin, on réalise le protocole suivant :  un ballon est lâché, sans vitesse initiale, d’une hauteur voisine d’un mètre ;  il tombe, rebondit sur le sol dur et remonte ;  le pointage du centre de masse M du ballon est réalisé à l’aide d’une chronophotographie. Ces données permettent d’obtenir les représentations graphiques de l’évolution des énergies cinétique, potentielle de pesanteur et mécanique du ballon au cours du temps. 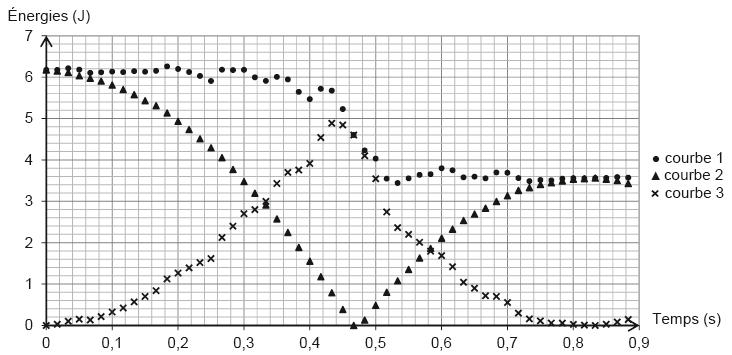Q12. Parmi les courbes 1, 2 et 3 de la figure 4, identifier celles qui représentent l’évolution de l’énergie cinétique, de l’énergie potentielle de pesanteur et de l’énergie mécanique. Justifier chacune de ces identifications. Courbe 2 : l'énergie potentielle diminue lors de la chute puis croït après le rebond. Courbe 3. l'énergie cinétique initialement nulle, augmente lors de la chute. Courbe 1 : l'énergie mécanique est la somme des énergies cinétique et potentielle de pesanteur. Q13. Montrer que l’énergie perdue par le ballon lors du rebond est voisine de 2,5 J. Avant rebond, l'énergie mécanique est voisine de 6 J. Après rebond cette énergie est voisine de 3,5 J. Perte d'énergie mécanique 6-3,5 = 2,5 J. Q14. Indiquer, en justifiant, s’il est raisonnable dans cette étude de négliger les frottements en dehors du moment où le ballon rebondit. En dehors du moment de rebond, l'énergie mécanique est à peu près constante : on peut négliger les frottements. Q15. Lorsqu’on dribble, on ne lâche pas le ballon mais on le pousse vers le bas assez fort pour qu’il remonte suffisamment haut pour continuer à dribbler. Déterminer la vitesse initiale minimale à communiquer à un ballon lancé d’une hauteur d’un mètre pour qu’il remonte au moins à cette même hauteur. On admet que la perte énergétique lors du rebond est la même qu’à la question Q13. Position 1 : altitude h = 1,0 m, vitesse v1. Energie mécanique Em1 . Position 2, ballon remoné : vitesse nulle, altitude h = 1,0 m. Energie mécanique Em2 = Em1 -2,5. mg h +½mv12 -2,5 = mg h. ½mv12 =2,5 ; v1 = [2 x2,5 / 0,600]½ =2,9 m /s. 3. Entendre l’arbitre lors d’un match Le basket-ball est un sport dans lequel le public peut se manifester bruyamment à n’importe quel moment. Pour autant, l’arbitre, qui signale les fautes grâce à un sifflet, doit pouvoir être entendu par tous les joueurs. On admet que l’on peut distinguer un son très bref et aigu du bruit ambiant si son niveau sonore est supérieur d’au moins 3 dB à celui du bruit ambiant. Q16. On suppose que l’arbitre siffle au moment où est commise une faute. À cet instant, il est à une distance d1 = 20 m du joueur le plus éloigné sur le terrain et à une distance d2 = 1,0 m d’un joueur remplaçant assis sur un banc au bord du terrain. À l’aide d’un calcul, déterminer si le joueur remplaçant doit porter des protections auditives, sachant que le bruit ambiant est de l’ordre de 80 dB. Niveau sonore perçu par le joueur le plus éloigné : 80 +3 = 83 dB. Intensité sonore correspondante I1 = 10-12 x 108,3 =10-3,7 W m-2. Puissance sonore du sifflet : P = 4pd12 I1. I2 : intensité sonore pour le joueur remplaçant : I2 = P / (4pd22) = I1 (d1 / d2)2 =10-3,7 x(20 / 1)2 =0,08 W m-2. Niveau sonore L2 = 10 log (0,08 / 10-12)=109 dB, valeur supérieur au seuil de danger (90 dB). Le remplaçant doit porter des protections auditives.. ane.

menu