Exercice 1. 6 points.
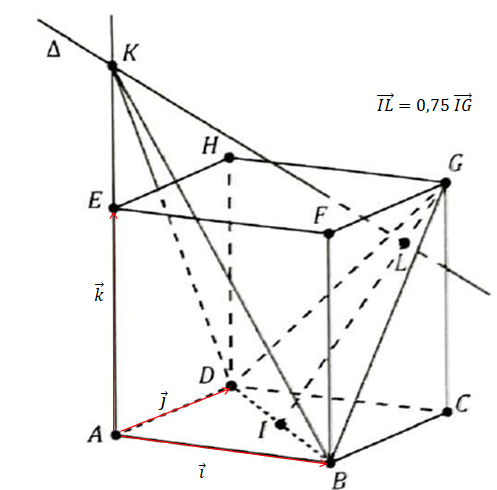
On considère le cube ABCDEFGH de côté 1. I est le milieu du segment BD.
 1. a
1. a Préciser les coordonnées des points D, B, I et G.
D(0 ; 1 ; 0) ; B (1 ; 0 ; 0) ; I(0,5 ; 0,5 ; 0) ; G ( 1 ; 1 ; 1).
1.b. Montrer que les coordonnées du point L sont ( 7 /8 ; 7 /8 ; 3 /4).
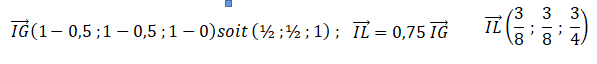
x
L-x
I = 3 /8 ;
xL=xI + 3 /8= 1/2 +3 /8 =7/8.
yL-yI = 3 /8 ; yL=yI + 3 /8= 1/2 +3 /8 =7/8.
zL-zI = 3 /4 ; zL=xzI + 3 /4= 0 +3 /4 =3/4.
2. Vérifier qu'une équation cartésienne du plan ( BDG) est x+y-z-1=0.
B appartient à ce plan : ax
B+by
B+c z
B+d = 0 ; a+d=0 ; d = -a.
D appartient à ce plan : axD+byD+c zD-a = 0 ; b-a=0 ; a = b.
G appartient à ce plan : axG+ayG+c zG-a = 0 ; a+c=0 ; c = -a.
ax+ay-az-a=0 soit x+y-z-1=0.
3. On considère la droite
D perpendiculaire au plan (BDG) passant par L.
a. Justifier qu’une représentation paramétrique de la droite
D est :
x =
7
/8
+ t
; y =
7/
8
+ t
; z =
3
/4
− t avec t réel.
Coordonnées d'un vecteur normal au plan (BDG) = coordonnées d'un vecteur directeur de la droite (
D) : (1 ; 1 ; -1)
Par suite x = t+x
L = t+7/8 ; y = t+y
L = t+7 /8 ; z = -t +z
L = -t +3/4 avec t réel.
b. Montrer que les droites
D et (AE) sont sécantes au point K de coordonnées (
0 ; 0 ;
13/
8
¶
.
Représentation paramétrique de la droite (AE) :
x =0 ; y =0 z =k+1 avec k réel.
Dans l'hypothèse où les droites
D et (AE) sont sécantes en K :
xK=7
/8
+ t
=0 ;t = -7 /8 ;
yK=7/
8
+ t =0 est vérifié.
zK=3/4-t=3/4+7/8=13/8. L'hypothèse est valide.
c. Que représente le point L pour le point K ? Justifier la réponse.
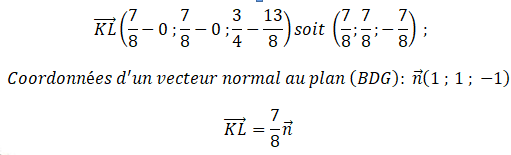
L est le projeté orthogonal du point K sur le plan ( BDG).
4. a. Calculer la distance KL.
KL
2 =(7/8)
2 +(7/8)
2 +(3/4-13/8)
2=
(7/8)2 +(7/8)2 +(-7/8)2 = 3x(7/8)2 ;
KL = 7 / 8 x3½.
b. On admet que le triangle DBG est équilatéral. Montrer que son aire est égale à 3
½ /2.
Base GBD ; hauteur relative à cette base GI ;
BD = 2
½ ; GI
2= 0,5
2 +0,5
2 +1
2 =1,5 ; GI = (3/2)
½.
Aire du triangle DBG : BD xGI / 2 = 2
½x
(3/2)½ / 2 =3
½ /2.
.
c. En déduire le volume du tétraèdre KDBG.
Aire du triangle DBG x KL / 3 =3½ /2 x7 / (8 x3 )x3½=7 / 16.
.
5. On désigne par a un réel appartenant à l’intervalle ]0 ; +∞[ et on note K
a le point de
coordonnées (0 ; 0 ; a).
a. Exprimer le volume V
a de la pyramide ABCDK
a en fonction de a.
Aire de base = aire du carré ABCD = 1.
Hauteur :KA = a.
Volume = aire de base x hauteur / 3 = a /3.
b. On note
Da la droite de représentation paramétrique :
x = t
′
; y = t
′
; z = −t
′ + a
où t
′ est un réel.
On appelle I
a le point d’intersection de la droite
Da avec le plan (BDG).
Montrer que les coordonnées du point L
a sont (
a +1)/
3
;
(a +1)/
3
;
(2a −1)/
3.
L
a appartient à la fois au plan (BDG) et à la droite
Da.
xIa+yIa-zIa-1=0.;
t'+t'+t'-a-1=0 ; 3t'-a=1 ; t' =(1+a)/3.
xIa=.(1+a) / 3 ; yIa=.(1+a) / 3 ; zIa= -(1+a) / 3 +a=(2a −1)/
3.
c. Déterminer, s’il existe, un réel strictement positif a tel que le tétraèdre GDBK
a
et la pyramide ABCDKa sont de même volume.
Volume Va de la pyramide ABCDKa = a /3.
Volume V du tétraèdre GDBKa :
Aire du triangle DBG x KaLa / 3 =3½ /2 xKaLa / 3= 3½ x KaLa / 6.
KaLa2 =(a+1)2/9 +(a+1)2/9 +(-a-1)2/ 9=(a+1)2 / 3 ; KaLa =(a+1) / 3½.
V=(a+1) / 6.
Egalité des volumes :
(a+1) / 6 = a /3 ; (a+1) / 2 = a ; a =1.
Il existe un réel positif tel le tétraèdre GDBKa
et la pyramide ABCDKa sont de même volume.
Exercice 2. 5 points.
Partie A.
Un artisan crée des bonbons au chocolat dont la forme rappelle le profil de la montage
locale représentée. La base d’un tel bonbon est modélisée par la surface grisée,
définie ci-dessous dans un repère orthonormé d’unité 2 cm.

Cette surface est délimitée par l’axe des abscisses et la représentation graphique notée C
f de la fonction f définie sur [−1 ; 1] par :f (x) = (1−x
2)e
x .
L’objectif de cette partie est de calculer le volume de chocolat nécessaire à la fabrication d’un bonbon au chocolat.
1. a. Justifier que pour tout x appartenant à l’intervalle [−1 ; 1] on a f (x)
>0.
Le terme en exponentielle est strictement positif.
(1-x
2) est positi ou nul.
(1−x2)ex > 0.
b. Montrer à l’aide d’une intégration par parties :
On pose u = 1-x2 ; v' = ex ; u' = -2x ; v = ex.
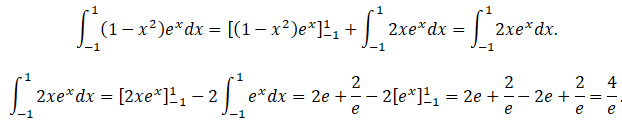
2. Le volume V de chocolat, en cm3, nécessaire à la fabrication d’un bonbon est donné par :
V = 3×S
où S est l’aire, en cm2, de la surface colorée.
En déduire que ce volume V , arrondi à 0,1 cm3 près, est égal à 4,4 cm3.
V = 3 x4 /e ~4,4 cm3.
Partie B.
On s’intéresse maintenant au bénéfice réalisé par l’artisan sur la
vente de ces bonbons au chocolat en fonction du volume hebdomadaire des
ventes.
Ce bénéfice peut être modélisé par la fonction B définie sur l’intervalle [0,01 ; +∞[ par :
B(q)= 8q2[2−3 ln(q)]−3.
Le bénéfice est exprimé en dizaines d’euros et la quantité q en centaines de bonbons.
On admet que la fonction B est dérivable sur [0,01 ; +∞[. On note B′ sa fonction dérivée.
1. a. Déterminerla limite de B(q) en plus l'infini.
ln(q) tend vers + oo ; -ln(q) tend vers -oo ; 2-3 ln(q) tend vers -oo.
q2 tend vers +oo ; par produit des limites B(q) tend vers - oo.
b. Montrer que, pour tout q >0,01, B′(q)= 8q(1−6 ln(q)).
On pose u = 8q2 et v = 2-3 ln(q).
u' = 16q ; v' = -3 /q.
u'v+v'u = 16q(2-3ln(q)) -24q =8q-48 q ln(q)=8q(1-6 ln(q)).
c. Étudier le signe de B′(q), et en déduire le sens de variation de B sur [0,01 ; +∞[.
Dresser le tableau de variation complet de la fonction B.
8 q >0 ; B'(q) a le signe de 1-6 ln(q).
Si q = exp(1/6), B'=0.
Si q < exp(1/6), B' > 0 et B(q) est strictement croissante.
Si q > exp(1/6), B' < 0 et B(q) est strictement décroissante.
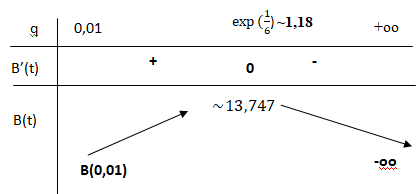
d. Quel est le bénéfice maximal, à l’euro près, que peut espérer l’artisan ?
8 x(exp(1/6))2 [2-3 ln(exp(1/6)]-3 ~11,16 x1,5-3~13,747 dizaines d'euros.
2. a. Montrer que l’équation B(q) = 10 admet une unique solution ß sur l’intervalle [1,2 ; +∞[.
Donner une valeur approchée de ß à 10−3 près.
La fonction B est continue car dérivable et strictement décroissante sur l(intervalle [1,18 ; +oo[.
De plus B(1,18) ~13,7 et B(Q) tend vers -oo si q tend vers plus l'infini.
D'après le théotème de la bijection, l'équation B(q) = 10 admet une unique solution sur l’intervalle [1,2 ; +∞[.
La calculatrice donne ß ~1,558.
b. On admet que l’équation B(q)= 10 admet une unique solution a sur [0,01 ; 1,2[.
On donne a ≈ 0,757.
En déduire le nombre minimal et le nombre maximal de bonbons au
chocolat à vendre pour réaliser un bénéfice supérieur à 100 euros.
Le nombre de bonbons est compris entre 76 et 155.