Observation
d'un avion en vol,
bac Métropole 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Le trafic aérien est source de
fascination pour beaucoup de gens. Notre observation se limite souvent
à la traînée
de l’avion dans le ciel ou, plus récemment, à un suivi en direct
(trajectoire, vitesse, altitude) grâce à des applications en ligne.
L’objectif de cet exercice est d’étudier l’observation, avec une
lunette astronomique afocale commerciale, de certains
détails de la structure d’un avion de type A312 en vol, puis de
déterminer la vitesse de cet avion en phase
d’atterrissage grâce à un enregistrement du son émis par le moteur.
Données :
Les valeurs du grossissement G de la lunette astronomique utilisée
sont comprises entre 16 et 48 ;
un observateur peut distinguer deux points différents A et B d’un
objet si l’angle sous lequel ces deux points sont vus depuis le
point d’observation (voir figure ci-dessous)est supérieur ou égal à
3,0×10–4 rad ;
quelques données concernant un avion A312 :
- longueur de l’avion : L = 44,5 m ;
- altitude de vol de croisière de l’avion : h = 10,4 km ;
- vitesse de vol de croisière de l’avion : v = 863 km·h–1 ;
- hublot de l’avion A312 : largeur 23 cm ; hauteur 33 cm.
1. Observation d’un avion A312 avec une lunette astronomique.
Q1. Donner la définition d’une lunette afocale.
L'image d'un objet situé à l'infini se trouve aussi à l'infini. Le
faisceau incident est parallèle ; le faisceau qui émerge est aussi
parallèle.
Q2. Sur le schéma placer le foyer objet F2 puis le foyer image F '2 de l’oculaire de la lunette astronomique.
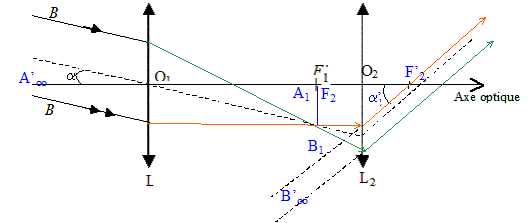
L’avion vole à la verticale de l’observateur et se trouve donc à la distance h de celui-ci.
Sur le schéma les extrémités avant et arrière de l’avion observé sont
respectivement modélisées par les points A∞ et B∞, situés à une très grande distance de l’observateur.
Q3. Construire, sur
le schéma, la marche des deux rayons lumineux issus de B∞ qui émergent
de la lunette, en faisant apparaître l’image intermédiaire A1B1.
L’angle a désigne l’angle sous lequel l’avion est observé à l’oeil nu. L’angle sous lequel l’avion est observé au travers
de l’oculaire de la lunette astronomique est nommé a'.
Q4. Vérifier à l’aide d’un calcul que l’on peut distinguer, à l’oeil nu, l’avant de l’avion de sa queue.
a =L / h = 44,5 / (10,4 103) =4,3 10-3 rad > 3,0×10–4 rad ; on peut distinguer l'avant de l'avion de sa queue.
Q5. Rappeler l’expression du grossissement G d’une lunette astronomique.
G = a ' / a.
Q6. Déterminer si on peut distinguer l’un de l’autre les deux bords verticaux d’un hublot de l’avion, à l’aide de la
lunette astronomique étudiée.
a = 0,23 / (10,4 103) =2,2 10-5 rad.
a' est compris entre 2,2 10-5 x16 =3,5 10-4 rad et 2,2 10-5 x48 =1,1 10-3 rad.
3,0×10–4
rad appartient à cet intervalle : à l'aide de la lunette, certaines
valeurs du grossissement permettent de distinguer les deux bords du
hublot.
|
...
|
....
|
2. Détermination de la vitesse d’un avion A312 en phase d’atterrissage
Au voisinage de l’aéroport, un observateur enregistre le son du moteur
de l’avion passant au-dessus de lui lors de sa phase d’atterrissage.
L’observateur est supposé fixe lors de l’enregistrement du son.
L’analyse du signal sonore enregistré permet de déterminer les fréquences des signaux reçus par l’observateur.
Lorsque l’avion s’avance en direction de l’observateur la fréquence mesurée est fA = 2,2 kHz, et lorsqu’il s’éloigne la fréquence est fE = 1,5 kHz.
Q7. Donner le nom du phénomène mis en jeu dans cette expérience.
Effet Doppler.
On note f0 la fréquence du signal émis par la source
immobile, c la vitesse du son dans l’air dans les conditions de
l’expérience et v la vitesse de l’avion par rapport au sol. On donne c
= 345 m·s–1.
Q8. Parmi les propositions A, B, C et D suivantes, choisir et recopier
sur la copie la proposition correcte. Expliquer pourquoi les autres
propositions sont à écarter.
A est fausse.
fA = c / (c-v) ; fE = c / (v+c).
Une fréquence s'exprime en hertz ; c / (c±v) rapport de deux vitesses, est sans dimension.
B est vraie.
fA = f0 c/(c-v) ; fE = f0 c /(c+v)
fA est bien supérieure à f0 et fE est inférieure à f0.
C est fausse.
fA = f0 c/(c+v) ; fE = f0 c /(c-v)
fA est inférieure à f0 et fE est supérieure à f0.
D est fausse.
fA = f0 c/(c-2v) ; fE = f0 c /(c+v).
Présence de 2 v ; c-2v doit être positif.
Q9. Déterminer la vitesse v de l’avion, exprimée en km·h–1, lors de cet atterrissage. Commenter.
fA = f0 c/(c-v) ; fE = f0 c /(c+v).
fA / fE =(c+v) / (c-v) ; 2,2 / 1,5 =1,467 =(345+v) /(345-v).
1,467(345-v) = 345 +v ;
506 -1,467 v = 345 +v ; 2,467 v = 131 ; v = 65,26 m /s = 65,26 x3,6 ~235 km /h.
|
ane.
|
|
|