Vol en mongolfière, thermique,  bac Métropole 09 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... 1. L’envol de la montgolfière Une montgolfière se compose de trois parties principales : une enveloppe dont le volume est considéré constant, un système de chauffage (brûleur avec réservoir de carburant) et une nacelle. Q1. Montrer que la valeur de la masse molaire Mair de l’air est voisine de 29×10–3 kg·mol–1. Diazote : M= 28 g/mol ; 80 % de l'air ; 0,80 x28 =22,4 g. Dioxygène : M = 32 g /mol ; 20 % de l'air ; 0,2 x32 =6,4 g Total : 22,4 +6,4 =28,8 g / mol. Q2. En exploitant l’équation d’état des gaz parfaits, exprimer littéralement la masse mint de l’air contenu à l’intérieur de l’enveloppe en fonction de la pression pint de l’air à l’intérieur, du volume V de l’enveloppe, de la masse molaire Mair de l’air, de la constante R des gaz parfaits et de la température Tint de l’air situé à l’intérieur de l’enveloppe. Pint V = n R Tint ; n = mint / Mair ; Pint V = mint / MairR Tint ; mint =Pint V Mair /(R Tint ). Q3. Exprimer le poids total du système {montgolfière + air intérieur}, noté Ptotal, en fonction des masses mens =500 kg et mint. Ptotal=( mens+mint) g. Q4. Calculer la valeur de la poussée d’Archimède F qui s’exerce sur le système {montgolfière + air intérieur}, au niveau du sol. Volume invariable de l'enveloppe V = 2,5 103 m3. Température de l'air au niveau du sol : 21°C. F = rair ext V g =1,2 x 2,5 103 x9,8 =2,9 104 N. Q5. Montrer que l’expression de la valeur de la température minimale Tmin de l’air à l’intérieur de l’enveloppe pour que la montgolfière puisse décoller est : Tmin = Pint V Mair /(R( F /g-mens)). Calculer la valeur de Tmin. La poussée doit être supérieure au poids. A la limite du décollage : Poussée F = poids du volume d'air contenu dans l'enveloppe = min g = Pint V Mair g /(R Tint ). P =F = ( mens+mint) g =(mens+Pint V Mair  /(R Tint )) g. F / g =mens+Pint V Mair  /(R Tint ). F / g -mens=Pint V Mair  /(R Tint ). R Tint =Pint V Mair  / (F / g -mens). Tmin = Pint V Mair /(R( F /g-mens)). Tmin =1,0 105 x2,5 103 x 29 10-3 / (8,31( 2,943 104 /9,81-500))=349 K ou 349-273=76°C. On admet que la pression pint de l’air à l’intérieur de l’enveloppe est égale à la pression atmosphérique patm = 1,0×105 Pa. Alors que la montgolfière est retenue au sol par des sangles, le pilote actionne les brûleurs afin que la température de l’air intérieur de l’enveloppe soit supérieure à la température Tmin. À la date t = 0, les sangles sont détachées et la montgolfière, initialement immobile, commence son ascension verticale. À cet instant, la valeur de la poussée d’Archimède exercée sur le système est égale à F = 2,9×104 N et la masse totale du système {montgolfière + air intérieur} est mtot = 2,8×103 kg. Dans une modélisation simplifiée, on ne tient compte que de la poussée d’Archimède et du poids pour étudier le mouvement du ballon. On suppose également que les valeurs de ces forces restent inchangées au cours du temps. Q6. Déterminer la valeur de l’accélération du système {montgolfière + air intérieur}. Calculer ensuite la valeur de sa vitesse au bout de 10 s puis au bout de 1 minute d’ascension. La mongolfière est soumise à son poids, vertical, vers le bas, et à la poussée d'Archimède verticale vers le haut. La seconde loi de Newton écrite sur un axe vertical orienté vers le haut conduit à : F-P = mtot a ; F-mtot g = mtot a. a = F /mtot -g=2,9 104 /(2,8 103) -9,81 = 0,547 ~0,55 m /s2. La vitesse est une primitive de l'accélération : v = at + cste. La vitesse initiale étant nulle : v = at = 0,547 t. Au bout de 10 s : v= 5,47 ~5,5 m /s ou 5,5 x3,6 ~20 km / h.. Au bout d'une minute : v = 0,547 x60 = 32,8 ~33 m /s ou 32,8 x3,6 ~120 km/h. Q7. Commenter les résultats obtenus à la question précédente et proposer une piste d’amélioration du modèle. Ces deux valeurs sont invraissemblables. Il faut pprendre en compte les frottements sur les couches d'air. 2. Une enveloppe de montgolfière plus performante. Des entreprises spécialisées dans la conception des montgolfières ont développé une nouvelle gamme d’enveloppes. Contrairement aux enveloppes traditionnelles, constituées d’une simple couche de nylon, les nouveaux modèles d’enveloppes sont constitués d’une double couche de nylon. Entre les deux épaisseurs de nylon, une couche d’air permet de limiter le transfert thermique vers l’extérieur de l’enveloppe. La consommation de carburant est ainsi réduite. Données :  résistance thermique d’une enveloppe simple couche : Rth,1 = 3,0×10–4 K·W–1 ;  on rappelle que le flux thermique F1 à travers l’enveloppe simple couche du ballon, de l’intérieur vers l’extérieur, est donné par la relation : F1=(qint-qext) / Rth,1. où qext = 21 °C est la température de l’air extérieur et où qint = 106 °C est la température de l’air intérieur. Q8. Préciser, en justifiant, le sens du flux thermique à travers l’enveloppe simple couche du ballon. Le flux thermique est dirigé de l'intérieur ( air chaud) vers l'extérieur ( air froid). Q9. Calculer la valeur du flux thermique F1 à travers une enveloppe simple couche. F1=(106-21)/(3,0×10–4)=2,8 105 W = 2,8 102 kW. Q10. Le flux thermique  F2 à travers l’enveloppe à double paroi est  165 kW. Commenter. 280-165=115 kW soit 115 / 280 * 100 =41 %. Le flux thermique est réduit et on économise le carburant. ... .... 3. Une gourde en aluminium à bord de la montgolfière.  Le pilote de la montgolfière emporte avec lui une gourde en aluminium contenant une boisson chaude. On étudie en laboratoire l’évolution temporelle de la température du système {gourde + boisson} et on modélise le transfert thermique entre ce système et l’extérieur par la loi de Newton, rappelée dans les données cidessous. 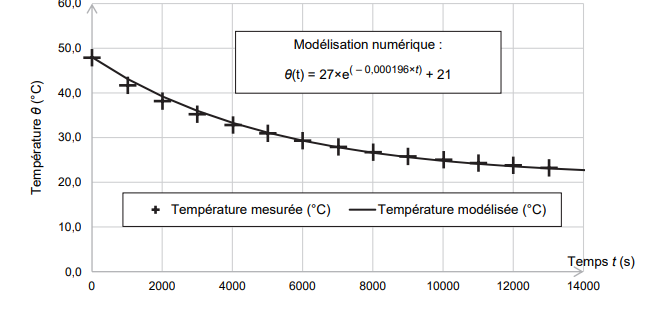La température du système à la date t est notée q(t). À la date t = 0 correspondant au début de l’expérience, la température du système est q0 = 48 °C. Données :  capacité thermique du système étudié : C = 2,1×103 J·K–1 ;  surface totale de la gourde exposée à l’air : S = 0,042 m2 ;  la température de l’air extérieur est supposée constante pendant toute la durée de l’expérience et égale à qext = 21 °C ;   la loi de Newton donne l’expression du flux thermique F (en W) reçu par le système {gourde + boisson}, à la température q(t), de la part de l’air extérieur, à la température qext : F = h·S·(qext – q(t)) où h est le coefficient d’échange thermique surfacique. Lors de l’expérience réalisée en laboratoire, l’utilisation d’un système d’acquisition informatisé permet d’obtenir l’évolution de la température du système au cours du temps. On considère deux instants voisins t et t + Dt, la durée Dt est supposée faible devant une durée caractéristique d’évolution de la température du système. Q11. Montrer que la température du système vérifie la relation : q(t+Dt ) – q(t) = h · S · (qext – q (t))·Dt  / C . Energie échangée  entre la gourde et l'air extérieur pendant la durée Dt : C(q(t+Dt ) – q(t) )=F Dt= h·S·(qext – q(t)) Dt. q(t+Dt ) – q(t)=h · S · (qext – q (t))·Dt  / C . F = h·S·(qext – q(t)) Dt =C À partir du résultat précédent, on montre que la température q(t) du système lors de son refroidissement vérifie l’équation différentielle suivante : dq(t) dt + q(t) / t = qext/ t avec t = C h·S le temps caractéristique du système. L’équation différentielle précédente admet des solutions générales de la forme q(t) = A·exp(-t /t) + B. Q12. Déterminer les expressions littérales des constantes A et B en fonction de q0 et qext puis calculer leurs valeurs. Commenter. A t=0 :  q0=A+B. Au bout d'un temps suffisamment grand : qext =B. Par suite A =q0-qext .  Q13. Déterminer la valeur du temps caractéristique à partir de la modélisation numérique de la figure. t=1/0,000196~5,1 103 s.  Q14. En déduire la valeur du coefficient h d’échange thermique surfacique, puis commenter le résultat obtenu  C /(h·S) =5100 ; h =2,1 103 /(5,1 103 x0,042)~ 9,8 W K-1 m-2. Valeur comprise entre 5 et 10 : en accord avec une gourde placée hors des courants d'air. ane.

menu