Mathématiques, bac centres étrangers 2024 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1. 4 points. Affirmation 1 : Soit (E) l’équation différentielle : y’ – 2y = −6x + 1 La fonction f définie sur R par f(x))= e2x−6x+1 est une solution de l’équation différentielle (E). Faux. f '(x) =2e2x-6. Repport dans (E) : 2e2x-6-2e2x+12x-2= 12x-8 diffère de -6x+1. Affirmation 2 : On considère la suite (un) définie sur N par un=1+3/4+(3/4)2+⋯+(3/4)n. La suite (un) a pour limite +∞. Faux. Somme des termes d'une suite géométrique de raison 3/4 et de premier terme 1. un = (1-(3/4)n+1) / (1-3/4). -1 < 3/4 <1; donc (3/4)n tend vers zéro si n tend vers plus l'infini. un tend vers 4. Affirmation 3 : On considère la suite (un) définie dans l’affirmation 2. L’instruction suite(50) ci-dessous, écrite en langage Python, renvoie u50. Faux. def suite(k) S=0 for i in range k : S = S+(3/4)**k return S suite(50) renvoie u49 ; i varie de 0 à k-1. Affirmation 4 : Soit a un réel et f la fonction définie sur ]0;+∞[ par f(x)=a ln(x)-2x. Soit C la courbe représentative de la fonction f dans un repère orthonormé. Il existe une valeur de a pour laquelle la tangente à C au point d’abscisse 1 est parallèle à l’axe des abscisses. Vrai. Coefficient directeur de la tangente : f '(x) = a / x-2. f '(1) =a-2 ; f(1) = 0 si a = 2. Si a = 2, la tangente à la courbe C au point d'abscisse 1 est parallèle à l'axe des abscisses. Exercice 2 ( 5 points). Au cours d’une séance, un joueur de volley-ball s’entraîne à faire des services. La probabilité qu’il réussisse le premier service est égale à 0,85. On suppose de plus que les deux conditions suivantes sont réalisées : • si le joueur réussit un service, alors la probabilité qu’il réussisse le suivant est égale à 0,6 ; • si le joueur ne réussit pas un service, alors la probabilité qu’il ne réussisse pas le suivant est égale à 0,6. Pour tout entier naturel n non nul, on note Rn l’évènement « le joueur réussit le n-ième service ». Partie A : On s’intéresse aux deux premiers services de l’entraînement. 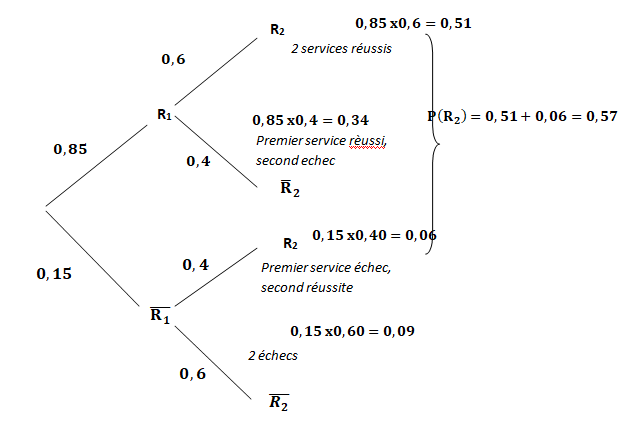1. Représenter la situation par un arbre pondéré. 2. Démontrer que la probabilité de l’événement R2 est égale à 0,57. 3. Sachant que le joueur a réussi le deuxième service, calculer la probabilité qu’il ait raté le premier. PR2(non R1) =P(non R1 n R2) / P(R2)= 0,15 x0,4 / 0,57 =6 / 57 = 2 / 19. 4. Soit Z la variable aléatoire égale au nombre de services réussis au cours des deux premiers services. a. Déterminer la loi de probabilité de Z (on pourra utiliser l’arbre pondéré de la question 1). P(Z=0 ) = 0,09. P(Z=1) =0,34 +0,06=0,4. P(Z=2 ) =0,51. b. Calculer l’espérance mathématique E(Z) de la variable aléatoire Z. Interpréter ce résultat dans le contexte de l’exercice. E(Z) = 0 xP(Z =0) +1 xP(Z=1)  +2 x P(Z=2) = 0,4 +2 x0,51=1,42. Partie B : On s’intéresse maintenant au cas général. Pour tout entier naturel n non nul, on note xn la probabilité de l’évènement Rn. 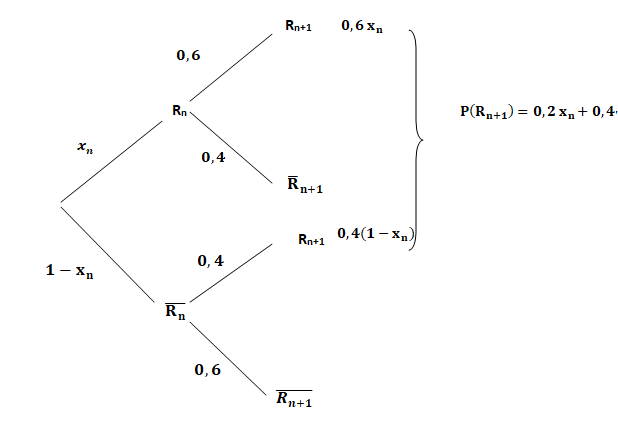1.a. Donner les probabilités conditionnelles Pnon Rn(non Rn+1) et PRn(Rn+1) . PRn(Rn+1)  = 0,6 ; Pnon Rn(non Rn+1) = 0,6 d'après l'énoncé. b. Montrer que, pour tout entier naturel non nul n, on a : x𝑛+1=0,2xn+0,4. x𝑛+1=P(Rn+1). D'après la formule des probabilités totales : P(Rn+1) =P(Rn n Rn+1)+ Pnon Rn n Rn+1). P(Rn+1) =0,6 xn+0,4(1-xn)=0,2 xn+0,4. 2. Soit la suite (un) définie pour tout entier naturel n non nul par un=xn−0,5 a. Montrer que la suite (un) est une suite géométrique. un+1=xn+1−0,5=0,2 xn +0,4-0,5 =0,2 xn -0,1=0,2(xn-0,5)= 0,2 un. La suite est géométrique de raison 0,2 et de premier terme u0 = 0,85 -0,5 = 0,35. b. Déterminer l’expression de xn en fonction de n. En déduire la limite de la suite (xn). un = 0,35 x0,2n ; xn= 0,35 x0,2n +0,5. -1 < 0,2 < 1 donc 0,2n tend vers zéro si n tend vers +oo. xn tend vers 0,5. c. Interpréter cette limite dans le contexte de l’exercice. Le joueur finira par réussir un service sur deux ... .... Exercice 3. 7 points. Un organisme certificateur est missionné pour évaluer deux appareils de chauffage, l’un d’une marque A et l’autre d’une marque B. Les parties 1 et 2 sont indépendantes. Partie 1 : appareil de la marque A. À l’aide d’une sonde, on a mesuré la température à l’intérieur du foyer d’un appareil de la marque A. On a représenté, ci-dessous, la courbe de la température en degrés Celsius à l’intérieur du foyer en fonction du temps écoulé, exprimé en minutes, depuis l’allumage du foyer. 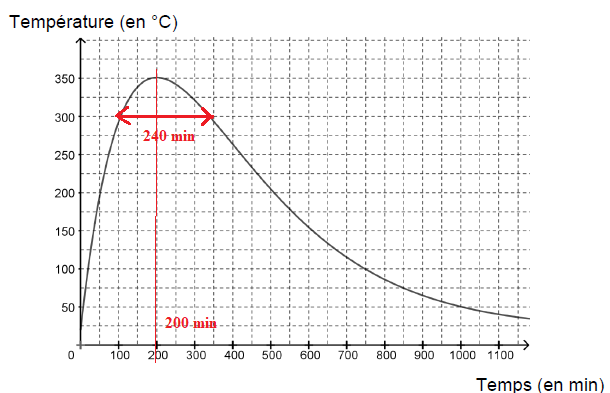Par lecture graphique : 1. Donner le temps au bout duquel la température maximale est atteinte à l’intérieur du foyer. 200 min. 2. Donner une valeur approchée, en minutes, de la durée pendant laquelle la température à l’intérieur du foyer dépasse 300°C. 240 min. 3. On note f la fonction représentée sur le graphique. Estimer la valeur de l'intégrale suivante. Interpréter le résultat. 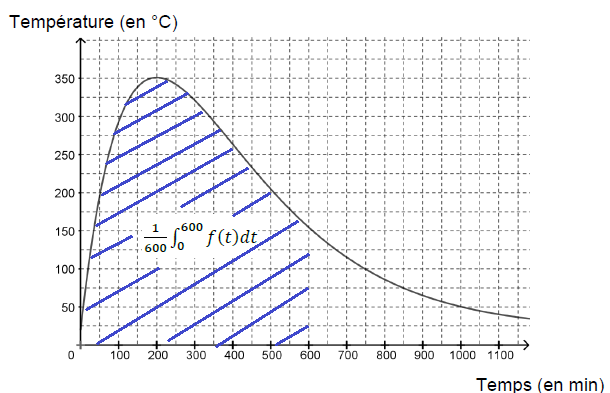Aire d'un petit carré : 50 x25 =1250 ; aire hachurée : 120 x1250 =150 000. 150 000 / 600 =250 °C. Au cours des 600 premières minutes, la température moyenne du foyer est de 250°C. Partie 2 : étude d’une fonction. Soit la fonction g définie sur l’intervalle [0 ;+∞[ par g(t)=10t e-0,01t+20 1. Déterminer la limite de g en +∞. En plus l'infini, le terme en exponentielle tend vers zéro ; g(t) tend vers 20. 2. a. Montrer que pour tout t appartenant à  [ 0 ; +∞ [ , g'(t) = (-0,1t +10) e-0,01t. On pose u =10 t et v = e-0,01t. u' = 10 ; v' = -0,01 e-0,01t. u'v+v'u = 10 e-0,01t-0,1t e-0,01t. b. Étudier les variations de la fonction g sur [ 0 ; +∞ [ et construire son tableau de variations. e-0,01t étant positif, le signe de g'(t) est celui de 10-0,1t. 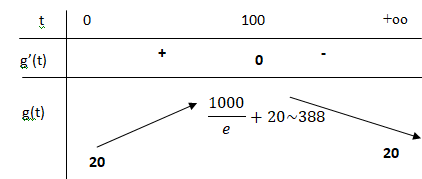3. Démontrer que l’équation g(t)=300 admet exactement deux solutions distinctes sur [ 0 ; +∞ [. En donner des valeurs approchées à l’unité. La fonction g(t) est continue car dérivable et strictement croissante sur [0 ; 100]. g(0 ) = 20 ; g(100) ~388. D'après le théorème de la bijection, g(x) = 300 admet une solution unique sur [0 ; 100]. g(100 ) ~388 ; g tend vers 20 si t tend vers +oo. D'après le théorème de la bijection, g(x) = 300 admet une solution unique sur [100 ; +oo[. g(t) = 300 admet deux solutions sur [0 ; +oo[. La calculatrice donne ; 43 et 193. 4. À l’aide d’une intégration par parties, calculer l'intégrale suivante. On pose u= 10t ; u' = 10 ; v'=e-0,01t ; v = -100e-0,01t . 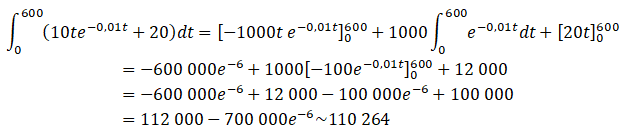Partie 3 : évaluation Pour un appareil de la marque B, la température en degrés Celsius à l’intérieur du foyer t minutes après l’allumage est modélisée sur [0;600] par la fonction g. L’organisme certificateur attribue une étoile par critère validé parmi les quatre suivants : - Critère 1 : la température maximale est supérieure à 320°C. - Critère 2 : la température maximale est atteinte en moins de 2 heures. - Critère 3 : la température moyenne durant les 10 premières heures après l’allumage dépasse 250 °C. - Critère 4 : la température à l’intérieur du foyer ne doit pas dépasser 300°C pendant plus de 5 heures. Chaque appareil obtient-il exactement trois étoiles ? Justifier votre réponse.  Appareil A : tmaxi =350°C. la température maximale est atteinte au bout de 200 min( plus de  2 heures).. Au cours des 600 premières minutes, la température moyenne du foyer est de 250°C. La température à l’intérieur du foyer dépasse 300°C pendant 240 minutes. Donc 3 étoiles validées.  Appareil B : tmaxi =388°C. la température maximale est atteinte au bout de 100 min( moins de  2 heures).. Au cours des 600 premières minutes, la température moyenne du foyer est de  : 110 264 / 600 ~184 °C. La température à l’intérieur du foyer dépasse 300°C pendant 193-43=150 minutes. Donc 3 étoiles validées. Exercice 4. 4 points. On modélise un passage de spectacle de voltige aérienne en duo de la manière suivante : • on se place dans un repère orthonormé, une unité représentant un mètre ; • l’avion n°1 doit relier le point O au point A(0 ; 200 ; 0) selon une trajectoire rectiligne, à la vitesse constante de 200 m/s ; • l’avion n°2 doit, quant à lui, relier le point B(−33 ;75 ; 44) au point C(87 ; 75 ; −116) également selon une trajectoire rectiligne, et à la vitesse constante de 200 m/s. • au même instant, l’avion n°1 est au point O et l’avion n°2 est au point B. 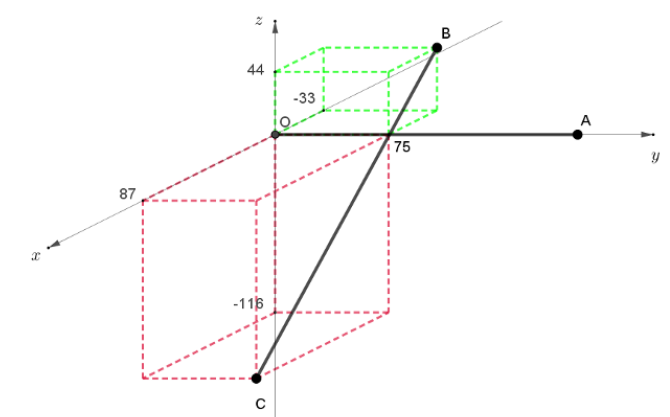1. Justifier que l’avion n°2 mettra autant de temps à parcourir le segment [BC] que l’avion n°1 à parcourir le segment [OA]. BC2 =(87-(-33))2 + (75-75)2 +(-116-44)2 =14 400+25 600=40 000 ; BC =200. Durée du parcours BC :200 /200 = 1 s. OA = 200 m ; durée du parcours OA : 200 / 200 = 1 s. 2. Montrer que les trajectoires des deux avions se coupent. Coordonnées du vecteur OA : 0 ; 200  ; 0. Représentation paramétrique de la droite (OA) : x = 0 ; y = 200 t ; z = 0 avec t réel. Coordonnées du vecteur BC : (120 ; 0 ; -160). Représentation paramétrique de la droite (BC) : x = 120 k +xB=120 k -33   y = yB =75  ; z = -160k +zB =-160 k+44 avec k réel. Dans l'hypothèse où les droites se coupent : 120k-33 = 0 soit k = 33 / 120 = 11 / 40. 20 t = 75 ; t = 75 /20 =15 /4. 0 =-160k+44 ; 0 =-160 x11 / 40 +44 =0 est bien vérifié. Les droites sont sécantes au point de coordonnées G (0 ; 75 ; 0). 3. Les deux avions risquent-ils de se percuter lors de ce passage ? AG = 200-75=125. L'avion 1 atteint le point G au bout de 125 / 200 =0,625 s. CG2 =872+02+1162=21 025 ; CG =145 m. L'avion 2 atteint le point G au bout de 145 / 200 =0,725 s. Les deux avions ne risquent pas de se percuter. ane.

menu