Mathématiques,
bac étrangers 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. 5 points.
Un sac opaque contient huit jetons numérotés de 1 à 8, indiscernables
au toucher.
À trois reprises, un joueur pioche un jeton dans ce sac, note son
numéro, puis le remet dans le sac.
Dans ce contexte, on appelle « tirage » la liste ordonnée des trois
numéros obtenus.
Par exemple, si le joueur pioche le jeton numéro 4, puis le jeton
numéro 5, puis le jeton numéro 1, alors le tirage correspondant est (4; 5; 1).
1. Déterminer le nombre de tirages possibles.
83 = 512.
2. a. Déterminer le nombre de tirages sans répétition de numéro.
Cela revient à fzire un tirage sans remise. Il y a donc : 8! /(8-3)! =8 x7 x6 = 336 tirages.
b. En déduire le nombre de tirages contenant au moins une répétition de
numéro.
C'est la différence des deux résultats précédents.
512-336 = 176.
On note X1 la variable aléatoire égale au numéro du premier jeton
pioché, X2 celle égale au numéro du deuxième jeton pioché et X3 celle égale au numéro du
troisième jeton pioché.
Puisqu’il s’agit d’un tirage avec remise, les variables aléatoires
X1,X2, et X3 sont indépendantes et suivent lamême loi de probabilité.
3. Établir la loi de probabilité de la variable aléatoire X1.
Situation d'équiprobabilité. La loi de probabilité de X1 est donnée par le tableau suivant :
xi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
P(X1 = xi)
|
1 /8
|
1 /8
|
1 /8
|
1 /8
|
1 /8
|
1 /8
|
1 /8
|
1 /8
|
4. Déterminer l’espérance de la variable aléatoire X1.
E(X1) =(1 +2 +3 +4 +5 +6 +7 +8) / 8 =4,5.
On note S = X1 + X2 + X3 la variable aléatoire égale à la somme des
numéros des trois jetons piochés.
5. Déterminer l’espérance de la variable aléatoire S.
E(S) = E(X1) + E(X2) + E(X3 ) = 3 E(X1) = 13,5.
6. Déterminer P(S = 24).
Cet événement n'est réalisé que par le tirage (8 ; 8 ; 8) soit une seule issue possible parmi 512 possibilités.
P(S=24) = 1 / 512.
7. Si un joueur obtient une somme supérieure ou égale à 22, alors il
gagne un lot.
a. Justifier qu’il existe exactement 10 tirages permettant de gagner un
lot.
Le nombre 24 est obtenu par la somme 8 +8 +8.
Le nombre 23 est obtenu par la somme 7 +8 +8. Il yr a trois tirages différents ( 7 ; 8 ; 8) ; (8 ; 7 ; 8) et (8 ; 8 ; 7).
Le nombre 22 est obtenu par la somme 7 +7 +8 ou bien 6 +8 +8 ; il a six tirages différents :
(6 ; 8 ; 8) ; (8 ; 6 ; 8) ; (8 ; 8 ; 6) ; (8 ; 7 ; 7) ; (7 ; 8 ; 7) et (7 ; 7 ; 8).
b. En déduire la probabilité de gagner un lot.
10 tirages favorables sur 512 possibles : 10 / 512 = 5 / 256.
EXERCICE 2 6 points
On considère la fonction f définie sur l’intervalle ]−∞; 1[ par f (x) =ex/(x-1).
On admet que la fonction f est dérivable sur l’intervalle ]−∞; 1[ .
On appelle C sa courbe représentative dans un repère.
1. a. Déterminer la limite de la fonction f en 1.
ex tend vers e et le dénominateur tend vers 0-. f(x) tend vers -oo.
b. En déduire une interprétation graphique.
La droite d'équation x = 1 est asymptote verticale à la courbe.
2. Déterminer la limite de la fonction f en -oo.
ex tend vers zéro et le dénominateur tend vers -oo. f(x) tend vers zéro.
3. a. Montrer que pour tout réel x de l’intervalle ]−∞; 1[ , on a :
f ′(x) =(x −2)ex /(x −1)2 .
On pose u = ex et v = x-1 ; u' = ex ; v' = 1 ; (u'v-v'u) / v2 =[(x-1)ex-ex)] /(x-1)2 =(x −2)ex /(x −1)2 .
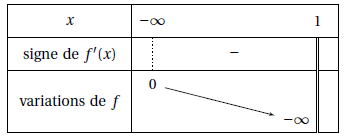
b. Dresser, en justifiant, le tableau de variations de la fonction f sur l’intervalle ]−∞; 1[.
La dérivée possède le signe de x-2. Sur ]−∞; 1[ , la dérivée est strictement négative et f(x) est strictement décroissante.
4. On admet que pour tout réel x de l’intervalle ]−∞; 1[, on a
f ′′(x) =(x2-4x+5)ex / (x-1)3.
a. Étudier la convexité de la fonction f sur l’intervalle ]−∞; 1[.
On étudie le signe de f "(x) :
(x-1)3 < 0 ; ex >0 ; le signe de f "(x) est celui de x2-4x+5.
Discriminant D = 42 -4x5 = -4. pas de racines réelles.
Le coefficient de x2 étant positif, x2-4x+5 > 0.
f (x) est strictement négative sur ]-oo ; 1[. La fonction f est concave sur cet intervalle.
b. Déterminer l’équation réduite de la tangente T à la courbe C au point d’abscisse 0.
Coefficient directeur de cette tangente : f '(0) =-2.
y = -2x+b ; le point de coordonnées (0 ; f(0) = -1) appartient à la tangente :
-1 = b ; y = -2x-1.
c. En déduire que, pour tout réel x de l’intervalle ]−∞; 1[, on a : ex >(−2x −1)(x −1).
f est concave, la courbe C est située sous ses tangentes.
f(x) < -2x-1.
ex / (x-1) < -2x-1
x-1 étant négatif : ex > (x-1)(-2x-1)
5. a. Justifier que l’équation f (x) =−2 admet une unique solution a sur l’intervalle ]−∞; 1[.
La fonction est continue car dérivable sur cet intervalle.
f(x) est strictement décroissante de 0 à -oo.
-2 appartient à ]0 ; -oo[.
D'après le corrolaire du théorème des valeurs intermédiaires, l'équation f(x) = -2 admet une unique solution sur ]-oo ; 1[.
b. À l’aide de la calculatrice, déterminer un encadrement de a d’amplitude 10−2 .
f(0,31) = -1,98 ; f(0,32) = -2,03.
0,31 < a < 0,32.
|
...
|
....
|
EXERCICE 3 5 points
Le cube ABCDEFGH a pour arête 1 cm.
Le point I est lemilieu du segment [AB] et le point J est le milieu du segment [CG].
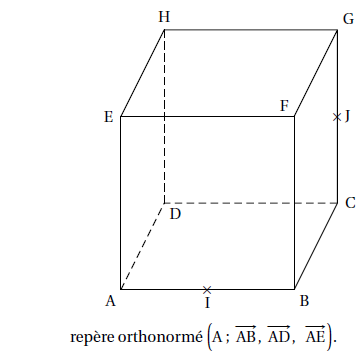
1. Donner les coordonnées des points I et J.
I( 0,5 ; 0 ; 0) ; J(1 ; 1 ; 0,5).
2. Montrer que le vecteur EJ est normal au plan (FHI).
On montre que ce vecteur est othogonal à deux vecteurs non colinéaires de ce plan.
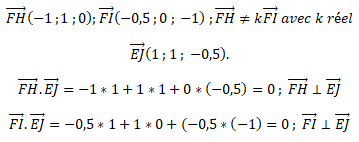
3. Montrer qu’une équation cartésienne du plan (FHI) est −2x −2y +z +1 = 0.
x+y-0,5z+d =0.
I appartient au plan (FHI) : 0,5 +0+0+d=0 ; d = -0,5.
x+y-0,5 z -0,5 = 0 ou -2x-2y+z+1=0.
4. Déterminer une représentation paramétrique de la droite (EJ).
Le vecteur Ej(1 ; 1 ; -0,5) est un vecteur directeur de cette droite : x = t+xE = t ; y = t+yE = t ; z = -0,5t +zE = -0,5t+1.
5. a. On note K le projeté orthogonal du point E sur le plan (FHI). Calculer ses coordonnées.
K est l'intersection du plan (FHI) et de la droite(EJ) orthogonale au plan et passant par E.
K(x ; y ; z) appartient à la droite (EJ) et au plan(FHI) :
-2t -2t+1-0,5t+1 = 0 ; -4,5t +2 =0 ; t = 4 / 9.
K(4 / 9 ; 4 / 9 ; 7 / 9).
b. Montrer que le volume de la pyramide EFHI est 1 /6 cm3.
On pourra utiliser le point L, milieu du segment [EF]. On admet que ce
point est le projeté orthogonal du point I sur le plan (EFH).
V = Base x hauteur / 3.
On prend le triangle EFH comme base ; La hauteur issue de I est
la droite (IL) ; la distance de I au plan(EFH) est la longueur IL.
Le triangle EFH est rectangle en E et son aire vaut : 1 x1 / 2 = 0,5.
Coordonnées de L ( 0,5 ; 0 ; 1) ; LI2 = (0,5-0,5)2 +(0-0)2+(1-0)2=1 ; IL = 1.
V =0,5 * 1 / 3 = 1 / 6 cm3.
c. Déduire des deux questions précédentes l’aire du triangle FHI.
On calcule le volume de cette pyramide à partir du triangle FHI comme base. EK sera la hauteur.
EK2 =(4 /9-0)2 +(4/9-0)2 +(7/9-1)2 =16 / 81 +16 / 81 +4 /81 =36 / 81 ; EK =6 /9 =2 /3.
Par suite 1 /6 = aire triangle FHI / 3 x2 /3 ; aire de ce triangle =1 /6 x3 x3 /2 = 9 /12 =3 /4 cm2.
EXERCICE 4 4 points
Partie A
On considère la fonction f définie sur l’intervalle [0 ; +∞[ par
f (x) =(x+1)½.
On admet que cette fonction est dérivable sur ce même intervalle.
1. Démontrer que la fonction f est croissante sur l’intervalle [0 ; +∞[.
f '(x) =½(x+1)-0,5 > 0 ; f est croissante sur cet intervalle.
2. Démontrer que pour tout nombre réel x appartenant à l’intervalle [0 ; +∞[ :
f (x)−x = (-x2+x+1) /((x+1)½+x).
3. En déduire que sur l’intervalle [0 ; +∞[ l’équation f (x) = x admet pour unique solution : l=(1+5½) / 2.
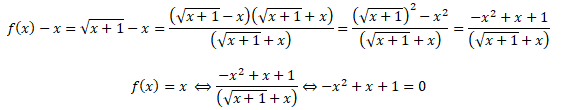
Discriminant D = 12+4 = 5.
On retient la racine positive : (1+5½) / 2.
Partie B.
On considère la suite (un) définie par u0 = 5 et pour tout entier naturel n, par un+1 = f (un) où f est la fonction étudiée dans la partie A.
On admet que la suite de terme général un est bien définie pour tout entier naturel n.
1. Démontrer par récurrence que pour tout entier naturel n, on a 1 < un+1 <un.
Initialisation : u0 = 5; u1 = f(u0) =f(5) = (5+1)½ = 6½~2,45. 1 < u0+1 <u0 est vérifiée.
Hérédité : 1 < un+1 <un est supposée vraie.
f étant croissante : f(1) < f(un+1) < f(un).
2½< un+2 < un+1.
2½ étant supérieur à 1 : 1< un+2 < un+1.
La propriété est vérifiée au rang n+1.
Conclusion : la propriété est vraie au rang 0 et héréditaire, elle est donc vraie pour tout entier n.
2. En déduire que la suite (un) converge.
un+1 < un la suite est donc décroissante.
1 < un la suite est minorée par 1.
La suite étant décroissante et minorée, elle converge.
3. Démontrer que la suite (un) converge vers l=(1+5½) / 2.
D'après le théorème du point fixe, la limite est solution de l'équation f(x) = x dand l'intervalle [0 ; +oo[.
D'après la question3, la solution de cette équation est (1+5½) / 2.
Cette valeur étant supérieure à 1 et inférieure à u0, la suite converge vers (1+5½) / 2.
4. On considère le script Python ci-dessous :
from math import *
def seuil(n):
u=5
i=0
5ℓ =(1 + sqrt(5))/2
while abs(u-ℓ)>=10**(-n):
u=sqrt(u+1)
i=i+1
return(i).
a. Donner la valeur renvoyée par seuil (2).
seuil(2) renvoye l'indice du premier terme qui est à moins d'un centième de la limite l.
La calculatrice renvoye la valeur 5.
b. La valeur renvoyée par seuil (4) est 9.
Interpréter cette valeur dans le contexte de l’exercice.
C'est le premier terme de la suite qui est une valeur approchée de l à 10-4 près.
|
ane.
|
|
|