Acoustique d'une salle de spectacle, bac centres étrangers 2024

L’étude de l’acoustique d’une salle de spectacle nécessite notamment de prendre en compte les différents phénomènes liés à la propagation des ondes sonores : interférences, diffraction, atténuation.
Données :
− fréquences f audibles par l’oreille humaine : 20 Hz < f < 20 kHz ;
− vitesse de propagation dans l’air d’une onde sonore ou ultrasonore v = 343 m·s^-1 à 20 °C ;
− largeur de la porte de l’auditorium : a = 1,0 m.
Une salle de concert est généralement un espace clos.
Cependant, si sa porte est ouverte, le concert peut être entendu par une personne située à l’extérieur, même lorsque l'orchestre reste hors de sa vue.
En se plaçant devant la porte, cette personne peut entendre toute la gamme des sons. Cependant, si elle se place sur le côté, elle entend surtout les sons graves, et très peu les sons aigus.
Dans les questions suivantes on s’intéresse au phénomène de diffraction des ondes sonores.
On peut modéliser la situation décrite dans le document par le schéma suivant :

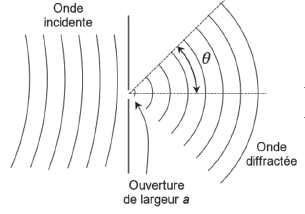
On rappelle que l’expression de l’angle d’ouverture q associé au phénomène de diffraction en
fonction de la largeur de l’ouverture, notée a, et de la longueur d’onde l de la source est : sin q = l /a.
Q1. Montrer que l’expression de l’angle d’ouverture q en fonction de la largeur de l’ouverture a,
de la fréquence f de l’onde émise par la source et de la vitesse de propagation v de l’onde est :
θ = arcsin ( v / (f a).
sin q = l / a et l = v / f ; sin q =v / (f a) ; θ = arcsin ( v / (f a).
Deux ondes sonores sont produites par un orchestre. Elles sont caractérisées par deux fréquences
typiques : f₁ = 440 Hz et f₂ = 4×f₁ = 1 760 Hz.
Q2. Calculer les valeurs de q₁ et q₂ correspondant respectivement aux valeurs de fréquences f₁et f₂.
q₁ = arcsin( 343 / (440 x 1,0) =arcsin(0,78) = 51°.
q₂ = arcsin( 343 / (1760 x 1,0) =arcsin(0,195) = 11°.
Q3. Schématiser de façon cohérente la situation, en représentant les angles d’ouverture correspondants q₁ et q₂ après passage du son par l’ouverture. Commenter la phrase : « Cependant, si elle se place sur le côté, elle entend surtout les sons graves, et très peu les sons aigus ».

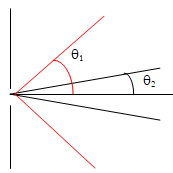
q₂ ( sons aigus) << q₁ (sons graves) : si la personne se place sur le côté, elle entend surtout les sons graves, et très peu les sons aigus »
Dans les questions suivantes, on s’intéresse au phénomène d’interférences susceptible d’intervenir à la suite des réflexions d’une onde sonore dans une salle de spectacle. On transpose l’étude dans le domaine des ondes ultrasonores.
On utilise le dispositif ci-dessous dans lequel les deux émetteurs d’ultrasons sont reliés à un même générateur.
La distance latérale entre les deux émetteurs E₁ et E₂ a pour valeur e = 15 cm. La distance commune entre les émetteurs et l’axe (Ox) sur lequel se déplace le récepteur a pour valeur D = 50 cm.

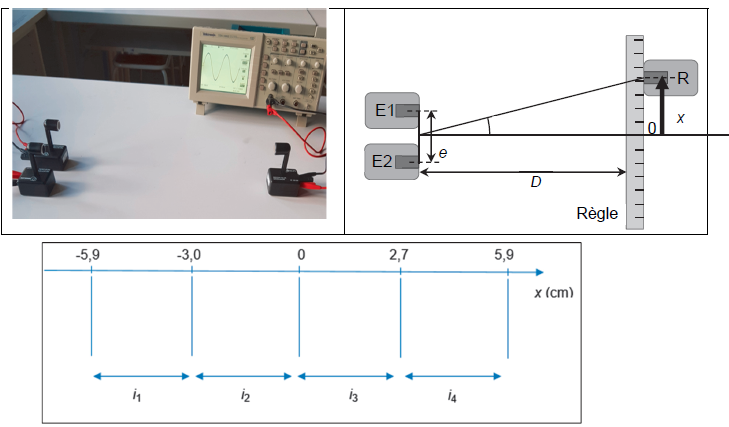
Q4. Relever les valeurs des interfranges mesurées expérimentalement et calculer leur moyenne i.
i =(2,9 +3 +2,7 +3,2) / 4 =2,95 cm.
On admet que la différence des distances entre chaque émetteur et le récepteur est :
E₂R – E₁R = e·x / D
Q5. Établir la condition d’interférences constructives portant sur x ; on pourra utiliser la notation n pour l’entier relatif qui pourrait être utile.
E₂R – E₁R = n l = e·x / D.
x = n l D / e.
On admet que la distance entre deux maxima d’amplitude consécutifs (interfrange) s’écrit i = l·D / e avec l la longueur d’onde des deux ondes incidentes.
Q6. Déduire la valeur de la fréquence des signaux délivrés par les émetteurs ; commenter.
l = i e / D = 2,95 10^-2 x0,15 / 0,50 =8,85 10^-3 m.
f = v / l = 343 / (8,85 10^-3) =3,9 10⁴ Hz = 39 kHz, valeur supérieure à 20 kHz, domaine des ultrasons..