La
tour de la terreur,
bac Centres étrangers 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Surplombant un célèbre parc d’attraction du haut de ses treize étages, La Tour de la Terreur entraîne une cabine avec ses
passagers dans une chute vertigineuse de plusieurs dizaines de mètres.
L’objet de cette étude est de d’étudier certaines caractéristiques du fonctionnement de l’attraction.
Le système étudié est l’ensemble {cabine + passagers}, de masse m ; le centre de masse M du système, d’altitude z, est
situé à près de 1 m au-dessus du bas de la cabine.
Après une phase ascendante durant laquelle le centre de masse de la
cabine monte jusqu’à 40,0 m au-dessus du sol, le mouvement de la cabine
se décompose en deux phases :
- une première phase qu’on modélise par une chute libre de 40,0 m à 8,0 m, d’une durée d’environ deux secondes ;
- une deuxième phase de freinage pour stopper la cabine, d’une durée d’environ une seconde.
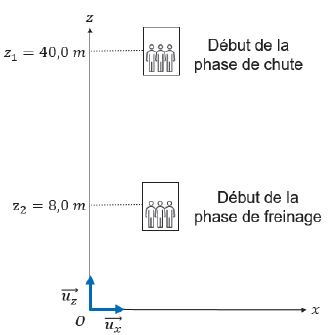
La vitesse v de la cabine est nulle au début de la première phase ;
Vitesse maximale mesurée de la cabine : vmax = 63 km·h-1 ou 63 / 3,6 =17,5 m /s.
Masse de la cabine avec une vingtaine de passagers : m = 8,5 x 103 kg ;
Le nombre de g représente une valeur d’accélération multiple de g. Par exemple, une accélération de 4 g vaut 4 × 9,8 m·s-2 = 39 m·s-2. Elle est dangereuse lorsqu’elle est subie pendant une durée supérieure à 1 s.
Q1. Rappeler l’hypothèse principale du modèle de la chute libre.
Le système étudié n'est soumis qu'à son poids.
Q2. Rappeler, pour
le système étudié, les expressions de l’énergie cinétique Ec, de
l’énergie potentielle de pesanteur Epp, supposée nulle en z = 0, et de
l’énergie mécanique Em.
Ec = ½mv2 ; Epp = mg z ; Em = ½mv2 + mgz.
Q3. Par une
approche énergétique, montrer que dans ce modèle de la chute libre, à
la fin de la première phase, la cabine devrait avoir une vitesse de 25
m·s-1.
Energie mécanique initiale : mg z1 ; énergie mécanique finale : mgz2 +½mv2.
Conservation de l'énergie mécanique : mg z1=mgz2 +½mv2.
v2 = 2g(z1-z2) =2 *9,8 (40-8)=627,2 ; v =25 m/s.
Q4.
Compte-tenu de la valeur de la vitesse maximale mesurée de la cabine,
interroger la pertinence du modèle de la chute libre pour l’étude de la
première phase du mouvement de la cabine.
Le modèle de la chute libre n'est pas pertinent, la vitesse en fin de première phase n'est que de 17,5 m /s.
Dans
les questions suivantes on s’intéresse à la deuxième phase du mouvement
: le freinage de la cabine. Durant cette phase, un système constitué de
six freins à tambour exerce sur la cabine, par l’intermédiaire d’un
câble, une force de freinage Fque l’on suppose constante, de valeur F =
2,7 × 105 N. Les forces de frottements de l’air sont supposées négligeables ici
devant cette force de freinage.
Q5. Représenter sur un schéma les deux forces qui s’exercent sur la cabine lors de la phase de freinage.
Force de freinage F, verticale, vers le haut, valeur 2,7 105 N.
Poids, verticale vers le bas, valeur mg = 8,5 103 x9,8 =8,3 104 N.
Q6. Déterminer
l’expression du vecteur accélération a de la cabine sur les directions
(Ox) et (Oz) en fonction de F, g et m et des vecteurs unitaires.
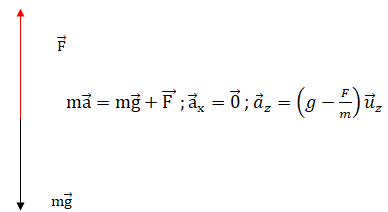
La valeur de l’accélération subie par la cabine et ses passagers durant la phase de freinage est environ a = 22 m·s-2, soit a = 2,2 g.
Q7. Discuter de la
dangerosité de cette attraction sur le corps humain étant donné
l’accélération subie et la durée approximative de la phase de freinage.
2,2 g < 4 g et la phase de freinage dure environ 1 s : il n'y a pas de danger pour le corps humain.
Lors de la deuxième phase, la position du centre de masse de la cabine vérifie la loi horaire suivante :
z(t)=½at2-vmaxt+z2.
avec a = 22 m·s-2, vmax = 18 m·s-1 et z2 = 8,0 m. L’origine des temps est prise au début de la deuxième phase.
Q8. Montrer que la cabine s’arrête au bout de 0,8 s environ.
1 =11 t2-18t+8 ; 11 t2-18t+7=0.
Discriminant D = 182-4*11*7=16 ; on retient la racine positive : t = (18-4) / 22 ~0,8 s.
|