L'homme canon, bac Centres étrangers 2024 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . .. . .. .. ...... ... Le système ( artiste + équipement, assimilé à un point matériel G, de masse m = 80 kg n'est soumis qu'à son poids, l'action de l'air étant négligée. Initialement l'homme démarre son vol et occupe la position G0. Après le vol, le système retrouve le contact avec le filet situé à une hauteur h = 8,0 m au dessus du sol. 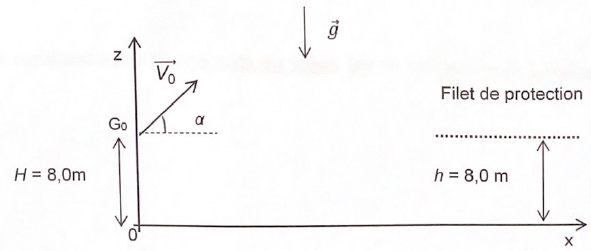a = 45° ; V0 = 31 m/s. Etude énergétique. 1. Exprimer l'énergie mécanique du système à t = 0. E = ½mV02 + mgH. 2. Déterminer la vitesse du système à l'arrivée dans le filet. E = ½mv2 + mgh. Conservation de l'énergie mécanique. ½mV02 + mgH= ½mv2 + mgh. Or H = h, en conséquence V = V0. 3. Représenter l'évolution des énergies cinétiques, potentielle de pesanteur et mécanique au cours du vol. 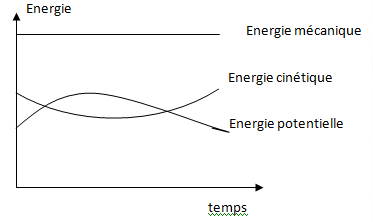Etude du mouvement après le lancer. 4.Exprimer les coordonnées du vecteur accélération pendant le vol. Le système n'étant soumis qu'à son poids, verticale vers le bas, valeur mg, la seconde loi de Newton conduit à : ax = 0 ; az = -g. 5. En déduire les équations horaires du mouvement. La vitesse est une primitive de l'accélération : vx = Cste =  V0 cos a. vy = -gt + V0 sin a. La position est une primitive de la vitesse et la position initiale est G0(0 ; H). x = V0 cos a t. z = -½gt2 + V0 sin a. t +H. 6. Donner la valeur de z(t) lorsque le système entre en contact avec le filet de protection. z(t) = h =H= 8 m. ... .... 7. En déduire la durée du vol et la portée. -½gt2 + V0 sin a. t +H = h ; or H = h. -½gt2 + V0 sin a. t = 0 ; -½gt + V0 sin a = 0 ; t = 2 V0 sin a / g = 2 x31 xsin45 / 9,81 =4,47 ~4,5 s. x = V0 cos a t : 31 xcos45 x4,47 ~98 m. 8. Comparer cette valeur avec la longueur homologuée 56,64 m et conclure. Ce modèle de la chute libre n'est pas valable, la portée étant bien supérieure à 56,64 m. Il faut prendre en compte les frottements sur les couches d'air. ane.

menu