Mathématiques,
bac Centres étrangers 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. 5 points.
Partie A.
On définit la fonction f sur l'intervalle [0 ; 1] par : f(x) = 0,96 x / (0,93 x+0,03).
1. Démontrer que f '(x) = 0,0288 / (0,93 x+0,03)2.
On pose u = 0,96 x ; v = 0,93x+0,03 ; u' = 0,96 ; v' = 0,93.
(u'v-v'u) / v2 =(0,96(0,93x+0,03) -0,93(0,96x) / (0,93 x+0,03)2 =0,0288 / (0,93 x+0,03)2.
2. Déterminer le sens de variation de la fonction f.
f '(x) >0 ; f(x) est strictement croissante sur [0 ; 1].
Partie B.
Lors d'une compétition rassemblant 1000 sportifs, une équipe médicale
teste tous les concurrents. On note x la proportion de sportifs dopés.
La probabilité qu'un sportif soit déclaré positif sachant qu'il est dopé est égale à 0,96.
La probabilité qu'un sportif soit déclaré positif sachant qu'il n'est pas dopé est égale à 0,03.
On note :
D l'événement " le sportif est dopé ".
T : l'événement " le test est positif".
1. Compléter l'arbre de probabilité.
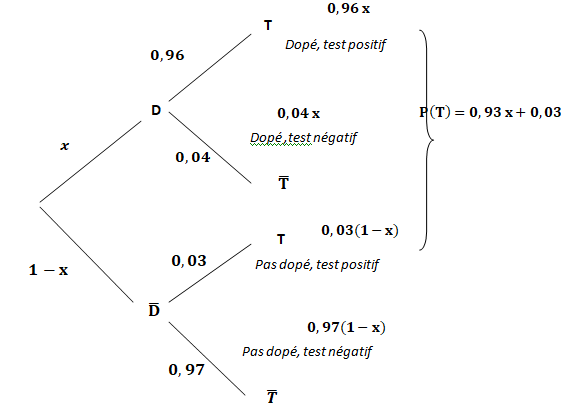
2. Déterminer en fonction de x, la probabilité qu'un sportif soit dopé et ait un test positif.
0,96 x.
3. Démontrer que P(T) = 0,93 x +0,03.
Formule des probabilités totales : P(T) = 0,96 x +0,03(1-x) =0,93 x +0,03.
4. Pour cette
question, il y a 50 sportifs dopés parmi les 1000 testés. Démontrer que
la probabilité qu'un sportif soit dopé sachant que son test est positif
est égale à f(0,05).
PT(D) =P(D n T) / (P(T)=0,96 x /(0,93x +0,03) avec x = 0,05.
f(0,05) = 0,96 x0,05 /(0,93 x0,05 +0,03) =0,048 / 0,0765 ~0,63.
5. On appelle valeur prédictive positive d'un test la probabilité que le sportif soit réellement dopé lorsque le test est positif.
a. Déterminer à partir de quelle valeur de x la valeur prédictive du test sera supérieure ou égale à 0,9.
0,96 x /(0,93x +0,03) > 0,9.
0,96 x > 0,837 x +0,027.
x > 0,22.
b. On ne test que
les sportifs les plus performants supposés être plus fréquement dopés.
Quelle est la conséquence de cette décision sur la valeur prédictive.
f(x) est strictement croissante ; x croît et en conséquence la valeur prédictive du test.
Exercice 2. 5 points.
f(x) = 2x e-x définie sur [0 ; 1].
1. Résoudre l'équation f(x) = x sur cet intervalle.
2xe-x = x ; 2e-x = 1 ; -x = ln(0,5) ; x = ln(2).
2. Démontrer que f '(x) = 2(1-x)e-x.
On pose u = 2x et v = e-x ; u' = 2 ; v' =-e-x ; u'v+v'u =2e-x-2xe-x= 2(1-x)e-x.
c. Donner le tableau de variations de la fonction f sur [0 ; 1].
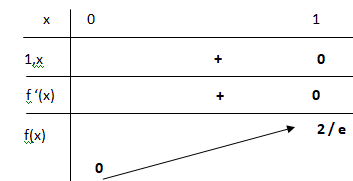
On considère la suite (un) définie par u0 = 0,1 et un+1 = f(un).
2.a. Démontrer par écurrence que 0 < un < un+1 < 1.
Initialisation : u0 = 0,1 ; u1 = f(0,1) =0,2 e-0,1 ~0,18 < 1. La propriété est vraie au rang zéro.
Hérédité. 0 < un < un+1 < 1 est supposé vraie.
f(x) étant strictement croissante de 0 à 2 /e : . f(0) < f(un) < f(un+1) < f(1)
0 < un+1 < un+2 < 1. La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est vraie pour tout entier naturel n.
b. En déduire que la suite est convergente.
La suite est croissante et bornée, donc elle converge.
3. Démontrer que la limite de la suite est ln(2).
A la limite, un = un+1 ; l = 2l exp(-l) ; 0,5 = exp(-l) ; l = ln(2).
4.a. Justifier que ln(2) -un >0
La suite est croissante et sa limite est ln(2), donc ln(2) -un >0.
b. On écrit un script qui renvoie une valeur approchée de ln(2) à 10-4 près par défaut ainsi que le nombre d'étapes pour y parvenir.
def seuil()
n=0
u =0,1
while ln(2)-u > 0,0001.
n = n+1
u = 2*u*exp(-u)
return (u,n).
c. Donner la valeur de n renvoyée par la fonction seuil.
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
9
|
10
|
11
|
12
|
u
|
0,1
|
0,18096
|
0,3020
|
0,4466
|
0,5714
|
0,6454
|
0,6769
|
0,6880
|
0,69155
|
0,6927
|
0,693
|
0,6931
|
ln(2)-u
|
0,5931
|
0,51218
|
0,3911
|
0,2466
|
0,1217
|
0,04474
|
0,01618
|
0,0051
|
0,0016
|
0,00049
|
0,00015
|
4,6 10-5
|
..
|
...
|
....
|
Exercice 3. 5 points.
On considère l'équation différentielle (E0) : y' = y.
1. Démontrer que l'unique fonction constante solution de (E0) est la fonction nulle.
y = Cste ; y' = 0 ; Cste = 0.
2. Déterminer toutes les solution de (E0).
y = A exp(x) avec A une constante réelle.
On considère l'équation différentielle (E) : y' = y -cos(x)-3 sin(x).
3. Démontrer que la fonction h(x) = 2 cos(x) +sin(x) est solution de (E).
h'(x) = -2 sin(x) +cos(x).
Repport dans (E) : -2 sin(x) + cos(x) = 2 cos(x) +sin(x)-cos(x) -3 sin(x) =cos(x)-2 sin(x) est vérifié pour tout x.
4. Démontrer que " f est solution de (E) " est équivalent à (f-h) est solution de (E0).
f est solution de (E) : f ' = f -cos(x)-3 sin(x).
f-h = f-2 cos(x) -sin(x) ;
f ' - h ' = f '+2 sin(x) -cos(x)= f -cos(x) -3 sin(x)+2 sin(x)- cos(x) =f -2 cos(x)-sin(x)= f-h..
Repport dans (E0) : f ' -h' =f-h est bien vérifié.
5. En déduire toutes les solution de (E).
solution générale de (E0) + solution particulière de (E).
y =A exp(x) + 2 cos(x) +sin(x).
6. Déterminer l'unique solution g de (E) telle que g(0) = 0.
0 = A+2 ; A = -2.
y = -2exp(x)+2 cos(x) +sin(x).
7. Calculer :
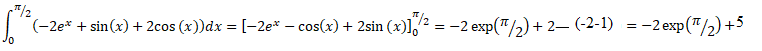
Exercice 4. 5 points.
Soient les points A(-2 ; 0 ; 2) ; B(-1; 3 ; 0) ; C(1 ; -1 ; 2) et D(0 ; 0 ; 3).
Représentation paramétrique de la droite (D1) :
x=t ; y =3t ; z = 3+5t avec t réel.
Représentation paramétrique de la droite (D2) :
x = 1+3s ; y = -1-5s ; z = 2-6s avec s rel.
1. Démontrer que les points A, B et C ne sont pas alignés.
2. a Démontrer que le vecteur n(1 ; 3 ; 5) est orthogonal au plan (ABC).
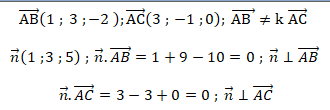
b. Justifier qu'une équation du plan (ABC) est : x+3y+5z-8=0.
x+3y+5z+d=0
A (-2 ; 0 ; 2) appartient à ce plan :
-2+0+10+d = 0 ; d = -8.
c. En déduire que les points A, B, C et D ne sont pas coplanaires.
Si D appartient au plan (ABC), les coordonnées de D doivent vérifier l'équation du plan.
0 +0 +5*3-8 = 7 diffère de zéro.
D n'appartient pas au plan(ABC).
3.a Justifier que la droite (D1) est la hauteur du tétraèdre ABCD issue de D.
Equation paramétrique de la droite (D1) :
x=t ; y=3t ; z = 3+5t.
Pour t = 0 : x =0 ; y = 0 ; z =3 ; il s'agit des coordonnées du point D.
Donc D appartient à la droite (D1).
Coordonnées d'un vecteur directeur de la droite (D1) : (1 ; 3 ; 5), c'est à dire celles du vecteur n orthogonal au plan (ABC).
(D1) est une droite issue de D et orthogonal au plan (ABC).
(D1) est la hauteur du tétraèdre ABCD issue de D.
b. Démontrer que les droite (D1) et (D2) sont sécantes et déterminer les coordonnées de leur point d'intersection.
Si les droites sont sécantes en M(x ; y; z), les coordonnées du point M vérifient :
t = 1+3s ; 3t = -1-5s ; 2-6s=3+5t
3+9s=-1-5s soit 4= -14s ; s=-2 / 7. Par suite t = 1 / 7.
2 +12 / 7=3+5 / 7 soit 26 / 7 =26 /7 est vérifié.
Le système admet une solution unique, donc les droites (D1) et (D2) sont sécantes.
Coordonnées de leur point d'intersection M :
On remplace t par 1 /7 dans la représentation paramétrique de (D1) :( 1 / 7 ; 3 / 7 ; 26 /7).
4.a. Déterminer les coordonnées du projeté orthogonal H du point D sur le plan (ABC).
Les coordonnées de H vérifient l'équation cartésienne du plan(ABC) et la représentation paramétrique de la droite (D1).
t + 3 x(3t)+5 x(3+5t)-8 = 0.
35 t = -7 ; t = -1 / 5.
On remplace t par -1/5 dans l'équation paramétrique de (D1) :
x = -1 /5 ; y = -3 / 5 ; z = 2.
b. Calculer la distance du point D au plan (ABC).
H étant le projeté orthogonal du point D sur le plan (ABC) :
DH2 = (-1/5-0)2 +(-3/5-0)2 +(2-3)2 = 1/25 +9/25+1=35/25=7/5.
DH ~1,18.
|
ane.
|
|
|