Cinétique,
acide base, dipôle RL, pendule élastique, sons,
Bac sciences Tunisie 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Chimie.
Cinétique
d'oxydation des ions iodures par les ions peroxodisulfate.
2I-aq + S2O82-aq
= I2aq + 2SO42-aq. (1)
KI : volume V1
= 50 mL ; concentration C1.
K2S2O8 : V2 = 50 mL,
concentration C2.
A différentes dates on prélève un volume VP de ce mélange ;
dilution avec de l'eau glacée et dosage du diiode.
1. Indiquer le rôle de l'eau glacée et celui de l'empois d'amidon.
En diluant le prélèvement avec de
l'eau glacée avant de procéder au dosage, on réalise un blocage
cinétique.
L'empois d'amidon est un indicateur permettant de repérer l'équivalence.
2. Montrer que [I2] = 0,5 C0VE / VP.
Concentration du
diiode à la date t :
Réaction de dosage : I2aq + 2S2O32-aq
= 2I-aq + 2S4O62-aq.
Thiosulfate de sodium : concentration C0.=10-3
mol / L ; volume ajouté à l'équivalence VE.
Volume de la prise d'essai : VP.
A l'équivalence n( I2aq) = 0,5 n(S2O32-aq) ;
[I2] VP = 0,5 C0VE ; [I2] = 0,5 C0VE / VP.
3. Exprimer à la date t la concentration en ion iodure dans le mélange.
Quantité de matière initiale d'ion iodure dans la prise d'essai : VPC1.
Quantité de matière de diiode formé en (1) et titré : 0,5 VEC0.
Quantité de matière d'ion iodure ayant réagi
avec l'ion peroxodisulfate : 2 n(I2 ) =C0VE .
Quantité de matière d'ion iodure
restant dans la prise d'essai : VPC1 -C0VE
.
[I-] =C1 -C0VE / VP.
4. Exploiter les courbes suivantes et en déduire C1, VP, C2.
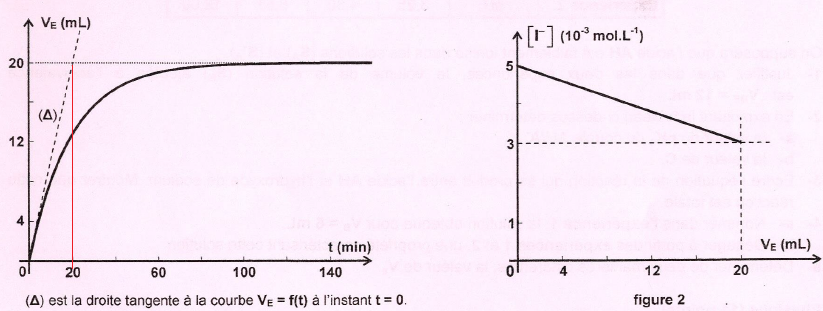
D'après la figure
2 : C1 =
5 10-3 mol / L.
C0 / VP = (5-3) 10-3 / (20 10-3)
=0,1.
VP = C0 / 0,1 =0,01 L = 10 mL.
Au bout d'un temps suffisamment long, il reste des ions iodure ; ceux
ci-sont donc en excès par rapport aux ions peroxodisulfate.
n(I-) restant = 3 10-3 mol / L.
n(I-) initial= 5 10-3 mol / L.
n(I-)
réagissant en (1) = 2 10-3 mol / L.
n( S2O82-aq) initial = 0,5 n(I-)
réagissant en (1) =10-3 mol / L.
C2 =
n( S2O82-aq) initial / V2
=10-3 / 0,050 =0,02 mol / L.
5. Exprimer la vitese volumique de la réaction. Déterminer cette vitesse à t = 0.
Vitesse volumique
de la réaction (1) :
v(t) = d[I2] /dt ; [I2] = 0,5 C0VE / VP.
v(t) = 0,5 C0 / VP dVE /dt.
A t =0, coefficient directeur de la tangente à la courbe VE
= f(t) =20 / 20 = 1 mL / min.
Expérience 2.
mêmes conditions que précédemment et on ajoute au mélange initial V =
50 mL d'eaau distillée prise à la même température que le mélange.
La concentration est un facteur cinétique. Si la concentration des
réactifs diminue, la vitesse de la réaction diminue.
Concentration finale des ions
iodure :
Expérience 1 : volume du mélange = 100 mL. n(I-) restant =
3 10-3 mol / L.
Exprience 2 : volume du
mélange =150 mL.
n(I-) restant =
3 10-3 x100 / 150 =2 10-3 mol / L.
Titrage acide faible base forte.
Le monoacide
faible HA et la soude ont la même concentration C.
Expérience 1
: titrage de VA = 12 mL de cet acide sans ajout d'eau
distillée.
Expérience
2 : titrage de VA = 12 mL de cet acide avec ajout
d'un volume VE d'eau distillée.
On suit l'évolution du pH.
|
VB(mL)
|
0
|
6
|
12
|
20
|
expérience
1
|
pH
|
2,90
|
4,80
|
8,75
|
12,40
|
expérience
2
|
pH
|
3,25
|
4,80
|
8,51
|
12,00
|
1. Montrer que VBE = 12 mL.
Un saut de pH
est observé pour VBE
= 12 mL.
A
l'équivalence : CVA = CVéqui soit VA
= Véqui ; le volume de soude ajouté à l'équivalence est donc Véqui
= 12 mL.
2. Calculer C et le pKa du couple acide / base.
A la demi équivalence le pH est égal au pKa du couple acide base soit
pKa = 4,80.
Calcul
de C.
pH = pKa + log ([A-] / [AH]).
2,90 = 4,80 + log ([A-]1
/ [AH]1).
Expérience 1 : log ([A-]1
/ [AH]1) = -1,9 ; [A-]1 / [AH]1=0,0126.
La solution
est électriquement neutre : [A-]1 +[HO-] = [H3O+].
A pH =2,90, [HO-] est négligeable ; [A-]1 ~ [H3O+]~10-2,9
~1,26 10-3 mol / L.
[AH]1=[A-]1 /0,0126 =0,10
mol / L.
C1 = 0,10 +1,26 10-3 ~0,10 mol / L.
Expérience
2 :
3,25 = 4,80 +
log ([A-]2
/ [AH]2).
log ([A-]2
/ [AH]2) = -1,55 ; [A-]2 / [AH]2=0,0282.
La solution est électriquement neutre : [A-]2 +[HO-] = [H3O+].
A pH =3,25, [HO-] est négligeable ; [A-]2 ~ [H3O+]~10-3,25
~5,6 10-4 mol / L.
[AH]2=[A-]2 /0,0282 =0,02
mol / L.
C2
= [A-]2 + [AH]2
=0,02 mol / L.
3. Montrer que AH + HO- --> A-+H2O
est totale.
K = [A-] /( [AH][HO-])= [A-]
[H3O+]/ ([AH][HO-][H3O+])
= Ka / Ke = 10-4,8 / 10-14 =1,6 109.
K est grand, la réaction est donc totale.
4. Nommer dans l'expérience 1 la solution obtenue pour VB = 6mL. En donner une propriété.
Solution tampon pour VB = 6 mL car à la demi-équivalence [A-]
= [AH].
Une solution tampon modère la variation du pH lors de l'ajout modéré
d'un acide ou d'une bas forte, lors d'une dilution modérée.
5. Calculer VE.
Facteur de dilution : C1/C2 =0,10 / 0,02 = 5.
(VA+VE) / VA
= 5 ; VA+VE=
5 VA
; VE =4 x12 = 48 mL.
|
...
|
....
|
Physique.
Dipôle RL.
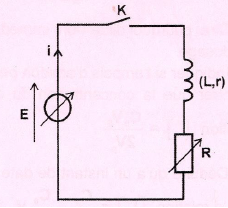
Expérience 1
: E = 6 V ; R = 85 ohms.
1. Nommer le phénomène physique mis en évidence.
L'établissement
d'un courant continu dans un dipôle RL n'est pas instantané :
apparition d'un courant induit qui s'oppose à l'établissement du
courant. La bobine stocke de l'énergie.
2. Déterminer l'intensité I1 en régime permanent et la constante de temps du circuit. En déduire r et L.
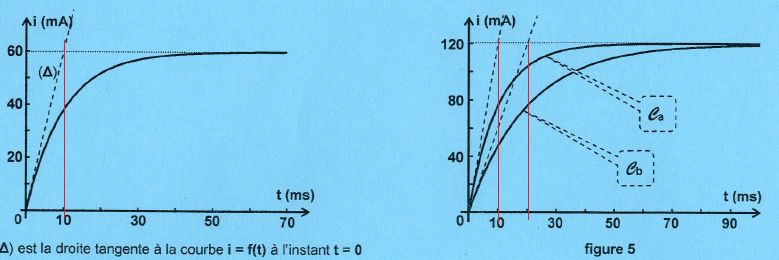
En régime permanent I1 = 60 mA.
Constante de temps t
= 10 ms = 0,01 s. ( figure 4 : abscisse de l'intersection de la
tangente à l'origine avec l'asymptote horizontale).
En
régime permanent : I = E /(r+R).
I(r+R)=E ; r+R = E/ I ; r =E/ I-R=6 / 0,06 -85 =15 ohms.
t = L
/(R+r)= 0,01.
L = 0,01 x(85+15) =1 H.
Expériences 2 et 3.
( figure 5).
Expérience 2
: R = 85 ohms ; E est modifiée.
1. Déterminer les nouvelles valeurs de E et R.
La constante de temps reste inchangée ( courbe Ca)
En régime permanent I = E /(R+r) =0,12 A
E = 0,12 x(85 +15) =12 V.
Exprrience 3
: E = 6 V et R est modifiée.
La constante de temps change ( courbe Cb) et vaut 20 ms =0,02 s.
0,02 = 1 /(R+15) ; R+15 = 1/0,02 =50 ; R = 35 ohms.
Pendule élastique.
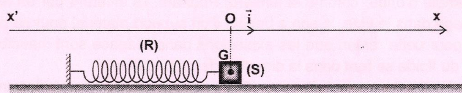
m : masse du solide S ; k : raideur du ressort. Les frottements sont négligés.
On écarte le solide jusqu'à un point A( xA =1 cm) et on l'abandonne avec une vitesse v0, en sens contraire de l'axe.
Les oscillations de G sont régient par l'équation différentielle : d2x/dt2 + k /m x = 0.
1. Exprimer la période propre en fonction de k et m.
Expression de la période propre T0.
w2 = k / m ; T0 = 2 p / w = 2 p (m/k)½.
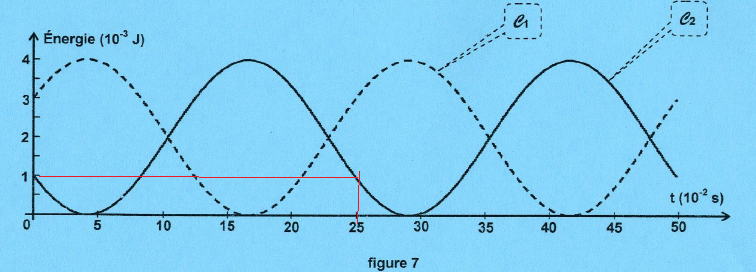
2. Déterminer k et m.
A t0+, l'énergie potentielle élastique ( courbe C2) diminue et l'énergie cinétique augmente.
Energie potentielle initiale : ½kxA2 =0,5 k x0,012 = 5 10-5 k = 10-3..
k =20 N m-1.
La période de l'énergie potentielle est T0 2=0,25 s2.
T0 = 0,5 s.
T0 = 2 p (m/k)½=0,5 ; (m / k)½ = 0,5 / 6,28 =0,0796.
m = 0,07962 x20=0,127 kg.
3. Déterminer la valeur de la phase initiale.
Ec(t=0) = ½mv02 ; v02 = 2 Ec(t=0) / m = 2 x3 10-3 / 0,127=0,0472. v0 =0,217 m /s.
Ep max = ½kX2max = 4 10-3 J ; X2max = 8 10-3 / 20=4 10-4 ; Xmax = 0,02 = 2 cm.
x(t) = Xmax sin(2p / T0 t + f).
x(t=0) =0,01 =0,02 sin( f )
0,5 = sin( f ) ; f =30° = p / 6 rad.
Expérience 2.
Le solide est soumis à une force de frottement de norme f = h v.
On enregistre pour trois valeurs de h ( 0,15 kg /s ; 0,4 kg/s ; 4 kg/s) l'évolution temporelle de x(t).
1. Attribuer à chaque courbe la valeur correspondante du coefficient de frottement.
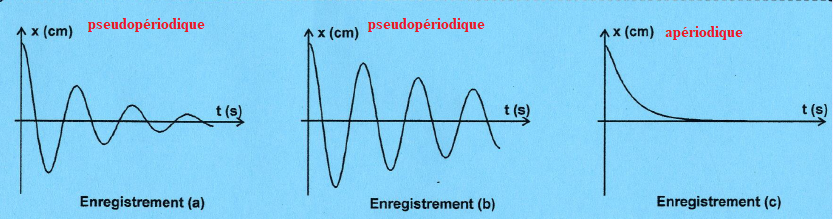
(b) : h = 0,15 kg /s ; peu de diminution d'énergie de l'oscillateur.
(a) : h = 0,4 kg /s ; diminution plus importante de l'énergie de l'oscillateur.
(c) : h =4 kg/s ; très grande diminution de l'énergie de l'oscillateur.
Le son... une onde qui se propage.
La
propagation du son s'effectue sans transport de matière : " l'air vibre
mais en moyenne reste sur place, alors que le mouvement se propage de
proche en proche".
Le son est une onde mécanique : " le son est un exemple d'onde....il a besoin d'un support matériel pour se propager".
Le son se propage comme une onde longitudinale : " les mouvements oscillants se font dans la direction de propagation".
Dans l'espace règne le vide. Le son a besoin d'un milieu matériel
pour se propager. Les explosions dans l'espace sont donc inaudibles.
La célérité du son dépend de la nature du milieu dans lequel l'onde se propage et de la température.
Dans l'air : N = 1000 Hz ; célérité 340 m/s à 20°C.
Longueur d'onde = célérité / fréquence = 340 / 1000 = 0,34 m.
Dans l'eau : N = 1000 Hz ; célérité 1480 m/s à 20°C.
Longueur d'onde = célérité / fréquence = 1480 / 1000 = 1,48 m.
Un son ne peut donc pas être caractérisé par sa longueur d'onde, mais par sa fréquence.
|
|
|
|