Mathématiques,
bac Asie 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. 5,5
points.
Partie A.
On considère la fonction f définie sur ]0 ; +∞[ par f (x) = x2 −x ln(x).
On admet que f est deux fois dérivable sur ]0 ; +∞[.
On note f ′ la fonction dérivée de la fonction f et f ′′ la fonction dérivée de la fonction f ′.
Partie A : Étude de la fonction f
1. Déterminer les limites de la fonction f en 0 et en +∞.
En zéro : x2 tend vers zéro ; d'après la ppropriété des croissances comparée x ln(x) tend vers zéro.
Somme des limites : f(x) tend vers zéro.
En +oo : f(x) = x2 (1-ln(x) /x).
Par croissance compérée ln(x) / x tend vers zéro ; 1-ln(x) / x tend vers 1.
x2 tend vers +oo ; par limite du produit, f(x) tend vers +oo.
2. Pour tout réel x strictement positif, calculer f ′(x).
Dérivée de x ln(x) : u = x ; v = ln(x) ; u' =1 ; v' = 1 /x ; u'v+v'u = ln(x)+1
f '(x) =2 x-ln(x) -1.
3. Montrer que pour tout réel x strictement positif :
f ′′(x) =(2x −1) /x.
.f "(x) = 2 -1 /x = (2x-1) / x.
4. Étudier les variations de la fonction f ′ sur ]0 ; +∞[, puis dresser le tableau des variations de la fonction f ′ sur ]0 ; +∞[.
On veillera à faire apparaître la valeur exacte de l’extremum de la fonction f ′ sur ]0 ; +∞[.
Les limites de la fonction f ′ aux bornes de l’intervalle de définition ne sont pas attendues.
2x-1 >0 si x > 0,5.
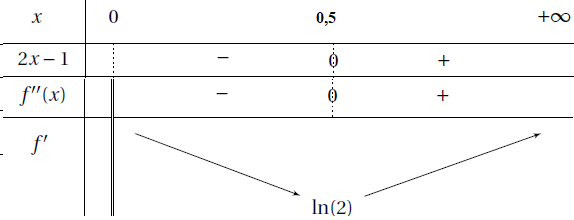
5. Montrer que la fonction f est strictement croissante sur ]0 ; +∞[.
Sur cet intervalle, le minimum de f '(x) est ln(2) >0. f '(x) >0 et f(x) est strictement croissante.
Partie B : Étude d’une fonction auxiliaire pour la résolution de l’équation f (x) = x
On considère dans cette partie la fonction g définie sur ]0 ; +∞[ par g(x) = x −ln(x).
On admet que la fonction g est dérivable sur ]0 ; +∞[, on note g′ sa dérivée.
1. Pour tout réel strictement positif, calculer g′(x), puis dresser le tableau des variations de la fonction g.
Les limites de la fonction g aux bornes de l’intervalle de définition ne sont pas attendues.
g '(x) = 1-1 /x = (1-x) / x.
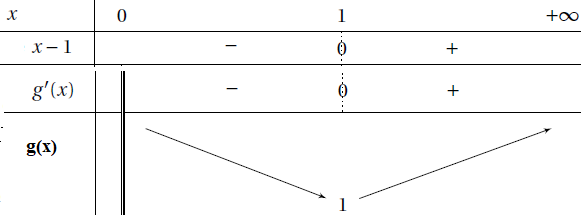
2. On admet que 1 est l’unique solution de l’équation g(x) = 1.
Résoudre, sur l’intervalle ]0 ; +∞[, l’équation f (x) = x.
f(x) = x ; x = x2-x ln(x). ; 0 = x( x-1-ln(x). x >0 donc différent de zéro.
x-1-ln(x) =0 ; x-ln(x) = 1 ; g(x) = 1 soit x = 1.
Partie C : Étude d’une suite récurrente
On considère la suite (un) définie par u0 =0,5 et pour tout entier naturel n,
un+1 = f (un) = u2n −un ln(un) .
1. Montrer par récurrence que pour tout entier naturel n : 0,5 < un < un+1 < 1.
Initialisation : u1 = f(u0) = f(0,5) =0,52-0,5 ln(0,5) =0,25 +0,5 ln(2) ~0,597.
La propriété est vraie pour n =0.
Hérédité : 0,5 < un < un+1 < 1 est supposée vraie.
f étant strictement croissante : f(0,5) < f(un) < f(un+1) < f(1).
f(0,5) < un+1) < un+12) < 1. or f(0,5) ~0,60 > 0,5.
0,5< un+1 < un+12 < 1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n.
2. Justifier que la suite (un) converge.
un < un+1 : la suite est croissante.
La suite est bornée par 0,5 et par 1.
La suite étant croissante et majorée, donc elle converge. Sa limite vérifie 0,5 < l < 1.
On appelle l la limite de la suite (un) et on admet que l vérifie l’égalité f (l) = l.
3. Déterminer la valeur de l.
D'après le théorème du point fixe, la limite est solution de l'équation f(x) = x dans l'intervalle ]0 ; +oo[.
Cette équation n'a qu'une solution 1 ( question2 Partie B)
La suite (un) converge vers 1.
EXERCICE 2 5,5 points
Léa
passe une bonne partie de ses journées à jouer à un jeu vidéo et
s’intéresse aux chances de victoire de ses prochaines parties.
Elle estime que si elle vient de gagner une partie, elle gagne la suivante dans 70% des cas.
Mais si elle vient de subir une défaite, d’après elle, la probabilité qu’elle gagne la suivante est de 0,2.
De plus, elle pense avoir autant de chance de gagner la première partie que de la perdre.
On s’appuiera sur les affirmations de Léa pour répondre aux questions de cet exercice.
Pour tout entier naturel n non nul, on définit les évènements suivants :
• Gn : « Léa gagne la n-ième partie de la journée »;
• Dn : « Léa perd la n-ième partie de la journée ».
Pour tout entier naturel n non nul, on note gn la probabilité de l’évènement Gn.
On a donc g1 =0,5.
1. Quelle est la valeur de la probabilité conditionnelle pG1 (D2) ?
Léa a gagné la première partie et perd la seconde : pG1 (D2) =0,2.
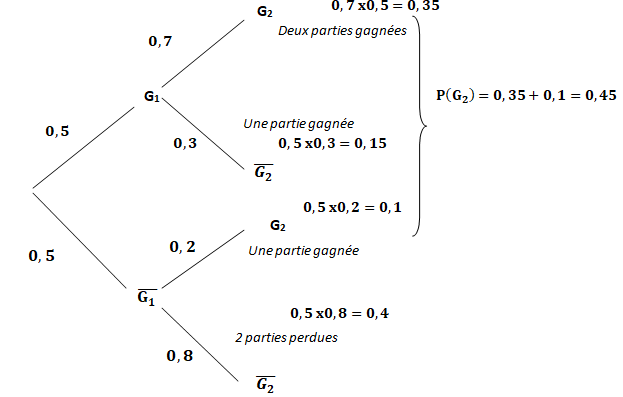
2. Recopier et
compléter l’arbre des probabilités ci-dessous qui modélise la situation
pour les deux premières parties de la journée .
3. Calculer g2.
4. Soit n un entier naturel non nul.
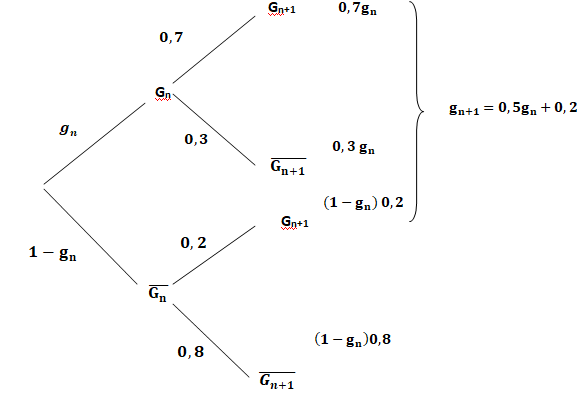
a. Recopier et
compléter l’arbre des probabilités ci-dessous qui modélise la situation
pour les n-ième et (n +1)-ième parties de la journée.
b. Justifier que pour tout entier naturel n non nul, gn+1 = 0,5gn +0,2.
5. Pour tout entier naturel n non nul, on pose vn = gn −0,4.
a. Montrer que la suite (vn) est géométrique.
On précisera son premier terme et sa raison.
vn+1 = gn+1 -0,4 =0,5 gn -0,2 =0,5(gn-0,4)=0,5 vn.
v1 =g1 −0,4 = 0,5-0,4 = 0,1. Raison q = 0,5.
b. Montrer que, pour tout entier naturel n non nul :gn =0,1×0,5n−1 +0,4.
vn = 0,1 * 0,5n-1 = gn −0,4.
gn =0,1×0,5n−1 +0,4.
6. Étudier les variations de la suite (gn).
gn+1-gn =0,1×0,5n -0,1×0,5n−1 =0,1×0,5n−1 (0,5-1) =-0,1 x0,5n.
gn+1-gn < 0 ; la suite est strictement décroissante.
7. Donner, en justifiant, la limite de la suite (gn).
Interpréter le résultat dans le contexte de l’énoncé.
-1 < 0,5 < 1; 0,5n tend vers zéro si n tend vers l'infini.
Par limite du produit et de la somme, gn tend vers 0,4.
Au bout d'un temps assez long, Léa gagnera le match dans 40 % des cas.
8. Déterminer, par le calcul, le plus petit entier n tel que gn −0,4< 0,001.
0,1×0,5n−1 < 0,001.
0,5n−1 < 0,01.
(n-1) ln(0,5) < ln(0,01) ; n-1 > ln(0,01) / ln(0,5) ; n > ln(0,01) / ln(0,5) +1 ~7,64 ; n = 8.
9. Recopier et
compléter la fonction suivante, écrite en langage Python, afin
qu’elle renvoie le plus petit rang à partir duquel les termes de la
suite(gn) sont tous inférieurs ou égaux à 0,4+e, où e est un nombre
réel strictement positif.
def seuil(e) :
g=0.5
n=1
while g >0.4+e :
g = 0.5*g+0.2
n =n+1
return (n)
|
...
|
....
|
EXERCICE
3 4 points
Pour
chacune des affirmations suivantes, indiquer si elle est vraie ou
fausse. Chaque réponse doit être justifiée.Une réponse non justifiée ne
rapporte aucun point.
1. Soit (un) une suite définie pour tout entier naturel n et vérifiant la relation suivante :
pour tout entier naturel n, 0,5 < un < (3n2 +4n +7) / (6n2+1).
Affirmation 1 en +oo, la limite de la suite est 0,5. Vrai.
Mettre n2 en facteur commun au numérateur et au dénominateur puis simplifier par n2.
(3 +4 /n +7 /n2) / 6+1/n2).
4 /n, 7 /n2 et 1 / n2 tendent vers zéro si n tend vers +oo.
(3n2 +4n +7) / (6n2+1) tend vers 3 / 6 = 0,5.
La suite (un) est encadrée par deux suites ayant pour liite 0,5 ; d'après le théorème des gendarmes la limite en +oo de un est 0,5.
2. Soit h une fonction définie et dérivable sur l’intervalle [-4; 4].
La représentation graphique Ch' de sa fonction dérivée h′ est donnée ci-dessous.
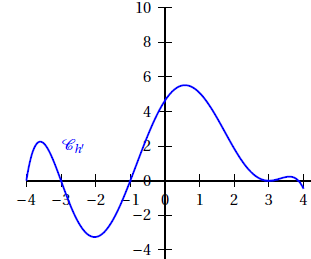
Affirmation 2 : La fonction h est convexe sur [−1 ; 3]. Faux.
Sur cet intervalle, la fonction dérivée est décroissante. La fonction h n'est pas convexe sur [−1 ; 3].
3. Le code d’un
immeuble est composé de 4 chiffres (qui peuvent être identiques) suivis
de deux lettres distinctes parmi A, B et C (exemple : 1232BA).
Affirmation 3 : Il existe 20 634 codes qui contiennent au moins un 0. Vrai.
Il y a 10 valeurs possibles pour chaque chiffre, 3 valeurs possibles
pour la première lettre et 2 valeurs possibles pour la seconde ( les
lettres doivent être distinctes)
Nombre de possibilités : 10 x 10 x10 x 10 x 3 x2 = 60 000.
Nombres de codes ne contenant pas de zéro : 9 x 9 x 9 x9 x 3 x 2 =39 366.
60 000 -39 266 = 20 634codes contenant au poins un zéro.
4. On considère la fonction f définie sur ]0 ; +∞[ par f (x) = x ln(x).
Affirmation 4 : La fonction f est une solution sur ]0 ; +∞[ de l’équation différentielle
x y′ − y = x. Vrai.
Calcul de f ' en posant u =x, v = ln(x) ; u' = 1 ; v' = 1 / x.
f '(x) = u'v+v'u = ln(x) +1.
x y' -y = x ln(x) +x -x ln(x) = x.
EXERCICE 4 5 points
Dans un repère orthonormé de l’espace, on considère le plan (P) d’équation :
(P) : 2x +2y −3z +1 = 0.
On considère les trois points A, B et C de coordonnées :
A(1; 0; 1) , B(2 ; −1 ; 1) et C(−4 ; −6 ; 5) .
Le but de cet exercice est d’étudier le rapport des aires entre un triangle et son projeté orthogonal dans un plan.
Partie A
1. Pour chacun des points A, B et C, vérifier s’il appartient au plan (P).
Si un point appartient au plan, ces coordonnées vérifient l'équation du plan (P).
2 +0 -3+1 =0, A appartient au plan (P).
4 -2-3+1 =0 ; B appartient au plan (P).
-8 -12 -15 +1 diffère de zéro ; C n'appartient pas à ce plan.
2. Montrer que le point C′(0 ; −2 ; −1) est le projeté orthogonal du point C sur le plan (P).
Coordonnées d'un vecteur orthogonal au plan (P) : 2 ; 2 ; -3.
Coordonnées du vecteur CC' : 0-(-4) ; -2-(-6) ; -1-5 soit 4 ; 4 ; -6.
Ces deux vecteurs étant colinéaires, la droite (CC') est orthogonale au plan (P).
De plus les coordonnées du point C' vérifient l'équation du plan (P).
C' est le projeté orthogonal de C sur le plan (P).
3. Déterminer une représentation paramétrique de la droite (AB).
Coordonnées du vecteur AB, vecteur unitaire de cette droite :1 ; -1 ; 0.
x = t +xA = t +1 ; y = -t+yA = -t ; z =zA =1.
4. On admet l’existence d’un unique point H vérifiant les deux conditions
H appartient à (AB) et (AB) et (HC) sont orthogonales.
Déterminer les coordonnées du point H.
H appartient à (AB) : xH = t+1 ; yH = -t ; zH =1.
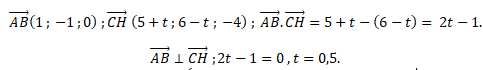
H(1,5 ; -0,5 ; 1).
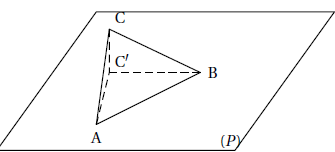
Partie B
On admet que les coordonnées du vecteur HC sont (-11 /2 ; -11 /2 ; 4)
1. Calculer la valeur exacte de HC.
HC2 =(-11 /2)2 +(-11 / 2)2 +42 =121 /4 +121 /4 +16 =306 /4 =76,5 ; HC = 76,5½.
2. Soit S l’aire du triangle ABC. Déterminer la valeur exacte de S.
H appartient à (AB) et (CH est orthogonal à (AB) :
H est la pied de la hauteur issue de C dans le triangle ABC.
Base (AB x hauteur (CH) / 2.
AB2 = 12 +(-1)2 +0 =2 ; AB = 2½.
Aire de ce triangle : (2 x76,5)½ / 2 =(153 / 2)½.
Partie C.
On admet que HC′=(17 / 2)½.
1. Déterminer la valeur de cos(CHC').
A et B appartiennent au plan (P) : la droite (AB) appartient à ce plan ; H appartenant à (AB), il appartient au plan (P).
H et C' appartiennent au plan (P).
(CC') est orthogonale à (P), donc orthogonale à toutes droites de ce plan.(CC') et C'H) sont perpendiculaires.
Le triangle CHC' est donc rectangle en C'.
cos(CHC') =C'H / CH = (17/2)½ / (153 /2)½ =(17 / 153)½ = (1/9)½ = 1 /3.
2. a. Montrer que les droites (C′H) et (AB) sont perpendiculaires.
On calcul le produit scalaire des vecteurs directeurs de deux droites.
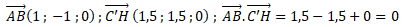
b. Calculer S′ l’aire du triangle ABC′, on donnera la valeur exacte.
S' = AB x C'H / 2 = 2½ x (17 /2)½ / 2 =17½ / 2.
c. Donner une relation entre S, S′ et cos(CHC').
cos(CHC') = C'H / CH = AB xC'H /(AB xCH) =0,5 AB xC'H /(0,5 AB xCH) =S' / S.
S' = S cos(CHC')
|
ane.
|
|
|