Mathématiques,
bac Asie 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. 5
points.
Partie A.
On considère une fonction f définie sur [0 ; +∞[, représentée par la courbe C ci-dessous.
La droite T est tangente à la courbe C au point A d’abscisse 2,5.
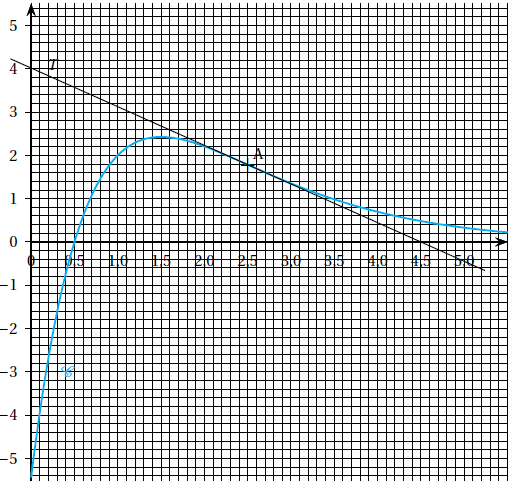
.1. Dresser, par lecture graphique, le tableau des variations de la fonction f sur l’intervalle [0; 5].

2. Que semble présenter la courbe C au point A?
La courbe semble présenter un point d'inflexion.
3. La dérivée f ′ et la dérivée seconde f ′′ de la fonction f sont représentées par les courbes ci-dessous.
Associer à chacune de ces deux fonctions la courbe qui la représente. Ce choix sera justifié.
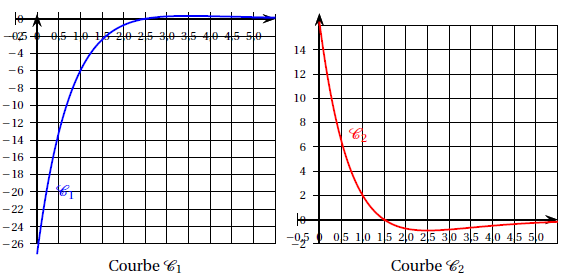
La fonction f est croissante sur l'intervalle [0 ; 1,5[ sa dérivée f ' est positive sur cet intervalle.
La fonction f est décroissante sur l'intervalle ]1,5 ; 5] sa dérivée f ' est négative sur cet intervalle.
La courbe C2 correspond à la dérivée f '.
La fonction est concave sur [0 ; 2,5[, sa dérivée seconde est négative.
La fonction est concavevexe sur ]2,5 ; 5], sa dérivée seconde est positive.
La courbe C1 correspond à la dérivée seconde.
4. La courbe suivante peut-elle être la représentation graphique sur [0 ; +∞[ d’une primitive de la fonction f ? Justifier.
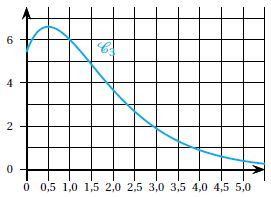
F étant une primitive de f, alors f = F' et f ' = F".
f est négative sur [0 ; 0,5[, une primitive sera décroissante sur cet intervalle.
f est positive sur ]0,5 ; 5[, un primitive sera croissante sur cet intervalle.
La fonction représentée ne convient pas.
Partie B
Dans cette partie, on considère que la fonction f , définie et deux fois dérivable sur [0 ; +∞[, est définie par
f (x) = (4x −2)e−x+1.
On notera respectivement f ′ et f ′′ la dérivée et la dérivée seconde de la fonction f .
1. Étude de la fonction f
a. Montrer que f ′(x) = (−4x +6)e−x+1.
On pose u = 4x-2 et v = e-x+1 ; u' = 4 ; v' = -e-x+1.
u'v + v' u = 4e-x+1 -(4x+2)e-x+1 =(−4x +6)e−x+1.
b.
Utiliser ce résultat pour déterminer le tableau complet des variations
de la fonction f sur [0 ; +∞[. On admet que la limite en +oo de f est
zéro.
e−x+1 >0 ; la dérivée possède le signe de -4 x+6.
x < 1,5 , f '(x) >0 et f(x) est croissante de -2e à 4e0,5.
x > 1,5, f '(x) <0, f(x) décroît de 4e0,5 à 0.
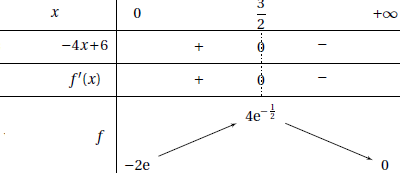
c. Étudier la convexité de la fonction f et préciser l’abscisse d’un éventuel point d’inflexion de la courbe représentative de f .
Calcul de la dérivée seconde en posant u = -4x+6 et v = e-x+1.
u' = -4 ; v' = -e-x+1 ; u'v+v'u = -4e-x+1 -(-4x+6)e-x+1 =(4x-10)e-x+1.
f " possède le signe de 4x-10.
f " >0 si x < 2,5 , f est convexe ; f "< 0 si x > 2,5 et f est concave.
2. On considère une fonction F définie sur [0 ; +∞[ par F(x) = (ax +b)e−x+1, où a et b sont deux nombres réels.
a. Déterminer les valeurs des réels a et b telles que la fonction F soit une primitive de la fonction f sur [0 ; +∞[.
Calcul de F ' en posant u = ax+b et v =e-x+1 .
u' = a ; v' = -e-x+1 ; F ' =(a-ax-b)e-x+1 = f(x).
On identifie a-b = -2 et -a = 4. Par suite a = -4 et b = -2.
b. On admet que F(x) = (−4x −2)e−x+1 est une primitive de la fonction f sur [0 ; +∞[.
En déduire la valeur exacte, puis une valeur approchée à 10−2 près, de l’intégrale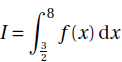
I = F(8) - F(1,5) = -34e-7 +8 e-0,5 ~4,82.
3. Une municipalité a décidé de construire une piste de trottinette freestyle.
Le profil de cette piste est donné par la courbe représentative de la fonction f sur l’intervalle [1,5 : 8].
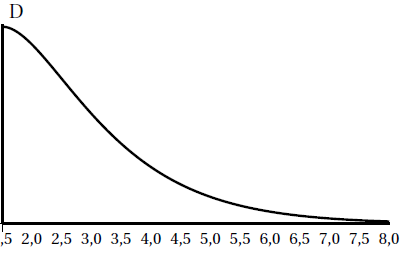
L’unité de longueur est le mètre.
a. Donner une valeur approchée au cm près de la hauteur du point de départ D.
f (1,5) = (6−2)e−0,5= 2,43 m.
b.
La municipalité a organisé un concours de graffiti pour orner le mur de
profil de la piste. L’artiste retenue prévoit de couvrir environ 75% de
la surface du mur.
Sachant qu’une bombe aérosol de 150 mL permet de couvrir une surface de 0,8 m2, déterminer le nombre de bombes qu’elle devra utiliser pour réaliser cette oeuvre.
Surface du mur 4,82 m2. Surface à couvrir : 4,82 x0,75 =3,615 m2.
3,615 / 0,8 ~4,5. Il faut 5 bombes de peinture.
EXERCICE 2 5 points
Dans l’espace muni d’un repère orthonormé d’unité 1 cm, on considère les points :
A(3 ; −1 ; 1) ; B(4 ; −1 ; 0) ; C(0 ; 3 ; 2) ; D(4 ; 3 ; −2) et S(2 ; 1 ; 4).
Dans cet exercice on souhaite montrer que SABDC est une pyramide à base
ABDC trapézoïdale de sommet S, afin de calculer son volume.
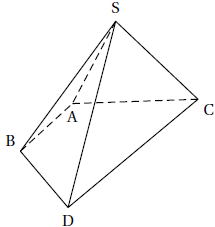
1. Montrer que les points A, B et C ne sont pas alignés.
On montre que les vecteurs AB et AC ne sont pas colinéaires.
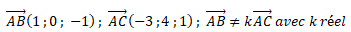
2. a. Montrer que les points A, B, C et D sont coplanaires.
A, B et C n'étant pas alignés, ils définissent un plan. Il suffit de montrer que D appartient au plan (ABC).
On va montrer qu'un vecteur reliant un point de ce plan à D est coplanaire à deux vecteurs non colinéaires du plan(ABC).
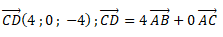
Le vecteur CD étant une combinaison linéaire de 2 vecteurs non colinéaires du plan (ABC), le point D appartient à ce plan.
b. Montrer que le quadrilatère ABDC est un trapèze de bases [AB] et [CD].
On rappelle qu’un trapèze est un quadrilatère ayant deux côtés opposés parallèles appelés bases.
Les vecteurs CD et AB sont colinéaires.
Les segments [AB] et [CD] sont portés par des droites parallèles.
Les points A, B, C et D sont coplanaires.
Le quadrilatère ABCD est plan et possède deux côtés parallèles : c'est donc un trapèze.
3. a. Démontrer que le vecteur n de coordonnées (2 ; 1 ; 2) est un vecteur normal au plan (ABC).
On montre que le vecteur n est orthogonal à deux vecteurs non colinéaires du plan (ABC).
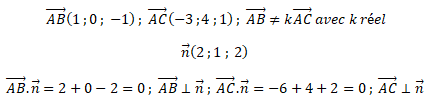
b. En déduire une équation cartésienne du plan (ABC).
2x+y+2z+d=0.
C(0 ; 3 ; 2) appartient à ce plan : 0+3+4+d = 0 ; d = -7.
2x+y+2z -7=0.
c. Déterminer une représentation paramétrique de la droite D passant par le point S et orthogonale au plan (ABC).
Le vecteur n(2 ; 1 ; 2) est un vecteur directeur de cette droite :
x =2t+xS =2t+2 ; y = t+yS = t+1 ; z = 2t+zS =2t+4 avec t réel.
d. On note I le point d’intersection de la droite D et du plan (ABC).
Montrer que le point I a pour coordonnées (2 /3 ; 1 /3 ; 8 /3).
I appartient à cette droite et au plan (ABC) :
2(2+2t) +t+1+2(2t+4)-7 = 0 ; 9t+6 =0 t = -2 /3.
Par suite xI =-4 /3 +2 = 2 /3 ; yI =-2 /3+1 = 1 /3 ; zI =-4 /3+4 =8 /3.
Montrer que SI = 2 cm.
SI2 =(2 /3-2)2 +(1 /3-1)2 +(8 /3-4)2 =16 /9 +4 /9 +16 /9 =36 /9 ; SI = 6 /3 = 2.
4. a. Vérifier que le projeté orthogonal H du point B sur la droite (CD) a pour coordonnées H(3 ; 3 ; −1) et montrer que HB = 3*2½ cm.
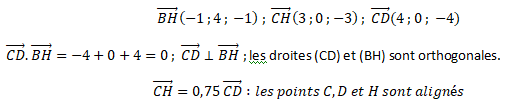
H est le projeté orthogonal de B sur (CD).
BH2 =(-1)2 +42 +(-1)2 = 18 ; BH = 3 *2½.
b. Calculer la valeur exacte de l’aire du trapèze ABDC.
AB2 = 12 +02 +(-1)2 =2 ; AB = 2½.
Or CD = 4 AB ; CD = 4*2½.
Aire du trapèze = demi somme des bases x hauteur = 5*2½ / 2 x 3*2½ = 15 cm2.
5. Déterminer le volume de la pyramide SABDC.
aire de base x hauteur / 3 = 15 x2 /3 = 10 cm3.
|
...
|
....
|
EXERCICE
3 5 points
Dans
la revue Lancet PublicHealth, les chercheurs affirment qu’au 11mai
2020, 5,7% des adultes français avaient déjà été infectés par la COVID
19. Source : https
://www.thelancet.com/journals/lanpub/article/PIIS2468-2667 (21)
00064-5/fulltext
On se servira de cette donnée pour les parties A et B de cet exercice.
Partie A
1. On prélève un individu dans la population française adulte au 11 mai 2020.
On note I l’évènement : « l’adulte a déjà été infecté par la COVID 19 »
Quelle est la probabilité que cet individu prélevé ait déjà été infecté par la COVID 19?
P(I) = 0,057.
2. On prélève un échantillon de 100 personnes de la population supposées choisies de façon indépendante les unes des autres.
On assimile ce prélèvement à un tirage avec remise.
On appelle X la variable aléatoire qui compte le nombre de personnes ayant déjà été infectées.
a. Justifiez que X suit une loi binomiale dont on donnera les paramètres.
On répète N = 100 fois de façon identique une épreuve de Bernoulli dont
le succès " individu choisi déja infecté" a une probabilité p = 0,057.
X compte le nombre de succès.
X suit la loi binomiale de paramètres N =100 et p = 0,057.
b. Calculer son espérance mathématique. Interpréter ce résultat dans le cadre de l’exercice.
E(X) = n p = 100 x0,057 = 5,7.
Dans un échantillon de 100 personnes, 5,7 ont déja été infectés par le virus.
c. Quelle est la probabilité qu’il n’y ait aucune personne infectée dans l’échantillon ?
On donnera une valeur approchée à 10−4 près du résultat.
P(X=0) =(100 0) x0,0570 x0,943100 =0,948100 ~0,0028.
d. Quelle est la probabilité qu’il y ait au moins 2 personnes infectées dans l’échantillon ?
P(X >2 = 1-P(X <1) =1-P(X=0)-P(X=1) =0,9801.
e. Déterminer le plus petit entier n tel que P(X < n)> 0,9.
Interpréter ce résultat dans le contexte de l’exercice.
La calculatrice donne : P(X < 8)=0,8829 et P(X < 9)=0,9408. n = 9.
Sur 100 personnes il y a 9 chances sur 10 que le nombre de personnes
préalablement infectés par ce virus soit inférieur ou égal à 9.
Partie B :
Un test a été mis en place : celui-ci permet de déterminer (même
longtemps après l’infection), si une personne a ou non déjà été
infectée par la COVID 19. Si le test est positif, cela signifie que la
personne a déjà été infectée par la COVID 19.
Deux paramètres permettent de caractériser ce test : sa sensibilité et sa spécificité.
La sensibilité d’un test est la probabilité qu’il soit positif sachant
que la personne a été infectée par la maladie. (II s’agit donc d’un
vrai positif ).
La spécificité d’un test est la probabilité que le test soit négatif
sachant que la personne n’a pas été infectée par la maladie. (II s’agit
donc d’un vrai négatif ).
Le fabricant du test fournit les caractéristiques suivantes :
• Sa sensibilité est de 0,8.
• Sa spécificité est de 0,99.
On prélève un individu soumis au test dans la population française adulte au 11 mai 2020.
On note T l’évènement « le test réalisé est positif ».
1. Compléter l’arbre des probabilités ci-dessous avec les données de l’énoncé :
2. Montrer que p(T ) = 0,05503.
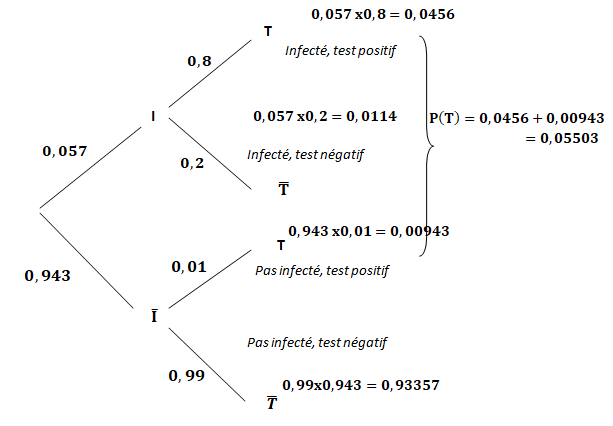
3. Quelle est la probabilité qu’un individu ait été infecté sachant que son test est positif ?
PT(I)=P(I n T) / P(I) =0,0456 / 0,05503 ~0,8286.
Partie C :
On considère un groupe d’une population d’un autre pays soumis au même test de sensibilité 0,8 et de spécificité 0,99.
Dans ce groupe la proportion d’individus ayant un test positif est de 29,44%.
On choisit au hasard un individu de ce groupe; quelle est la probabilité qu’il ait été infecté ?
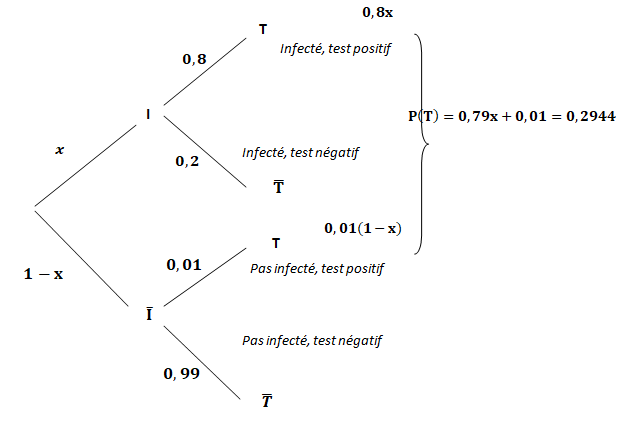
00,79 x = 0,2844 ; x =0,36.
EXERCICE 4 5 points
Pour chacune des affirmations suivantes, préciser si elle est vraie ou fausse puis justifier la réponse donnée.
Toute réponse non argumentée ne sera pas prise en compte.
1. Affirmation 1 : Toute suite décroissante et minorée par 0 converge vers 0. Faux.
Cotre exemple : la suite définie sur N* par un = 1 +1 /n est décroissante et converge vers 1.
2. On considère une suite (un) définie sur N telle que, pour tout entier n,on a
un < (−9n+3n) / 7n .
Affirmation 2 : la limite en +oo de un est -oo. Vrai.
un =-(9 / 7)n [1-1/3)n] .
En plus l'infini : 1/3)n tend vers zéro et -(9 / 7)n tend vers -oo.
3. On considère la fonction suivante écrite en langage Python :
def terme(N) :
U =1
for i in range(N) :
U=U+i
return U
Affirmation 3 : terme(4) renvoie la valeur 7. Vrai.
La boucle for s'exécute 4 fois et le compteur i prend les valeurs 0, 1,2 et 3.
première exécution : U = U+0 = 1
seconde exécution : U+1 devient 2.
troisième exécution : U devient 2+2 =4.
quatrième exécution : U devient 4+3 = 7
4. Lors d’un concours, le gagnant a le choix entre deux prix :
• Prix A : il reçoit 1 000 euros par jour pendant 15 jours;
• Prix B : il reçoit 1 euro le 1er jour, 2 euros le 2e jour, 4 euros le
3e jour et pendant 15 jours la somme reçue double chaque jour.
Affirmation 4 : La valeur du prix A est plus élevée que la valeur du prix B. Faux.
Montant total du prix A : 15 x1000 = 15 000 €.
Montant total du prix B : somme des 15 premiers termes d'une suite géométrique de premier terme 1 et de raison 2 :
(1-215) / (1-2) =215-1 = 32 767.
5. On considère la suite (vn) définie pour tout entier n >1 par
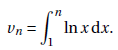
Affirmation 5 : La suite (vn) est croissante. Vrai.
La fonction ln est strictement croissante sur R*+ et ln(1) =0.
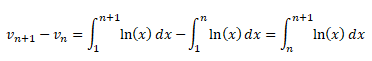
L'intégrale d'une fonction à valeurs positives entre deux bornes ordonnées croissante est positive.
Pour n entier naturel supérieur à1 vn+1-vn est poositive ; la suite (vn) est donc croissante.
|
ane.
|
|
|