Physique
appliquée. Solénoïde.
Concours IESSA 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
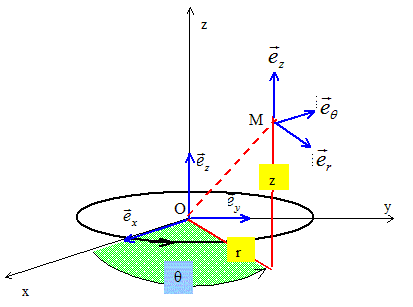
Un solénoïde (S1)
circulaire, d’axe Oz, de longueur h, de rayon a, comporte N1
spires jointives parcourues par un courant d’intensité I1.
On pourra assimiler ce solénoïde à un solénoïde infini car h est très
supérieur à a.
On se place en régime stationnaire.
Question 32 :
Les équations de Maxwell qui régissent la magnétostatique sont :
L'équation
de Maxwell-Faraday et l'équation de Maxwell-Thomson. Réponses
B et D.
La
distance objet - lentille doit être supérieure ou égale à 4 f '. Réponse B.
Question 33.:
Le plan 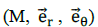 est : est :
A) un plan de symétrie pour les courants. Vrai. B) un plan d’antisymétrie pour
les courants.
Le plan 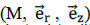 est est
C) u n plan de symétrie pour les courants. D) un plan d’antisymétrie
pour les courants. Vrai.
Tout
plan perpendiculaire à l'axe de la bobine est un plan de symétrie pour
le courant : en conséquence, le champ magnétique est perpendiculaire à
ce plan.
La
distibution de courant étant invariante par rotation autour de l'axe de
la bobine, et par translation sur cet axe, le champ est porté par l'axe
de la bobine et ne dépend que de la distance à l'axe.
Le
champ est nul à l'extérieur de la bobine, car les lignes de champ ne
sortent pas du solénoïde.
Question 34 :
Le champ magnétique est :
A) contenu dans les plans de symétrie pour les courants.
B) orthogonal aux plans de symétrie pour les courants. Vrai.
Les lignes de champ magnétique créées par le solénoïde sont :
C) d es cercles. D) des droites. Vrai.
Question 35 :
En un point M, le solénoïde crée un champ magnétique
B. On admettra qu’à l’extérieur du
solénoïde le champ magnétique est nul.
Dans le solénoïde, le champ magnétique a pour expression :
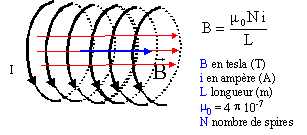 Répondre
E. Répondre
E.
Question 36 :
Le flux propre a pour expression :
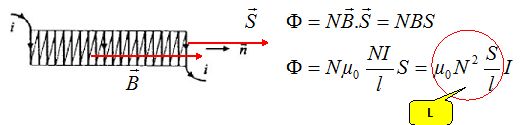
Réponse D.
Question 37.
L’inductance propre L de ce solénoïde a pour expression :
L =µ0 N2 S / h avec S = pa2.
Réponse C.
|
...
|
....
|
Question 38 :
L’énergie magnétique, W , de ce solénoïde a pour expression :
L I2 / 2 = µ0 N2 S I2 / (2h) avec S = pa2. Réponse D.
Question 39 :
Pour les questions 39 et 40, un autre solénoïde (S2) de même axe, de même longueur h et de rayon b (b < a) est inséré dans le solénoïde (S1) précédent. Il comporte N2 spires jointives parcourues par un courant d’intensité I2.
L’inductance mutuelle M de ce système a pour expression :
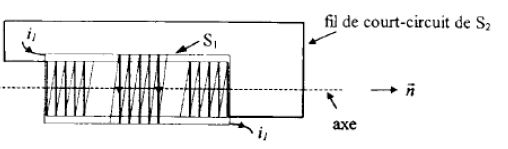
Pour le calcul des flux, la normale n commune aux spires des deux solénoïdes est définie à partir du sens de i1.
Déterminer le flux F1-->2 dû à B1, envoyé par S1 à travers les N2 spires de S2.
B1 = µ0N1 i1/l ; F1-->2 =N2 B1 S2=N2 µ0N1 i1/l S2 = µ0N1N2 i1/l pR22.
En déduire l'expression de la f.é.m induite dans le solénoïde S2 et le sens positif du courant induit i2 pour i1 croissant.
e = -dF1-->2/dt = -µ0N1N2 /l pR22 di1/dt avec di1/dt positif.
e est donc négative et i2 est de sens contraire à i1.
On pose : F1-->2= M21 i1. On appelle mutuelle inductance le coefficient M21.
Déterminer la mutuelle inductance M21 et vérifier qu'elle ne dépend que des nombres de spires et des grandeurs géométriques des circuits.
M21 = µ0N1N2 /l pR22. Répondre E.
Question 40 :
L’énergie magnétique W de ce système a pour expression :
W = ½L1I12 +½L2I22 + M I1 I2.
L1 =µ0 N12 pa2 / h ;
L2 =µ0 N22 pb2 / h. Réponse C.
Question 41 :
Si le solénoïde (S2) garde les mêmes propriétés qu’à la question 39, mais avec un rayon b
supérieur à a, l’inductance mutuelle M’ de ce système a pour expression :
M' = µ0N1N2 / h pa2. Réponse D.
Question 42.
Si le courant I2 dans le solénoïde (S2) est algébrisé dans l’autre sens, l’inductance propre de (S2)
A) change de signe. B) ne change pas de signe, vrai.
L'inductance propre ne dépend pas du sens du courant. L est un coefficient positif.
et l’inductance mutuelle entre (S1) et (S2)
C) change de signe vrai . D) ne change pas de signe.
M est positive ou négative selon l'orientation des circuits.
|
|