Physique
appliquée. Rotation d'une tige, ondes électromagnétiques, lentille.
Concours IESSA 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
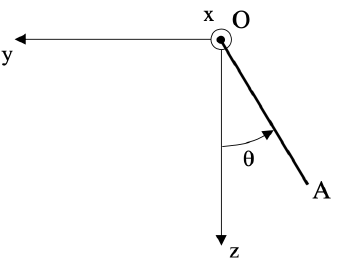
Une tige OA homogène, de masse m
et de longueur L, peut tourner sans frottement autour d’un axe
horizontal (Ox) passant par O.
Son moment d’inertie par rapport à l’axe (Ox) est noté J.
J =m L2 /3.
La tige reste toujours dans le plan (O, y, z).
La base (ex, ey, ez )est orthonormée
directe.
Le référentiel (O, x, y, z) est supposé galiléen.
Le champ de pesanteur est supposé uniforme.
On repère par q
l’angle entre l’axe vertical descendant (Oz) et la tige.
Question 26 :
L’énergie cinétique Ec de la tige a pour expression :
½ J w2
=½ m L2 / 3 w2 =m L2 / 6 (dq/dt)2. Réponse B.
Question 27 :
En choisissant l’origine en z = 0, l’énergie potentielle, Ep,
a pour expression :
Ep =mgz avec z = ½Lcos q ; Ep = ½mg L cos q. Réponse
D.
Question 28 :
Le moment cinétique de la tige par rapport à l’axe (Ox), noté L/Ox
, a pour expression :
OG = ½ L ; v = w
L / 2 ;
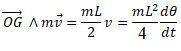 Réponse
B.
Question 29 : Réponse
B.
Question 29 :
Le moment du poids, M, par rapport à l’axe (Ox) a pour
expression :
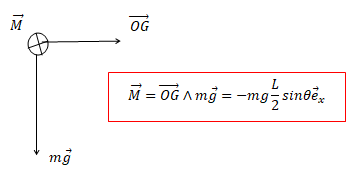
Question
30 :
L’équation différentielle vérifiée par q est :
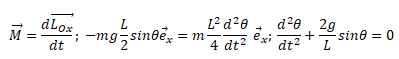 Répondre E. Répondre E.
Question 31.
La période T des petits mouvements autour de l’équilibre a pour
expression :
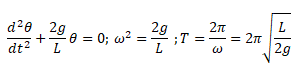 Répondre E. Répondre E.
|
...
|
....
|
Une
onde électromagnétique monochromatique, de pulsation w, se propage dans le vide.
En coordonnées cartésiennes, un point M a pour coordonnées (x, y, z).
Le champ électrique de l’onde électromagnétique en M à l’instant t
s’écrit :
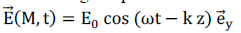 k positif. k positif.
Question 17 :
Indiquer la (ou les) affirmation(s) exacte(s).
A) L’onde se propage suivant ey. B) L’onde se propage
suivant ez.
C) L’onde est plane. Vrai.
D) L’onde n’est pas plane.
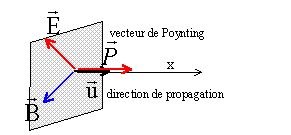
Une onde électromagnétique est la propagation d'un champ électrique E
et d'un champ magnétique B associés, perpendiculaires entre eux et à la
direction de propagation.
Question 18 :
Dans le vide, le champ électromagnétique vérifie les équations :
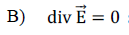
Dans le vide, en absence de charge et de courant, la divergence du
champ électrique est nul.
Question 19 :
A partir des équations de Maxwell, on peut montrer que le champ
électrique vérifie l’équation suivante :
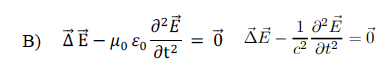
Question 20 :
La célérité c de cette onde électromagnétique s’écrit :
Par suite c2 =1 / ( µ0 e0 ) réponse
D.
Question 21.
En excluant tout champ statique, le champ magnétique a pour expression :
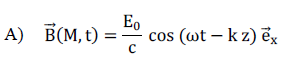
Question 22.
Le vecteur de Poynting s’écrit :
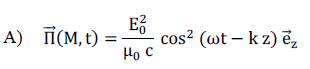
Question 23 :
L’unité du vecteur de Poynting est :
C. watt par m2.
Question 24 :
La densité volumique d’énergie électrique a pour expression :
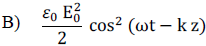
Question 25 :
La densité volumique d’énergie magnétique a pour expression :
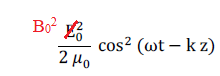
Une lentille mince convergente (L) a pour centre O et
pour distance focale f ’.
Elle est utilisée dans les conditions de Gauss sur un banc d’optique et
donne d’un objet A sur l’axe optique une image A’ sur l’axe optique.
Question 43 :
Un
objet réel AB, perpendiculaire à l’axe optique, ne donne une image
réelle A’B’ sur un écran placé à la distance D de l’objet que si :
La distance objet - lentille
doit être supérieure ou égale à 4 f '.
Réponse B.
Question 44.:
L'une des deux valeurs possibles de p est :
p = [-D+
(D2-4Df ')½] / 2.
Réponse A.
Question 45 :
L'autre valeur est :
p = [-D- (D2-4Df ')½] / 2.
Réponse A.
Question 46 :
La distance d entre ces deux positions a pour
expression :
d2 =D2-4Df'. Réponse
B.
Question
47 :
Pour D = 1 m, on mesure d = 20 cm. La lentille a donc pour distance
focale image :
4Df ' =D2-d2 =1-0,22 =0,96 ; f '
= 0,96 / 4 = 0,24 m = 24 cm. Réponse
D.
|
|