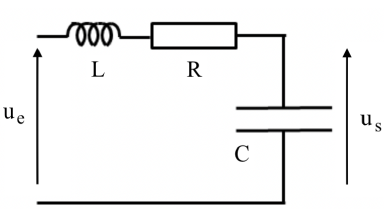
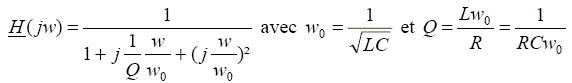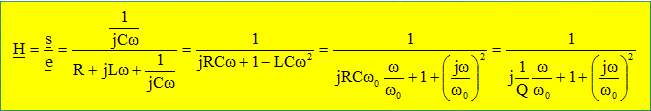Physique appliquée. Filtre passe bas du second ordre. Concours IESSA  2023.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
On étudie le filtre linéaire ci-dessous.

Question 1 :
A basse fréquence, un condensateur se comporte comme
A) un interrupteur ouvert. Vrai .B) un fil.
Z = 1 / (Cw) ; si w est très faible, à C constant, Z est grand.
A haute fréquence, un condensateur se comporte comme
C) un interrupteur ouvert. D) un fil. Vrai.

Question 2 :
A basse fréquence, une bobine idéale se comporte comme
A) un interrupteur ouvert. B) un fil. Vrai.
Z= L w ; si w est très faible, à L constant, Z est faible.
A haute fréquence, une bobine idéale se comporte comme
C) un interrupteur ouvert. Vrai. D) un fil.

Question 3 :
Le filtre est un
A) passe - bas. Vrai.  B) passe-haut.
C) passe-bande.   D) coupe-bande.

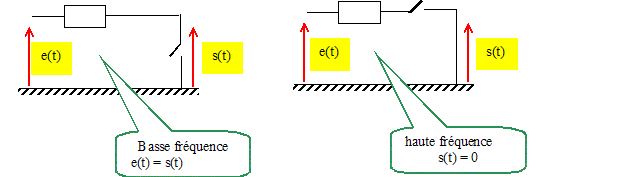
Le filtre coupe les hautes fréquences, mais laisse passer les basses fréquences : filtre passe bas.

Question 4 :
La fonction de transfert a pour forme canonique :

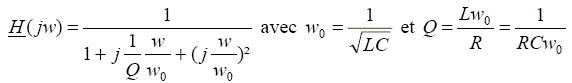
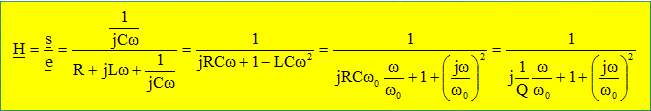
Question 5 :
Dans la forme canonique de ce filtre, H0 a pour expression : H0 = 1. Réponse B.

Question 6.
L’expression de w0 est : w0 =1/(LC)½. Réponse B.

Question 7 :
Le facteur de qualité Q a pour expression :Q = L½ / (R C½). Réponse D.

Question 8 :
A basse pulsation, le diagramme de Bode en gain a pour pente :
On appelle gain, la fonction , telle que GdB= 20 log H .
On pose x = w2/w20  ;GdB= -10 log [(1-x2)2+Q-2x2 ]

si x tend vers 0, alors GdB est équivalent à 0. L'axe des abscisses est asymptote horizontale. Réponse A.

si x tend vers l'infini, alors GdB est équivalent à -40 log x. ( droite de pente -40 dB par décade).

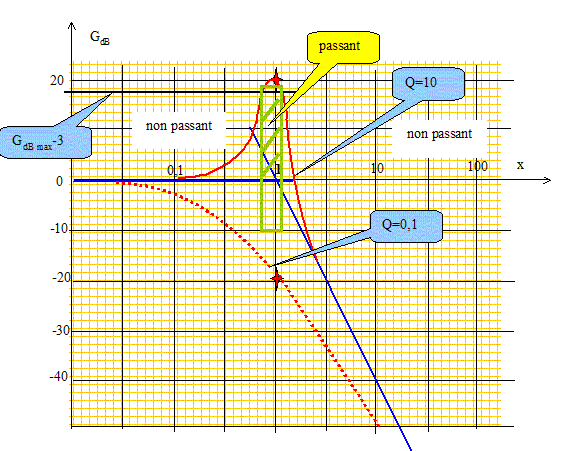
 Question 9 :
A basse pulsation, le filtre a un comportement :
A) intégrateur. B) dérivateur.
C) double intégrateur. D) double dérivateur.
Un filtre passe-bas du deuxième ordre est ni dérivateur, ni intégrateur. Les asymptotes dans le diagramme de Bode ont des pentes 0 dB/ décade ou ±40 dB/décade.

Question 10 :
A basse pulsation, le déphasage de us par rapport à ue tend vers :
p/2 ; -p/2 ; 0. ; p.

diagramme de Bode de la phase :

j = -tan-1 ( x / [Q(1-x²)] )si 1-x² >0

recherche des asymptotes :

lorsque x tend vers 0+, j tend vers 0-: l'axe des abscisses est asymptote.

j = p + tan-1 ( x / [Q(1-x²)] ) si 1-x² < 0

lorsque x tend vers l'infini, j tend vers -p+ : la droite j = -p est asymptote.

valeur particulière j(1) = -½ p .

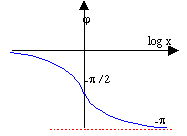
Question 11 :
A haute pulsation, le diagramme de Bode en gain a pour pente :
D) − 40 dB/déc.

Question 12 :
A haute pulsation, le filtre a un comportement :
A) intégrateur. B) dérivateur.
C) double intégrateur. D) double dérivateur.

...
....

 Question 13 :
A haute pulsation, le déphasage de us par rapport à ue tend vers :
p/2 ; -p/2 ; 0. ; p.

Si x tend vers l'infini, f tend vers  -p.



Question 14 :
A la pulsation w0 , le déphasage de us par rapport à ue vaut :
p/2 ; -p/2 ; 0. ; p.


Question 15 :
A la pulsation w0 , le gain du filtre vaut :
G = R(C /L)½ ; G=0 ; G=1 ; G = 1/R (L/C)½.
On pose x = w2/w20  ;GdB= -10 log [(1-x2)2+Q-2x2 ].
x = 1  ; Q = L½ / (R C½) ; 1/Q2 =R2C / L.
GdB = 10 log (R2C / L).

Question 16 :
L’équation différentielle reliant ue et us est :

e = 1/(Qw0) jw +1/w02 (jw)2+1]s.

à jw correspond ds/dt ; à (jw)2 correspond d2s/dt2.

d'où : e(t) =1/w02d2s/dt2 +1/(Qw0) ds/dt + s(t)

w02 = 1 / LC ; Qw0 = 1 / (RC).
e(t) =LC d2s /dt2 +RC ds /dt +s(t). Réponse C.

  
menu