Mathématiques.
Concours IESSA 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
|
...
|
....
|
Soient f et g les fonctions
définies sur ]0 : +oo[ par :
f(x) = ln(x) et g(x) = 2 x½ / e.
h(x) = g(x) -f(x).
Question 11.
La dérivée de h(x) est :
h '(x) = g '(x) -f '(x) = x-½ / e - 1 / x =(x-ex½
)/ (e x1,5). Réponse D.
Question 12. On en
déduit que :
(e x1,5) > 0 ; x½ > 0 ; x-ex½
= x½(x½-e).
Le signe de h '(x) est celui de x½-e :
si x > e2, h'(x) >0 et h est strictement croissante.
si x < e2, h'(x) < 0 et h est strictement
décroissante. Réponse B.
Question 13.
L’étude des valeurs atteintes par la fonction nous permet d’affirmer
que :
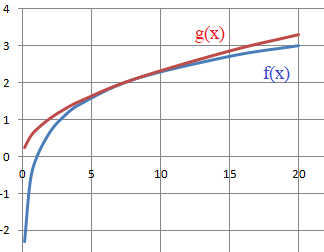
f(x) < g(x) sur ]0
; +oo[ . Réponse D.
Question 14.
Des fonctions F(x) et G(x) primitives de f(x) et g(x) sont :
F(x) = x ln(x) -x ; G(x) = 4x1,5 / (3e). Réponse B.
Question 15
Ainsi, la valeur de I est :
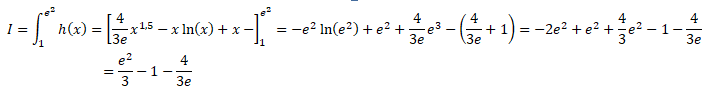
Réponse C.
Question 16
La matrice définie par :
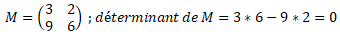
Le déterminant étant nul, M n'est pas inversible. Réponse A.
Question 17
On en déduit que le système linéaire :
3x+2y = 5 et 9x+6y=15.
admet une infinité de solutions. Réponse D.
Question 18
Soit le système linéaire : 3x-2y = 5 et -5x+3y = -9.
Le système peut s’écrire sous la forme :
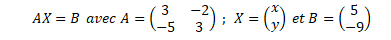
Réponse B.
Question 19
Ainsi, on en déduit que :
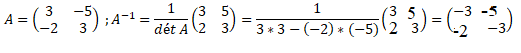
Réponse B.
Question 20
La solution du système est alors :
3x-2y = 5 et -5x+3y = -9.
9x-6y = 15 et -10x+6y = -18.
-x =-3 ; x = 3 et y = 2.
Réponse C.
|
|