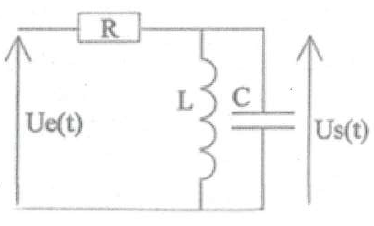
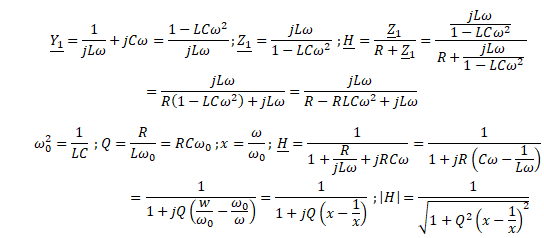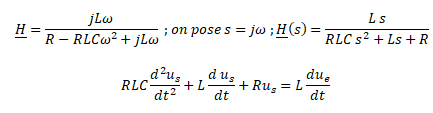Physique appliquée, concours ingénieur IESSA  2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Partie 1. Une barre cylindrique de rayon a, d'axe Ox a de longueur L. Sa conductivité thermique est notée K, sa masse volumique µ et sa capacité massique c. Elle est parfaitement calorifugée sur sa face latérale. La température ne dépend que de la variable spatiale x et du temps t. Q1. La conduction thermique dans la barre est réglée par la loi de Fourier. 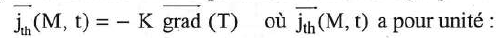W m-2. J s-1 m-2. Réponses A et D. 2. La loi de Fourier est analogue à la loi d'Ohm locale en électricité. En conduction électrique, la grandeur analogue à la température est le potentiel électrique.  Réponse B. En conduction électrique, la grandeur analogue à la puissance thermique est la puissance électrique. Répondre E. 3. L'unité de K est W m-1 K-1. Réponse D. 4. L'équation locale ( équation de diffusion ) vérifiée par la température s'écrit : 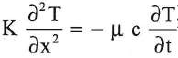. Réponse C. 5. A L'ordre de  grandeur d'un temps caractéristique t d'évolution de la température est : t s'exprime en seconde ; K s'exprime en W m-1 K-1= J s-1 m-1 K-1. µ s'exprime en kg m-3 ; c s'exprime en J kg-1 K-1. µcL2 / K est homogène à un temps. Réponse D. 6. Une barre de même rayon, de longueur L', de conductivité thermique K', de masse volumique µ' et pour capacité thermique massique c', parfaitement calorifugée sur sa surface latérale, est juxtaposée à la précédente en x = L. En x=0 on maintient la température fixe à T1 et en x=L+L' à T2. En régime stationnaire, la puissance thermique traversant l'ensemble est : Le flux est identique dans les deux barres : association de résistances thermiques notées Rth et R'th en série. Rth = L /(Kpa2) ; R'th = L' /(K'pa2) ; Rth + R'th=(LK'+L'K) / (KK'pa2). Flux thermique = (T1-T2) / (Rth + R'th) =KK'pa2(T1-T2) / (LK'+L'K). Réponse C. 7. La température de contact Tc entre les deux barres en x=L s'écrit : Le flux de chaleur est constant en régime stationnaire. Les sections des barres sont identiques.La densité du flux de chaleur est la même dans les barres. La loi de Fourier conduit à : K(Tc-T1) / L =K'(T2-Tc) / L'. KL'Tc -KL'T1 = K'LT2 -K'LTc. Tc(KL'+K'L) = KL'T1 +K'LT2. Tc=(KL'T1 +K'LT2) / (KL'+K'L). Réponse A. 8. La température dans la première barre s'écrit : Le flux de chaleur est constant en régime stationnaire. Il en est de même du gradient de température  dT /dx = (Tc-T1) / L T = (Tc-T1) / L x + Cste. T(x=0) = T1 ; Cste = T1. T = (Tc-T1) / L x +T1. Réponse A. et dans la deuxième barre : T = (T2-Tc) / L' x + Cste. T(x=L+L') = T2 ; Cste =T2 - (T2-Tc) (L+L') / L'. T = (T2-Tc) / L' x +T2-(T2-Tc) (L+L') / L'. T = Tc+(T2-Tc) / L' (x-L). Réponse C. 9. Si K << K' et si L et L' sont du même ordre de grandeur, l'expression approchée de Tc est :). Tc=(KL'T1 +K'LT2) / (KL'+K'L). Tc ~ (KL'T1 +K'LT2) / (K'L) ~(KT1 +K'T2) / K' ~T2. Réponse B. 10. Avec les mêmes hypothèses, l'expression approchée de Pth est : Pth =KK'pa2(T1-T2) / (LK'+L'K)~KK'pa2(T1-T2) / (LK')~Kpa2(T1-T2) / L. . Réponse C. Partie II. Un point matériel M de masse m glisse sans frottement sur une tige Ox horizontale tournant à la vitesse angulaire constante w autour de Oz0. Le point M est relié à un ressort de raideur k, de longueur à vide L0 dont l'autre extrémité est le point O. w diffère de (k/m)½. 11. 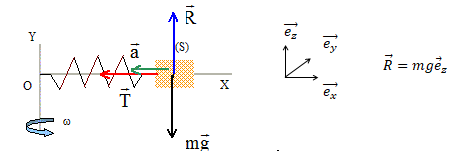Lorsque le point M est à l'équilibre par rapport à la tige, la longueur du ressort xéq s'écrit : La masse S est soumise à son poids, à l'action du support perpendiculaire au support ( et opposée au poids) et à la tension proportionnelle à l'allongement du ressort.Suivant l'axe n de la base de Frenet , la somme vectorielle des forces s'écrit :  T= k(xéq-L0) = mw2 xéq. xéq(k-mw2)=kL0 ; xéq = kL0 / (k-mw2). Répondre E. 12. La réaction de la tige sur le point M a pour expression R = mg.  réponse D. 13. Lorsque M est en mouvement, l'équation différentielle vérifiée par x s'écrit : Le référentiel n'est pas galiléen, il faut prendre en compte la force d'inertie  d'entraînement : -k(x-L0) +mw2x= md2x/dt2. md2x/dt2+(k-mw2)x = kL0. . Réponses B. Dans les questions suivantes, à l'instant initial t=0, M est immobile par rapport à la tige et le ressort a pour longueur L0. 14. Pour w < (k/m)½, on pose W1 =(k/m-w2)½. Equation homogène : d2x/dt2+W1 2x =0. Equation caractéristique r2 +W1 2 =0 ; le discriminant -4W1 2 est négatif. x(t) a pour expression : x= A cos (W1t) + Bsin (W1t) +kL0 / (k-mw2). x= A cos (W1t) + Bsin (W1t) +xéq. Les conditions initiales permettent de trouver A et B. x(t=0)= A+xéq = L0 ; A = L0 -xéq. x' =-AW1 sin (W1t) +BW1 cos (W1t). x'(t=0) =BW1  = 0 ; B = 0. x = (L0 -xéq)cos (W1t)+xéq.  réponse A. Q15. Dans ce cas, la réaction de la tige sur le point M a pour expression :. Réponse B. Q16. Le portrait de phase a l'allure suivante :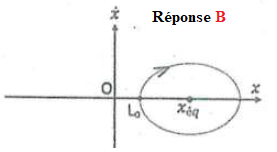 17. Pour w > (k/m)½, on pose W2 =(w2-k/m)½. x(t) a pour expression : Equation homogène : d2x/dt2+W2 2x =0. Equation caractéristique r2 +W2 2 =0 ; le discriminant 4W2 2 est positif. x = A exp(W2t) +Bexp(-W2t) +xéq. Les conditions initiales donnent : x (t=0)= A +B +xéq = L0. x'(t) = AW2exp(W2t) -BW2exp(-W2t). x'(t=0) =AW2-BW2 =0 ; A =  B. 2A  +xéq = L0 ; A = (L0-xéq) /2. x =  (L0-xéq) /2 [exp(W2t) +)exp(-W2t)] +xéq. x =(L0-xéq)cosh(W2t) +xéq. Réponse C. La masse est animée d'un mouvement rectilgne qui conduit à la rupture du ressort. 18. Dans ce cas la réaction de la tige a pour expression : R = mg. Répondre E. 19. Le portrait de phase a l'allure suivante :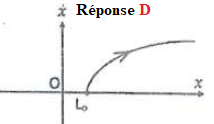 ... .... 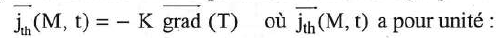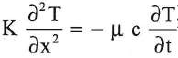Partie III. On étudie le filtre linéaire suivant : 20. A basse fréquence, un condensateur se comporte comme un interrupteur ouvert. Réponse B. Z = 1 / (jCw) ; si w tend vers zéro, Z tend vers l'infini. A haute fréquence, un condensateur se comporte comme un fil. Réponse C. Z = 1 / (jCw) ; si w tend vers l'infini, Z tend vers zéro. 21. A basse fréquence, une bobine idéale se comporte comme un fil. Réponse A. Z = jLw ; si w tend vers zéro, Z tend vers zéro. A haute fréquence, une bobine idéale se comporte comme un interrupteur ouvert. Réponse D. Z = jLw ; si w tend vers l'infini, Z tend vers l'infini. 22. Le filtre est un passe-bande. Réponse B. 23. La fonction de transfert a pour expression :    Réponse D. Le gain est maximum si x = 1 soit w = w0. 24. A basse pulsation, le diagramme de Bode a pour pente : x << 1 : H ~ j x / Q. Gain G =x / Q ; GdB = -20 log (Q) + 20 log(x) ; droite de pente + 20 dB. Réponse B 25. A basse pulsation, le filtre a un comportement dérivateur. Réponse B. Le gain est proportionnel à la fréquence. 26. A basse pulsation, le déphasage de us par rapport à ue tend vers : f = arg(j x / Q) = p /2. Réponse A. 27. A haute pulsation, le diagramme de Bode a pour pente : x >> 1 ; H ~ 1 /(jQx) ; G ~1 /(Qx) ; GdB =-20 log(Q) - 20 log(x). Droite de pende -20 dB. Réponse C. 28. A haute pulsation, le filtre a un comportement intégrateur. Réponse A. 29. A haute pulsation, le déphasage de us par rapport à ue tend vers : x >>1 ; f = arg(1/ (jQx)) = -p /2. Réponse B. 30. A la pulsation w = (1 / (LC))½, le déphasage de us par rapport à ue vaut : f = arg(1) = 0. Réponse C. 31. A la pulsation w = (1 / (LC))½, le gain du filtre vaut G = 1. Réponse C. 32. L'équation différentielle reliant ue et us est : Réponse D. Partie IV. On considère deux sphères concentriques de centre O, de rayons R1 et R2 ( R2 > R1) chargées uniformément en surface avec une charge surfacique s1 et s2 respectivement séparées par du vide de permitivité électrique e0. On se place en régime stationnaire. Un point M de l'espace est repéré par les coordonnées sphériques. 33. Le champ électrique est radial. Contenu dans les plans de symétrie pour les charges. Les lignes de champs sont des droites. Réponses A et D. 34. Le système étant globalement neutre, s1 et s2 sont reliés par la relation : 4pR12 s1 + 4pR22 s2 = 0 ; R12 s1 + R22 s2 = 0  . Réponse D. 35. Pour r < R1 le champ électrique en M s'écrit E(M) = 0. Réponse B. On considère les contributions individuelles de chaque sphère et on les additionne. Appliquer le théorème de Gauss en considérant une surface sphérique de centre O et de rayon r < R1. 36. Pour R1 < r < R2 le champ électrique en M s'écrit : Appliquer le théorème de Gauss en considérant une surface sphérique de centre O et de rayon r : Pour la sphère de rayon R1 : E1 = Q1/ (8 p e0 r2) avec Q1 =4pR12 s1. E1 =R12 s1 /(2e0 r2). Pour la sphère de rayon R2 : E2 = 0. E1 +E2=R12 s1 /(2e0 r2). Répondre E. 37. Pour r > R2 le champ électrique en M s'écrit : Pour la sphère de rayon R1 : E1 = Q1/ (8 p e0 r2) avec Q1 =4pR12 s1. E1 =R12 s1 /(2e0 r2). Pour la sphère de rayon R2 : E2 = Q2/ (8 p e0 r2) avec Q2 =4pR22 s2. E2 =R22 s2 /(2e0 r2). E1 +E2=1/(2e0 r2) [ R12 s1 + R22 s2] =0.  Réponse B. 38. Le potentiel électrique en M est noté V(M). L'origine des potentiel est en r = 0. Pour r < R1, il s'écrit : E = -dV / dr ; dV = -E dr. E1=0 ; intégrer : V(M) =  cste = 0. Réponse B. 39. Pour R1 < r < R2 , il s'écrit : E =R12 s1 /(2e0 r2) ; dV = -E dr. Intégrer entre R1 et r : V =  R12 s1 /(2e0 ) ( 1 / r - 1/R1). Répondre E. 40. Pour r > R2, il s'écrit : E=0 ; dV = -E dr ; intégrer : V(M) =  cste = V(R2)= R12 s1 /(2e0 ) ( 1 / R2 - 1/R1)..  Répondre E. 41. La charge Q de la sphère intérieure est s1 4 pR12. Réponse A. 42. La capacité de ce condensateur sphérique est définie par Q = C(V(R1) -V(R2)). Son expression est : V(R1) -V(R2)=Q / (4 p e0) [1/R1-1/R2]= Q / (4 p e0) [R2-R1] / (R2R1). C = 4 p e0 R2R1 / [R2-R1]. Réponse A.

menu