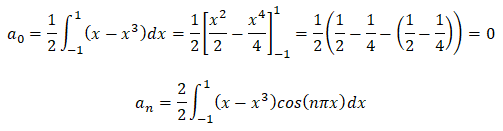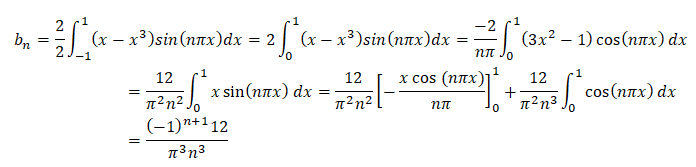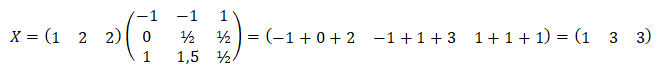Partie 1.
Soit la fonction f périodique de période 2 vérifiant f(x) = x-x
3 pour x appartenant à ]-1 ; 1].
Q1. Dans le développement en série de Fourier de f :
La fonction est impaire, a0=0, an = 0 avec n > 0.
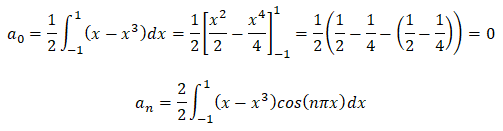
Réponse C.
Q2. Le développement en série de f s'écrit :
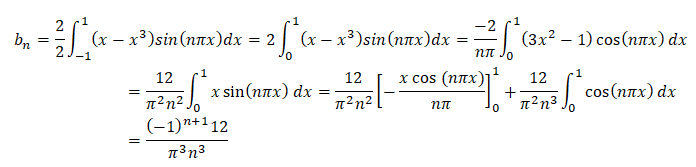
Première intégration par parties : u' = sin(n
px) ; v=x-x
3 ; u = -cos(
npx) / (n
p) ; v'= 1-3x
2.
Seconde intégration par parties :
u' = cos(npx) ; v=1-3x2 ; u = sin(npx) / (np) ; v'= -6x.
Réponse B.
Q3. Soit la fonction f définie sur R/{2} par f(x) =y = (x+3) / (x-2).
La fonction f est inversible et sa fonction réciproque g est définie sur /{a} par :
On intervertit x et y : x = (y+3) / (y-2).
On isole y : y+3 =xy-2x ; y-xy =-2x-3 ; y = (-2x-3) /(1-x)= (2x+3) / (x-1) avec x différent de 1.
Réponse A.
Partie II.
Soit la fonction h définie sur R par h(x) = (ex-e-x) / (ex+e-x).
Q4.
La fonction h admet une application réciproque h
-1 définie sur J à valeurs dans I, avec :
x =(ey-e-y) / (ey+e-y).
x(ey+e-y) =ey-e-y ; ey(x-1) =e-y(-x-1) ; y+ln(x-1)=-y +ln(-x-1).
2y =ln(-x-1) -ln(x-1) =ln[(-x-1) / (x-1)]
y =h-1(x)= 0,5 ln[(x+1) / (1-x)].
(x+1) / (1-x) >0 soit x appartenant à J =]-1 ; 1[ et I = ]-oo ; +oo[.
Répondre E.
Q5. La fonction h vérifie :
On pose u = e
x-e
-x et v =
ex+e-x ; u' = ex+e-x et v' = ex-e-x ;
h'(x)=(u'v-v'u) / v2 = (ex+e-x )2-(ex-e-x )2] / (ex+e-x )2= 4 / (ex+e-x )2.
1-h(x)2 =1-(ex-e-x)2 / (ex+e-x)2=[(ex+e-x)2-(ex-e-x)2 ] /(ex+e-x)2=4 / (ex+e-x )2.
1-h(x)2 =h'(x).
Réponse
C.
Q6. On en déduit que la fonction h
-1 est dérivable sur J et :
[h
-1] '(x) = 1/ [ h ' h
-1(x)]......
Q7. On montre que 1 /(x
2-1) =A /(x+1) +B/(x-1) =[Ax-A +Bx+B) /
(x2-1).
On identifie A+B=0 soit A = -B et B-A = 1 soit B = 0,5.
1 /(x2-1) = -0,5 /(x+1) +0,5/(x-1). Réponse D.
Q8.
On en déduit que : h-1(x) = 0,5 ln[(x+1) /(1-x)].
Réponse C.
Q9. Dans le cas d'un régime
pseudopériodique z'(t) = A exp(-t / t')cos ( W't+f). t' a pour expression :
r2 +9 / 2 h / (ra
a2)
r +3k/(4praa3)
=0.
1/ t'=9 / 4 h
/ (ra a2) ; t' = 4 ra a2 / (9h).
. Réponse D.