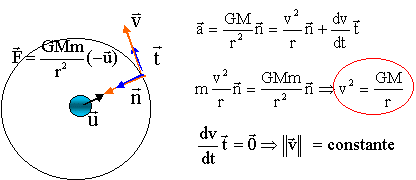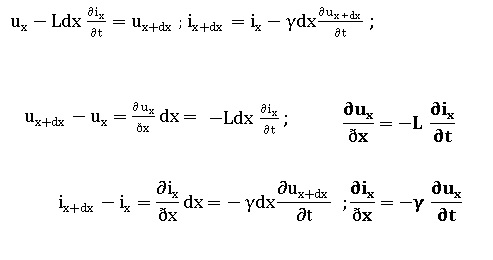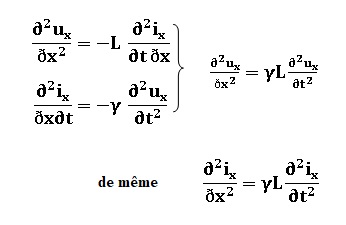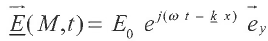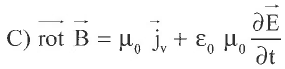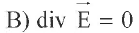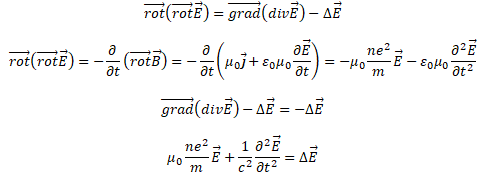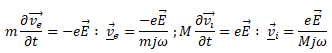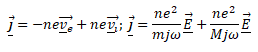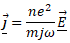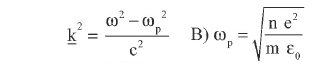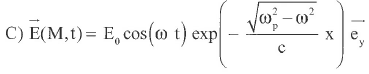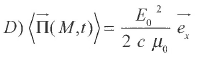Physique
appliquée.
Concours IESSA 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Partie
1.
La terre a pour centre O, pour rayon RT et pour masse MT. Sa distribution de masse est a symétrie sphérique.
Question 1.
Le référentiel géocentrique est noté Rg.
Rg a pour centre O et ses axes pointent vers trois étoiles fixes.
Il est supposé galiléen car la durée d'étude est très inférieure à un an.
Réponses A et D.
Question 2.
Un
satellite assimilé à un point matériel M de masse m n'est soumis qu'à
l'attraction gravitationnelle de la terre.L 'unité de la constante de
gravitation universelle G est : N m2 kg-2.
Réponse C.
Question 3. L'ordre de grandeur de G est 6,67 10-11. Réponse A.
Question 4. Au cours de ce mouvement :
l'énergie mécanique se conserve.
le moment cinétique se conserve.
Réponses A et C.
Question
5.
Le mouvement du point M est plan car :
le mouvement est à force centrale. Réponse A.
Question 6.
En coordonnées polaires, l'énergie cinétique a pour expression :
Coordonnées du vecteur vitesse : r' ; rq'.
Energie cinétique : ½m ( r'2 + (rq')2).
Réponse C.
Question 7.
La constante des aires a pour expression : C = r2 q'. Réponse D.
Question
8.
On définit l'énergie potentielle effective par : Epeff (r)=½ m C2 / r2 -G MT m / r.
Réponse D.
Question 9.
EM = ½m r'2 +Epeff (r).
On a toujours EM >Epeff (r). Réponse D.
Question 10.
Un état lié correspond à EM < 0.
Réponse A.
Question 11.
La vitesse de libération ou deuxième vitesse cosmique a pour expression vL=(2GMT / RT)½.
Réponse C.
Question 12.
vL ~ (2 x 6,7 10-11 x 6 1024 / (6,4 106))½~(1,3 108)½ ~1,1 104 m /s ~11 km /s. Réponse C.
Question 13.
Pour la suite le satellite a un mouvement circulaire uniforme de rayon constant r. L'expression de la vitesse est :
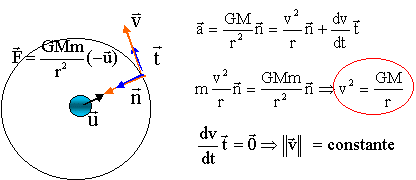
Réponse B.
Question 14.
L'énergie mécanique a pour expression :
Energie cinétique : Ec = ½mv2, remplacer v2 par GM / r.
Ec = ½m GM / r.
Energie mécanique : Em = Ep + Ec = -m GM / r + ½m GM / r = -½m GM / r . Réponse C.
Question 15.
La période du satellite a pour expression :
La période est la durée pour pacourir une circonférence de rayon r à la vitesse v.
2pr = vT.
4p2r2 = v2T2 = GMT2 / r.
T2 = r3 4p2/ (GM). Réponse A.
Question 16.
La vitesse en orbite basse, ou première vitesse cosmique, a pour expression :
vo.b =(GM / R) ½. Réponse B.
Question 17.
Sa valeur vaut :(6,7 10-11 x 6 1024 / (6,4 106))½~8 103 m/s. Réponse B.
|
...
|
....
|
Partie II câble coaxial.
Une portion de câble coaxial comprise entre x et x+dx a pour modèle :
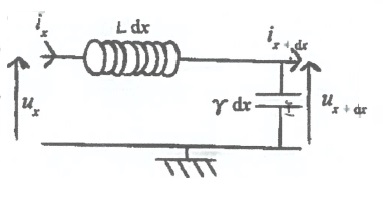
dL = Ldx avec L inductance linéique. dC = g dx capacité linéique.
Questions 18 et 19.
A partir d'une loi des noeuds on obtient :
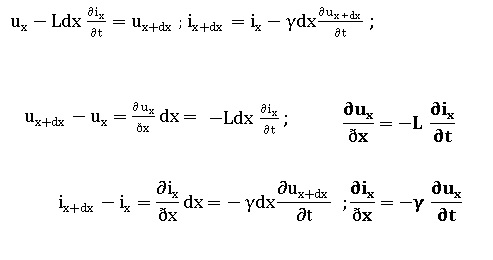
Réponse B.
Question 20.
L'équation de propagation vérifiée par le courant s'écrit :
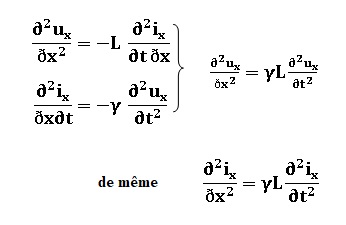
Réponse C.
Question 21.
La célérité V de l'onde de courant a pour expression :.
v = 1 /(gL)½
= 1/ (e0
er
µ0)½ . Réponse C.
Question 22.
Une onde plane progressive harmonique de pulsation w se propage dans le câble.
Le courant s'écrit sous la forme i(x,t) =I1 cos (wt-kx) avec k > 0.
L'expression de la relation de dispersion est : w = k V réponse A.
Cette onde se propage suivant les x croisants.
Question 23
L'onde de tension a pour expression :
dux/dx = -L dix/dt.
dix/dt = -I1 w sin (wt-kx).
dux/dx = L I1 w sin (wt-kx).
ux = L w / k I1 cos (wt-kx).
ux = L v I1 cos (wt-kx).
ux = (L / g)½ I1 cos (wt-kx).
Réponse B.
Question 24
Une onde plane progressive harmonique de pulsation w se propage dans le câble.
Le courant s'écrit sous la forme i(x,t) =I2 cos (wt+kx) avec k > 0.
L'onde de tension a pour expression :
dux/dx = -L dix/dt.
dix/dt = -I2 w sin (wt+kx).
dux/dx = L I2 w sin (wt+kx).
ux = -L w / k I2 cos (wt+kx).
ux = -L v I2 cos (wt+kx).
ux = -(L / g)½ I2 cos (wt+kx).
Réponse A.
Question 25
Une onde plane progressive harmonique de pulsation w se propage dans le câble.
Le courant s'écrit sous la forme i(x,t) =I1 cos (wt-kx) +I2 cos (wt+kx) avec k > 0.
L'onde de tension a pour expression :
ux = (L / g)½ I1 cos (wt-kx)-(L / g)½ I2 cos (wt+kx)..
. Réponse A.
Partie IV.
Un
plasma est un milieu localement neutre constitué d'ions positifs de
masse M, de charge +e et de concentration n ( nombre d'ions par m3) et d'électrons de masse m, de charge -e et de concentration n. On négligera les interactions entre ces charges.
On étudie une onde harmonique de pulsation w dans ce plasma.
En un point M(x, y,z) le champ électrique de cette onde s'écrit en notation complexe
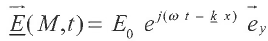
Question 37
L'équation de Maxwell-Ampère dans le plasma s'écrit :
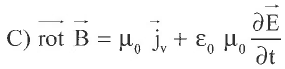
Question 38.
L'équation de Maxwell-Gauss dans le plasma s'écrit sous la forme :
Le milieu étant localement neutre : 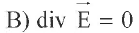
Question 39.
A partir des équations de Maxwell, on peut montrer que le champ électrique vérifie :
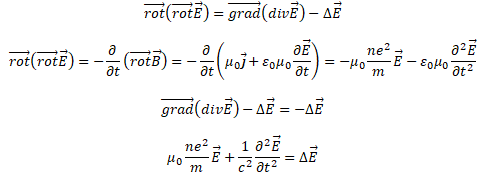
Réponse D.
Question 40.
En négligeant la force magnétique devant la force électrique, les vitesses vi d'un ion et ve d'un électron ont pour expression en notation complexe :
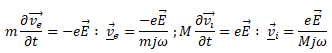
Réponses A et D.
Question 41.
Le vecteur densité volumique de courant a pour expression en notation complexe :
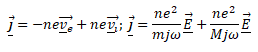
Réponse D.
Question 42.
Pour toute la suite de cette partie, on se place dans le cas où M >> m. L'expression ci-dessus devient alors.
En négligeant le déplacement des cations beaucoup plus lourds que les électrons :
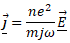
Question 43.
Le courant dans le plasma est principalement dû aux électrons ( réponse A).
Le vecteur densité volumique de courant et le champ électrique sont en quadrature de phase ( réponse C).
Question 44.
k et w sont liés par la relation de dispersion avec wp la pulsation plasma.
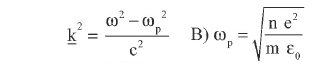
Question 45.
Dans toutes les questions suivantes, le plasma s'étend dans le demi-espace x > 0.
Pour w < wp, le champ électrique a pour expression réelle :
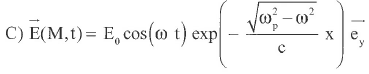
Question 46.
Pour w < wp, le champ électrique est une onde stationnaire décroissante ( onde évanescente, onde qui s'attéhue sans se propager). Réponse D.
Question 47.
Pour w < wp, le champ électrique est une onde plane Réponse A.
Question 48.
Pour w < wp, la valeur moyenne dans le temps du vecteur de Poynting est nulle ( réponse A)
Il n'y a pas d'énergie transférée au plasma ; le plasma se comporte comme un miroir pour les ondes de pulsation inférieure à wp.
Question 49.
Pour w > wp, le champ électrique a pour expression réelle :

Question 50.
Pour w > wp, la valeur moyenne dans le temps du vecteur de Poynting est :
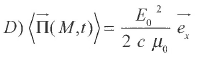
|
|