Mathématiques.
Concours IESSA 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
|
...
|
....
|
Partie III.
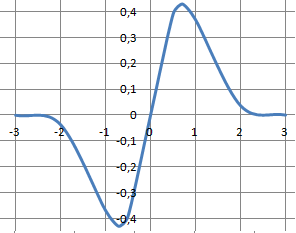
Soit la fonction f définie sur R par f(t) = t exp(-t2).
Question 11.
La fonction f est impaire car f(-t) = -t exp(-t2)= - f(t). Réponse D.
Question 12. Le calcul de la dérivée de f donne :
on pose u = t et v = exp(-t2) ; u' = 1 ; v' = -2t exp(-t2) ;
u'v+v'u =exp(-t2) -2t2 exp(-t2) = (1-2t2) exp(-t2) .
Réponse D.
Question 13.
On peut en déduire que la fonction f est :
exp(-t2) >0 ; f '(t) a le signe de 1-2t2.
Si t appartient à [-2½ /2 ; 2½ /2], f '(t) >0 et f(t) est croissante. Réponse A.
Si t appartient à ]-oo ; -2½ /2 ] union [ -2½ /2 ; +oo[ , f '(t) < 0 et f(t) est décroissante. Réponse D.
Question 14.
Les limites de f aux bornes de l'ensemble de définition sont :
Limite en -oo : exp(-t2) tend vers zéro et f(t) tend vers zéro.
Limite en +oo : exp(-t2) tend vers zéro et f(t) tend vers zéro.
Réponse B.
Question 15
Le calcul suivant donne :
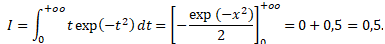
Réponse D.
Question 16
La fonction f est développable en série entière et on a : f(t) =t-t3+x5/2-x7/6+x9/24+ ... +(-1)n t2n+1 / n!.
Réponse B.
Partie IV.
On considère la matrice A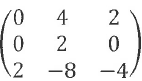
Question 17
Déterminant de A : 0*2*-4 +4*0*2+2*-8*0- 2*2*2 -0*4*(-4)-0*0*(-8) = -8.
dét(A) diffère de zéro, A est inversible.. Réponse B.
Question 18
La matrice A2 vaut :
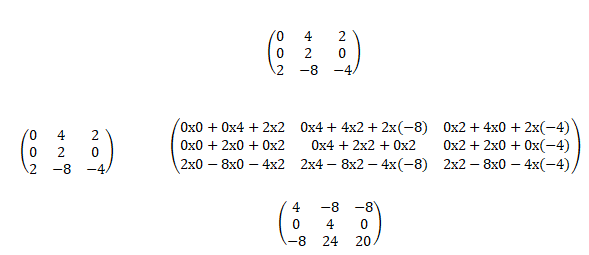
Réponse B.
Question 19
En calculant A3+2A2-12A on obtient :
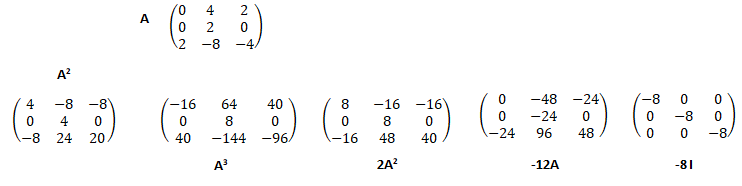
Réponse D.
Question 20
L'inverse de A est alors :
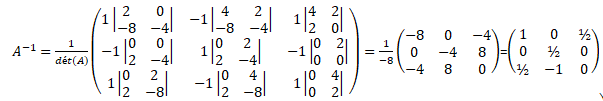
Réponse D.
|
|