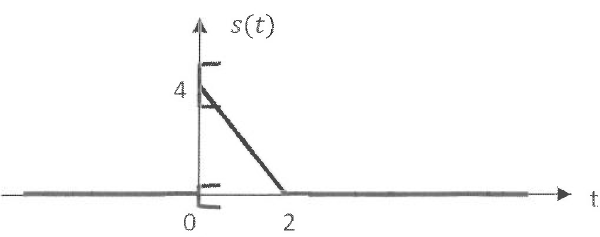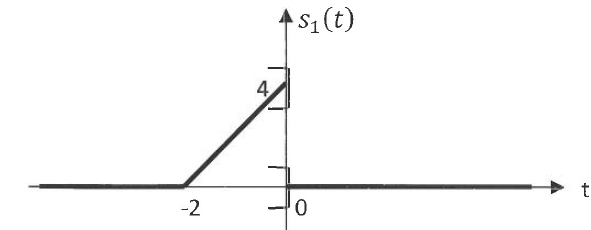
Mathématiques, concours ingénieur IESSA  2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Partie 1. On considère le signal s(t) ci-dessous : Q1. L'expression de s(t) est donnée par : s(t) =0 si t < 0. s(t) = -2t+4 si 0 < t < 2. s(t) = 0 si t > 2. Réponse E. Q2. On représente graphiquement s(-t) par : s1(t) =s(-t) = 2t+4 si -2 < t < 0 sinon 0. Réponse D. Q3. On représente la fonction g(t) = s(t) +s(-t). g(t) = 2t+4  si -2 < t < 0 ; g(t) = -2t+4 si 0 < t < 2 sinon 0. 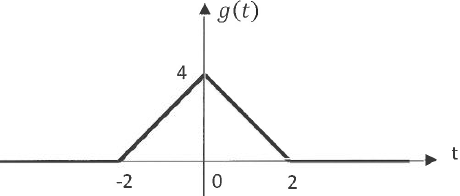Réponse D. Q4. A La fonction g(t) est paire car sa courbe représentative est symétrique par rapport à l'axe des ordonnées. Vrai. B La fonction g(t) est paire car sa courbe représentative est symétrique par rapport à l'axe des ordonnées. Faux. C. La fonction g(t) est paire car g(-t) = g(t). Vrai. D. La fonction g(t) est paire car g(-t) = -g(t). Faux. . Q5. On rapelle que la définition de la transformée de Fourier H(f) d'un signal h(t) est donnée par : 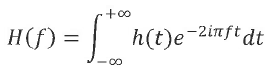A. Pour un signal h(t) pair, on peut écrire : 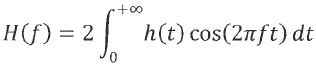vrai D.  Pour un signal h(t) impair, on peut écrire : 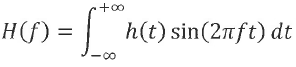vrai Q6. On considère le signal s2(t) ci-dessous. 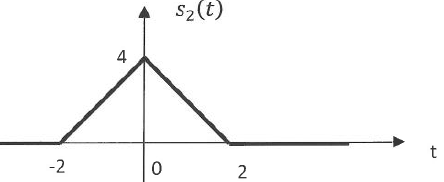Le calcul de la transformée de Fourier donne : Cette fonction est paire : pour t appartenant à [0 ; 2], s2(t) =4-2t ; pour t >2 : s2(t) = 0. 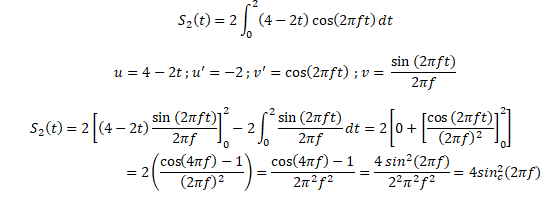Réponse C. Q7. Le spectre de s2(t) est alors : 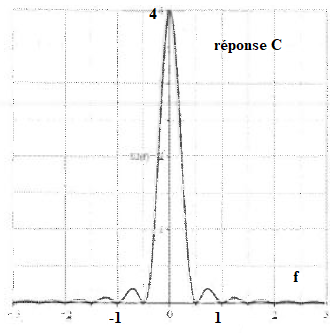Q8. 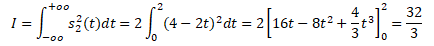On considère l'intégrale  : Réponse A. Partie II.  On considère deux nombres complexes z1 = x1+iy1 avex x1 un réel strictement positif et y1 un réel quelconque. z2 = r2 exp(-iq2) avec r2 réel strictement positif. Q9. La partie réelle de z3 = z1* z2 est  : z2 = r2(cos (q2) + i sin(q2)). Partie réelle de z3 : x1r2 cos (q2)-y1r2 sin (q2). Réponse E. Q10. Un argument de z4 = z1 / z2 est : arg(z1)-arg(z2)=arctan( y1/x1) -q2. Réponse B. Q11. Le module de z5 = z2+z1 est : z2 = r2(cos (q2) + i sin(q2)). z5 = x1+ r2 cos (q2) +i[y1+ r2 sin (q2)]. |z5| 2=(x1+ r2 cos (q2))2 +(y1+ r2 sin (q2))2. |z5| 2=x12+ r22 cos2 (q2) +2x1 r2 cos (q2) +y12+ r22 sin2 (q2) +2y1 r2 sin (q2) . |z5| 2=x12+ r22  +2x1 r2 cos (q2) +y12+ 2y1 r2 sin (q2) . Réponse C. Q12. Le module de z6 = exp(z1) est : z6 = exp(z1) =exp(x1+iy1) =exp(x1) * exp(iy1). exp(x1) est un réel ; le module de exp(iy1) vaut 1. |z6| =exp(x1) réponse B. ... .... Partie III. On considère l'équation différentielle suivante avec a non nul : y" +y'+ay = sin(2t). Q13. L'équation caractéristique associée admet comme solutions réelles : r2+r+a=0 : discriminant : 12-4a >0 si a < 1 /4. r1 = (-1+(1-4a)½) / 2 et r1 = (-1-(1-4a)½) / 2. Réponse D. Q14. La solution de l'équation différentielle sans second membre est : y = A exp(r1x) + B exp(r2x) avec A et B des constantes réelles si a < 1 /4. y = exp(-0,5t) [C cos (((4a-1)/2)½t) + D sin (((4a-1)/2)½t)] avec C et D des constantes réelles si a >0,25. Réponse D. Q15. On suppose que a = 2. Une solution particulière de l'équation différentielle est : On cherche une solution de la forme : y= A cos(2t) + B sin(2t). y' = -2Asin(2t) +2B cos(2t). y" =-4A cos(2t) -4B sin(2t) y"+y'+2y = (-4A+2B +2A) cos(2t)+(-4B-2A+2B) = sin(2t). 2(B-A)cos(2t)-2(A+B) =sin(2t). On identifie :-2(A+B) = 1 et  B-A = 0. A = B = -1/4. y= -1/4 cos(2t) -1/4 sin(2t). Réponse C. Q16. On suppose que a = 2. On cherche une solution de l'équation différentielle qui vérifie y(0) =0 et y'(0)=0. exp(0) = 1. Les termes en sinus sont nuls ; les termes en cosinus sont égaux à 1. y(t) = exp(-0,5t) [0,25 cos ((7½/2)t)+5*7½ / 28 sin( ((7½/2)t))]-0,25 sin(2t) -0,25 cos(2t)] peut convenir. y(t) = exp(-0,5t) [cos ((7½/2)t)+5/7½  sin( ((7½/2)t))]- sin(2t) - cos(2t)) peut convenir. On dérive : y(t) = exp(-0,5t) [0,25 cos ((7½/2)t)+5*7½ / 28 sin( ((7½/2)t))]-0,25 sin(2t) -0,25 cos(2t)] y'(t) = -0,5 exp(-0,5t)[0,25 cos ((7½/2)t)+5*7½ / 28 sin( ((7½/2)t))]+exp(-0,5t)[-0,25*7½/2 sin ((7½/2)t)+5*7½ / 28*7½/2 cos( ((7½/2)t))]-0,5cos(2t)+0,5 sin(2t). y'(0) =-0,5 *0,25+5*7½ / 28*7½/2-0,5 diffère de zéro. La réponse C ne convient pas. On dérive y(t) = exp(-0,5t) [cos ((7½/2)t)+5/7½  sin( (7½/2)t))]- sin(2t) - cos(2t)) y'(t) = exp(-0,5t) [-7½/2sin ((7½/2)t)+5/7½ *7½/2 cos( ((7½/2)t))]-0,5exp(-0,5t)[cos ((7½/2)t)+5/7½  sin( (7½/2)t))]-2cos(2t) +2sin(2t). y'(0) =5/7½ *7½/2 -0,5 -2=0 est vérifié. Réponse D. Partie IV. On considère la fonction f définie sur ]-oo ; -1] par f(t) = (t+1) / (2t2-t-1). Calcul de f '(t) en posant u = t+1 et v = 2t2-t-1 ; u' =1 ; v' =4t-1. (u'v-v'u) / v2 =[2t2-t-1-(4t-1)(t+1)]  / (2t2-t-1)2= (-2t2-5t) / (2t2-t-1)2. La dérivée s'annule pour t = -2,5 sur ]-oo ; -1]. f '(t) < 0 sur ]-oo ; -2,5[ et f(t) est décroissante. f '(t) > 0 sur ]-2,5 ; -1] et f(t) est croissante. Q17. Réponse D. La fonction est décroissante sur ]-oo ; -2]. Q18. La décomposition en éléments simples dans R de f(t) s'écrit :   2t2-t-1 = (t-1) (2t+1). f(t) = A /(t-1) + B /(2t+1). Réduire au même dénominateur :[A(2t+1) + B(t-1) ] / [(t-1) (2t+1)]. Identifier les numérateurs : 2At+A+Bt-B = t+1. 2A+B = 1 : A-B = 1. 3A = 2 ; A = 2 /3 et B = -1/3. f(t) = 2 /(3(t-1)) -1 /(3(2t+1)). Réponse D. Q19. Le calcul de l'intégrale suivante donne : Réponse B. Q20. L'intégrale généralisée B. Converge car f(t) tend vers zéro quand t tend vers moins l'infini. Vrai. L'aire comprise entre la courbe et les axes est finie.

menu