Densimètre, sphère chargée, concours interne ingénieur IEEAC et ICNA 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... On modélise le densimètre par une tige cylindrique de rayon a, de hauteur H et d’une boule lestée de rayon R. L’ensemble présente une masse m. Lorsque le densimètre est plongé dans un liquide au repos de densité d, une certaine hauteur h dépasse du liquide. On peut alors lire directement la densité sur l’échelle graduée. 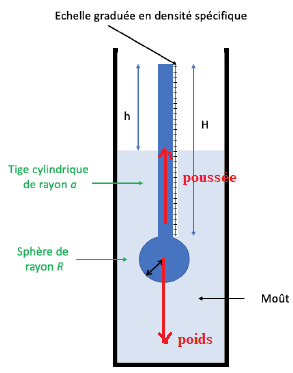On désire ici faire le lien entre h et d On note g l’accélération de pesanteur. Pour les applications numériques on prendra : a = 5 mm, H = 30 cm, R = 2 cm, g = 10 m.s-2 et m = 20 g. Q1) Exprimer le volume V, la masse volumique r0 et le poids P du densimètre en fonction des paramètres du modèle. Calculer la densité d0 du densimètre. V = 4 / 3 p R3 +pa2H=4 / 3 x3,14 x0,023 +3,14 x0,0052 x0,30 =3,35 10-5 +2,36 10-5 =5,7 10-5 m3. r0  = m / V = 0,020 / (5,7 10-5) ~350 kg m-3. P = m g = 0,020 x10 = 0,20 N.. d0  = r0  / reau =350 / 1000 = 0,35. Q2) Énoncer le théorème d’Archimède. Un corps immergé dans un fluide (liquide ou gaz), subit de la part du fluide des forces dont la résultante est : verticale vers le haut appliquée au centre du volume de liquide déplacé norme : volume liquide déplacé(m3)* masse volumique du liquide(kgm-3)*9,8 Q3) Quelle est la masse volumique de l’eau re et de l’air ra ? Justifier que l’on puisse négliger l’action de l’air. re =1000 kg m-3 ;  ra =1,3 kg m-3~ re /800. La masse volumique de l'air étant très inférieure à celle de l'eau, l'action de l'air est négligeable. Q4) Le densimètre flotte dans le moût de masse volumique rm . Exprimer la poussée d’Archimède  en fonction de rm, g, V, h et a. Fm =rm g [4 / 3 p R3 +pa2(H-h)]. Fm =rm g (V -pa2h). Q5) On plonge le densimètre dans de l’eau à 20°C. On note h0 la hauteur immergée. Faire un schéma détaillé avec les différentes forces appliquées, leurs points d’application et la hauteur h0. Le densimètre est en équilibre sous l'action de son poids ( appliqué au centre de gravité) et de la poussée d'Archimède ( appliquée au centre du volume d'eau déplaccé) P = m g ;  Feau =re g [4 / 3 p R3 +pa2h0]=re g [4 / 3 p R3 + pa2H -pa2H+pa2h0]=re g [V -pa2H+pa2h0]. Quelle est la lecture de la densité spécifique ? La densité spécifique de l'eau est égale à 1000. Quelle est l’importance de la boule lestée ? Le centre de gravité étant très en dessous du centre de poussée, le densimètre reste vertical. Q6) Établir la relation reliant h, h0, rm, r0 et re. En déduire la relation reliant h- h0 à la densité dm du moût, la densité d0 du densimètre et à h0. Commenter le résultat précédent par rapport à la nature de l’échelle. Feau =re g [V -pa2H+pa2h0] = poids du densimètre. Fm=Feau =poids du densimètre. re  [V -pa2H+pa2h0] = m=r0V. V -pa2H+pa2h0 =r0 / reV. pa2h0 = V(r0 / re-1)+pa2H. h0 = V(r0 / re-1)/ (pa2) +H. rm  (V -pa2h)= m=r0V. V -pa2h =r0 / rm V. pa2h =V(1-r0 / rm ). h =V(1-r0 / rm )/ (pa2). 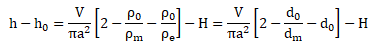Plus il y a de sucre dans le moût, moins le densimètre s'enfonce et vice-versa. Q7) On effectue un développement limité de dm. On pose dm=1+d. Montrer que h- h0=d0h0d /(1-d0). Commenter. Si on prend h0 = 2 cm, calculer h dans le cas de la photo de la figure c ( densité spécifique 69). Ce résultat vous semble-t-il cohérent ? ... .... Electrostatique. On considère en régime stationnaire une répartition de charges à symétrie sphérique de centre O, de charge volumique r(M,t)=r(r) inconnue pour r appartenant à [0, R] avec R une constante. Sur [R, +∞[ , on a du vide. A partir de mesures du champ électrique, on désire trouver l’expression de la charge volumique locale et la charge totale contenue dans la sphère de rayon R. I Généralité. Q1) En statique, rappeler les deux équations de Maxwell locales vérifiées par le champ électrique E(M) et préciser leurs noms. Q2) Comment se nomme la constante qui apparaît dans l’une des équations précédentes ? Quelle est son unité ? Quelle est sa valeur ? L'équation de Maxwell-Gauss conduit au théorème de Gauss : le flux du champ électrique à travers une surface fermée est égale au produit  de la charge intérieure contenue dans le volume V délimité par cette surface et la permitivité du vide Qint / e0. ( e0 ~10-11 F m-1). La divergence du champ électrique est proportionnelle à la distribution de charges électriques. Le champ électrique autour d'une charge est donc comme un oursin, où les épines constituent les lignes de champ partant du centre et divergeant vers l'infini. Equation de Maxwell - Faraday : la loi de Faraday s'écrit : e = -dF / dt  ( e ; fem induite ; F flux du champ magnétique. Le rotationnel du champ électrique est proportionnel à la variation du champ magnétique au cours du temps. Q3) Quelle propriété sur le champ électrique E peut-on déduire de l’autre équation ? Montrer qu’il apparaît une fonction scalaire V(M). La conservation du flux magnétique implique que le champ magnétique est un champ rotationnel. Q4) Par une étude rigoureuse, montrer que le champ électrique peut se mettre sous la forme Il y a invariance de la distribution de charges pour toute rotation autour de O, donc E ne dépend ni de q, ni de f. Pour la suite de l’exercice, on prendra : E(r)=E0 sur [0, R] E(r)=E0R2/r2 sur [R, +∞[ où E0 est une constante positive. II Potentiel. La distribution de charges étant finie, on impose par convention que : V(r) =0 à l'infini. Q5) Établir l’équation différentielle reliant V(r) à E(r). E(r) = - dV(r) / dr. Q6) Résoudre cette équation dans les deux domaines de définition. Sur [R, +∞[  : E0R2/r2 = -dV /dr ; intégrer entre r et +oo :  V(r) = E0R2/ r (1). Sur [0, R] : E0 = -dV/dr ; intéger : V(r) = -E0 r + cste. (2). Continuité du potentiel (1) donne : V(R ) = E0R. Repport dans (2) : -E0R + cste= E0R ; Cste = 2 E0R. V(r) = -E0 r + 2 E0R. Q7) Tracer avec soin l’allure de V(r). III. Charge. Afin de trouver la charge volumique locale, nous allons effectuer un bilan de charges. Q8) Quelle est la charge contenue dans une couche sphérique de centre O comprise entre les sphères de rayon r et r + dr ? Sphère extérieure de rayon r +dr : Q1 = r 4/ 3 p (r+dr)3. Sphère intérieure de rayon r : Q2 = r 4/ 3 p r3. Charge contenue dans une couche sphérique de centre O  : Q1 -Q2 = r 4/ 3 p [ (r+dr)3- r3]. Q =Q1 -Q2 = r 4/ 3 p [ 3r2dr +3r dr2+dr3]. En éliminant les termes du deuxième ordre et plus : Q = r 4 p r2dr. Q9) A l’aide du théorème de Gauss dont vous rappellerez l’énoncé, montrer que : Le flux du champ électrique sortant d'une surface fermée est proportionnel à la charge électrique totale contenue dans le volume V délimité par cette surface. La constante de proportionalité est 1 / e0. Q10) Déterminer r(r). E(r)=E0 sur [0, R] ; Surface de Gauss : sphère de rayon r. Flux : 4pr2E0 =4 /3 p r3 r / e0. r = 3E0 e0 / r. Q11) Tracer avec soin r(r). Q12) Quelle est la charge totale Q0 contenue dans la sphère de rayon R ? Q0 = r 4/3 p R3. Q13) Établir que, pour r supérieur à R, le champ créé par la distribution de charges est équivalent à celui d’une charge ponctuelle Q0 placée en O. Flux du champ électrostatique sortant d'une sphère de rayon r : E(r) 4 p r2. Charge totale contenue dans la sphère de rayon R : Q = 4 / 3 p R3 r. Le théorème de Gauss conduit à : E(r) = Q /(4 p e0 r2). Ce champ est identique à celui créé par une charge ponctuelle Q qui serait placée au centre de la sphère.

menu